Погрузимся в увлекательный мир статистики, где каждое число и каждая цифра имеет свое значение. Сегодня мы поговорим о важных понятиях, которые лежат в основе понимания доверительных интервалов. Но не спешите проникаться тоской от предполагаемой сложности, ведь у нас есть верный путеводитель – абсолютная и относительная погрешность.
Ловкость рук и точность разума – вот квинтэссенция науки о погрешностях. Абсолютная и относительная погрешности представляют из себя незаменимые инструменты в анализе данных и принятии верных решений. Но не стоит путать их с обычными ошибками или совсем случайными неточностями. Эти понятия исследуют и отражают систематические различия между фактическими наблюдениями и теоретическими ожиданиями.
Любопытно, что абсолютная и относительная погрешности не являются противоположными понятиями, а, на самом деле, взаимосвязанными показателями, которые дополняют друг друга. Абсолютная погрешность измеряет точность наблюдаемого значения в его самых реальных границах, а относительная погрешность позволяет узнать "на сколько" это наблюдаемое значение отклоняется от истинного значения, давая представление о его относительной величине.
Измерения и ошибки: понятие абсолютной неточности

Абсолютная неточность представляет собой абсолютное значение разницы между измеренным значением и настоящим значением измеряемой величины. Она позволяет оценить масштаб ошибки и понять, насколько точные результаты наших измерений.
Однако, следует отметить, что абсолютная неточность сама по себе не позволяет определить точность измерений. Чтобы иметь представление о точности, нам необходимо знать также величину измеряемой величины и ее колебания. Например, если мы измеряем длину линейки с точностью до 1 миллиметра, а абсолютная неточность составляет 0,5 миллиметра, то результат измерения будет достаточно точным. Однако, если измеряемая величина имеет большие колебания, а абсолютная неточность также высока, это говорит о необходимости использования более точного метода измерения или повторного измерения с большей точностью.
Определение и примеры убыточности величины

Когда мы изучаем понятие убыточности величины, мы фокусируемся на его значении и примерах, чтобы лучше понять его сущность и применение в различных областях. Убыточность величины представляет собой меру неопределенности или неточности значения, которое мы измеряем или оцениваем. Она указывает на то, насколько далеко могут быть наши измерения или оценки от истинного значения.
Пример 1:
Допустим, у вас есть прибор, который измеряет температуру воздуха в определенном помещении. Вы проводите серию измерений и получаете разные значения: 20°C, 19.5°C, 20.2°C, 19.8°C и т. д. Однако, истинное значение может быть, например, точно 19.7°C. Разница между этим истинным значением и вашими измерениями является абсолютной погрешностью.
Пример 2:
Представьте, что вы оцениваете вес яблока, используя весы, которые показывают до одной десятой грамма. Ваше измерение показывает 150.3 грамма. Однако, на самом деле, вес яблока может быть точно 150 грамм. Разница между вашим измерением и истинным значением является абсолютной погрешностью.
Таким образом, понимание абсолютной погрешности помогает нам оценить точность и надежность наших измерений или оценок. Ее значение будет зависеть от контекста и применения, поэтому важно учитывать абсолютную погрешность при работы с числовыми значениями в любой области.
Оценка точности: основы относительной неточности
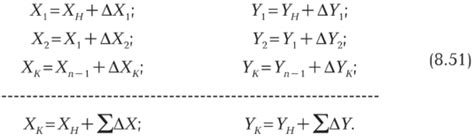
При проведении оценки точности важно учитывать не только абсолютную, но и относительную неточность. Если абсолютная погрешность показывает, насколько измеренное значение отклоняется от истинного значения, то относительная погрешность позволяет оценить эту неточность в процентах или в отношении к измеренному значению.
Понимание основ относительной неточности является важной частью процесса оценки точности измерений. Относительная погрешность позволяет сравнивать измерения, произведенные различными инструментами или в разных условиях.
- Относительная неточность может быть выражена в процентах, показывая долю погрешности от измеренного значения.
- Другой способ выразить относительную погрешность - в виде отношения между абсолютной погрешностью и измеренным значением.
- Относительная погрешность используется для сравнения результатов измерений и выбора наиболее точного измерительного метода.
Правильная интерпретация и оценка относительной погрешности позволяет точно оценить степень точности измерений и принять правильные решения на основе полученных результатов.
Понятие относительной погрешности и способы ее расчета

Для расчета относительной погрешности существует несколько способов. Один из них - использование формулы относительной погрешности, которая выражает отношение абсолютной погрешности к измеряемой величине. Эта формула позволяет получить числовое значение относительной погрешности.
Еще один способ расчета относительной погрешности - сравнение значений различных измерений или расчетов с заданным стандартом или эталоном. Путем сопоставления полученных результатов с эталоном можно определить разницу между ними и вычислить относительную погрешность.
Относительная погрешность может быть выражена в процентах, долях или других единицах измерения, в зависимости от контекста и типа данных. Этот показатель позволяет учесть вариативность и случайные факторы, которые влияют на точность результатов. Чем меньше относительная погрешность, тем более точными и надежными являются измерения или расчеты.
Влияние точности на уровень доверия интевала
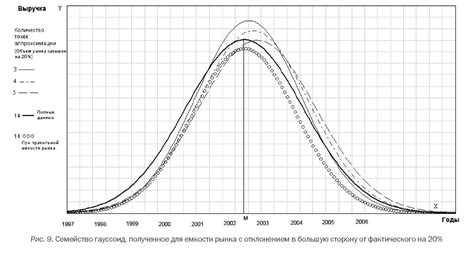
Когда мы строим доверительный интервал, важно учитывать точность исходных данных, поскольку она существенно влияет на уровень доверия интервала.
Точность отражает степень уверенности в полученных результатах и зависит от различных факторов, таких как размер выборки, ошибки измерений и метода статистического анализа. Чем точнее данные, тем меньше вероятность того, что доверительный интервал содержит истинное значение параметра.
Важно понимать, что точность необходимо учитывать при интерпретации доверительного интервала. Если мы имеем низкую точность, то возможно, что наш интервал будет широким и содержит много значений, что делает его более ненадежным. Если же точность высокая, то интервал будет уже и содержит меньшее число возможных значений.
| Низкая точность | Высокая точность |
| Большой интервал | Узкий интервал |
| Много возможных значений | Мало возможных значений |
| Меньшая уверенность в результатах | Большая уверенность в результатах |
Влияние абсолютной и относительной неточности на расчеты интервала доверия
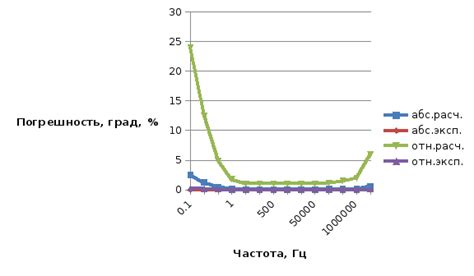
В контексте изучения погрешностей и интервалов доверия, крайне важно понимать, как абсолютная и относительная неточность могут повлиять на результаты расчетов. Погрешности могут возникнуть в результате неточности или случайных факторов при сборе данных, оценке или прогнозировании. При расчете интервалов доверия, эти погрешности играют ключевую роль в определении точности и надежности полученных значений.
Абсолютная неточность отражает фактическое отклонение между измеренными или оценочными значениями и их истинными значениями. Она представляет собой конкретное числовое значение, выражающее абсолютное расстояние между двумя точками. Относительная неточность, с другой стороны, измеряет отклонение в процентном соотношении по отношению к измеренному или оцененному значению. Этот вид неточности предоставляет информацию о том, насколько большим или малым является отклонение в относительном сравнении.
Наличие абсолютной или относительной погрешности может значительно влиять на расчеты интервалов доверия. В случае больших значений абсолютной или относительной неточности, интервалы доверия могут быть широкими, что означает, что полученные результаты имеют большую неопределенность и меньшую точность. Напротив, меньшие значения неточности указывают на более узкие интервалы доверия и большую точность. Понимание влияния абсолютной и относительной неточности на расчеты интервалов доверия помогает исследователям и аналитикам принимать во внимание факторы погрешности и определять эффективные стратегии сбора и анализа данных.
Таким образом, учет абсолютной и относительной неточности играет важную роль в доверительных интервалах и позволяет оценить точность и надежность полученных результатов. Понимание различий между этими видами погрешностей помогает исследователям более точно интерпретировать результаты и осуществлять информированные решения на основе полученных данных.
Вопрос-ответ

Что такое абсолютная погрешность доверительного интервала?
Абсолютная погрешность доверительного интервала - это разница между средним значением выборки и пределами интервала с учетом уровня доверия. Она показывает насколько значения выборки могут отклоняться от истинного значения с учетом доверительного уровня.
Чем отличается относительная погрешность доверительного интервала от абсолютной?
Относительная погрешность доверительного интервала выражается в процентах и показывает отношение абсолютной погрешности к среднему значению выборки. В отличие от абсолютной погрешности, она позволяет сравнивать погрешности для разных выборок с разными средними значениями.
Какая разница между абсолютной и относительной погрешностями доверительного интервала?
Основная разница между абсолютной и относительной погрешностями доверительного интервала заключается в способе представления. Абсолютная погрешность выражается в единицах измерения и показывает разницу между средним значением выборки и пределами интервала. В то же время, относительная погрешность выражается в процентах и позволяет сравнивать погрешности для разных выборок, учитывая их средние значения.