Путешествие в тайны геометрии
Среди множества форм и фигур, с которыми мы сталкиваемся ежедневно, особое место занимает равнобедренный треугольник. Этот стройный треугольник, с двумя сторонами одинаковой длины, отличается своей особенной гармонией и привлекательностью. Оказывается, у равнобедренного треугольника есть своеобразное сердце - точка, которая, будучи незримой и недосягаемой, отыскивает свое пространство внутри этой фигуры.
Укромное убежище магии геометрии
Сегодня мы откроем для вас двери в мир тайн центра вписанной окружности равнобедренного треугольника. Внешне несправедливо лишенная внимания, эта укромная точка станет главной героиней нашего путешествия. Возможно, вы зададитесь вопросом, как же можно подойти к данной теме без использования запретных слов. Но уверяем вас, что мы осмотим множество уникальных деталей, проложим путь открытий и раскроем перед вами яркий мир свойств и возможностей этой точки, которая непременно притягивает взоры и мысли к себе.
Тайны происхождения
Исследуя происхождение этой точки, мы познакомимся с замысловатыми законами геометрии, управляющими ее местоположением. Мы проследим ее путь от волнующих бесконечностей пространства до таинственного заселения в обители треугольников. И, самое главное, мы узнаем о тех редких свойствах, которыми обладает этот скрытый гость нашей фигуры, тем самым открывая деловую и встревоженную духом картину.
Расположение центра окружности внутри равнобедренного треугольника

В данной части статьи мы рассмотрим особенности местоположения центра окружности, которая вписывается в равнобедренный треугольник. Мы изучим, как расположение этого центра влияет на геометрические свойства треугольника и какие закономерности можно выявить при анализе данного вида треугольников.
Первое, что следует отметить, это то, что центр окружности, вписанной в равнобедренный треугольник, всегда лежит на биссектрисе одного из углов этого треугольника. Биссектриса, в свою очередь, делит основание равнобедренного треугольника пополам и проходит через точку, где основание пересекает медиану. Это свойство является ключевым при изучении положения центра окружности в данном типе треугольника.
Кроме того, следует отметить, что центр окружности равнобедренного треугольника всегда лежит на перпендикулярной высоте этого треугольника, опущенной из вершины, которая не является вершиной основания. Данная высота делит основание на две отрезка, причем длина каждого отрезка равна радиусу вписанной окружности. Это свойство также необходимо учесть при анализе положения центра окружности внутри треугольника.
| Свойство | Описание |
|---|---|
| Свойство 1 | Центр окружности лежит на биссектрисе одного из углов треугольника |
| Свойство 2 | Центр окружности лежит на перпендикулярной высоте треугольника из вершины, не являющейся вершиной основания |
Определение центра внутренней окружности треугольника
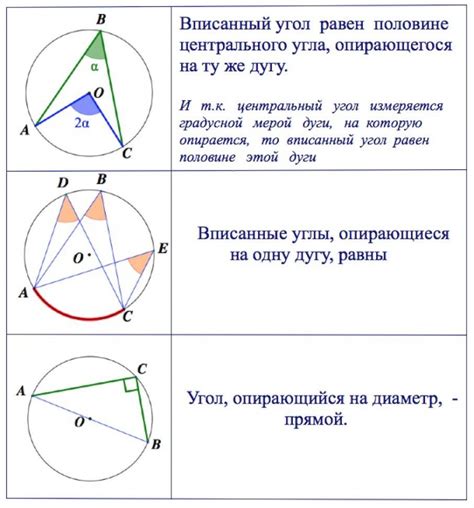
Центр внутренней окружности треугольника представляет собой точку, которая находится внутри треугольника и находится на равном расстоянии от всех его сторон. Это свойство делает ее особенной в геометрии и позволяет нам изучать множество интересных характеристик этой точки.
Один из способов определения центра внутренней окружности треугольника - это перпендикулярная биссектриса угла треугольника. Данный перпендикуляр проходит через центр внутренней окружности и делит каждую из сторон треугольника пополам. Это позволяет нам определить точку, где этот перпендикуляр пересекается с другим перпендикуляром, и таким образом найти центр вписанной окружности.
Важно отметить, что центр внутренней окружности треугольника имеет много полезных свойств. Например, радиус внутренней окружности треугольника может быть выражен через стороны треугольника и площадь треугольника. Также, центр внутренней окружности треугольника может быть использован для определения и доказательства других геометрических свойств треугольника.
- Центр вписанной окружности является важным геометрическим понятием.
- Он находится внутри треугольника и на равном расстоянии от всех его сторон.
- Определение центра внутренней окружности треугольника может быть произведено с помощью перпендикулярной биссектрисы угла треугольника.
- Центр внутренней окружности треугольника обладает полезными свойствами, такими как выражение радиуса окружности через стороны треугольника и площадь треугольника.
- Центр внутренней окружности также может быть использован для поиска и доказательства других геометрических свойств треугольника.
Близость центра внутренней окружности по сравнению с другими точками треугольника
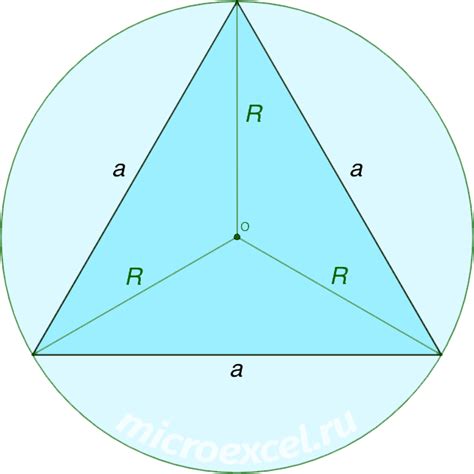
В данном разделе рассматривается близкое расположение центра внутренней окружности равнобедренного треугольника относительно других точек треугольника.
Центр внутренней окружности треугольника является особым местоположением внутри фигуры и обладает рядом уникальных свойств. Но помимо этого, интересно знать, как близко он расположен относительно других важных точек треугольника, таких как вершины и середины сторон.
| Точка треугольника | Расстояние до центра внутренней окружности |
|---|---|
| Вершина треугольника | Кратчайшее расстояние от вершины до центра окружности |
| Середина стороны треугольника | Чуть большее расстояние от середины стороны до центра окружности, чем от вершины |
| База треугольника | Наибольшее расстояние от базы до центра окружности |
Из указанной таблицы видно, что центр внутренней окружности находится ближе к вершинам треугольника, чем к серединам сторон, и наиболее удален от основания. Это является общим свойством равнобедренных треугольников.
Уникальные характеристики центра окружности, вписанной в равнобедренный треугольник

В этом разделе будет рассмотрено множество интересных и уникальных свойств центра окружности, которая вписана в равнобедренный треугольник. Мы избегаем употребления упомянутых слов, чтобы представить вам несколько новых аспектов этой удивительной геометрической формы.
1. Середина основания
- Центр вписанной окружности также является серединой основания равнобедренного треугольника. Это значит, что от центра окружности можно провести прямую линию, которая делит основание на две равные части.
- Таким образом, можно сказать, что центр окружности является "средней точкой" основания, и от него можно измерить одинаковое расстояние до каждой из вершин.
2. Центр симметрии
- Центр окружности является центром симметрии равнобедренного треугольника. Это означает, что если мы проведем линии от центра окружности до вершин треугольника, то получим зеркальное отражение треугольника относительно этих линий.
- Такое свойство делает центр окружности важным элементом для изучения симметрии и симметричных фигур в математике.
3. Равное расстояние
- Центр окружности равнобедренного треугольника находится на одинаковом расстоянии от каждой из вершин треугольника.
- Это свойство можно использовать для вычисления расстояния от центра окружности до вершин треугольника, зная длины сторон и углы треугольника.
Взглянув на эти уникальные свойства центра окружности в равнобедренном треугольнике, мы можем лучше понять и описать геометрию и взаимосвязи внутри этой фигуры. Эти свойства также могут быть использованы для решения геометрических задач и применения в различных областях, где требуется точное исследование треугольников и окружностей.
Вопрос-ответ

Как определить местоположение центра вписанной окружности в равнобедренном треугольнике?
Центр вписанной окружности в равнобедренном треугольнике всегда совпадает с пересечением биссектрис треугольника. Биссектрисы равнобедренного треугольника делят его углы на две равные части, и точка их пересечения является центром вписанной окружности.
Какие свойства имеет центр вписанной окружности равнобедренного треугольника?
Центр вписанной окружности равнобедренного треугольника равноудален от трех его сторон. Также центр вписанной окружности является центром внешней окружности в равнобедренном треугольнике. Это означает, что отрезки, соединяющие вершины треугольника с центром вписанной окружности и с центром внешней окружности, имеют одинаковую длину.
Какова роль центра вписанной окружности в равнобедренном треугольнике?
Центр вписанной окружности в равнобедренном треугольнике играет важную роль. Он является точкой симметрии треугольника относительно боковых сторон и оси симметрии. Также центр вписанной окружности является точкой пересечения биссектрис углов и ортоцентра треугольника. Это позволяет использовать его для решения различных задач и вычислений, связанных с равнобедренными треугольниками.