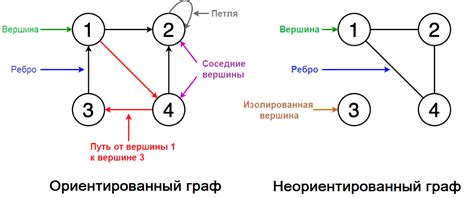
Когда мы исследуем мир сложной структуры, обнаруживаем, что множество явлений и процессов могут быть представлены в виде графов. Граф - это абстрактная модель, которая позволяет нам изучать взаимосвязи и связанность между объектами. Внутри действительно могущественной и непостижимой сети графов, одной из самых удивительных и фундаментальных конструкций является цикл.
Цикл - это уникальное и повторяющееся явление. В мире графов оно представляет собой замкнутую цепь, образованную ребрами, которая возвращает нас в исходную точку. Циклы могут быть простыми и сложными, они могут состоять из трех или более вершин, образуя непредсказуемые и запутанные структуры. Знание и понимание принципов и свойств циклов в графах играет важную роль в разных областях, от компьютерных наук до социологии и биологии.
Погрузиться в удивительный мир циклов в графах - значит расширить свой кругозор и понять их непосредственное влияние на реальные явления. Изучение принципов циклов позволяет нам понять, как они могут использоваться для моделирования и прогнозирования различных процессов. Каждый цикл имеет свои уникальные свойства и характеристики, которые позволяют нам изучать различные состояния системы и применять их в практических целях.
Определение и ключевые понятия в контексте цикла графа

Рассмотрение цикла графа включает в себя ряд основных понятий и определений, которые позволяют более глубоко понять эту концепцию. На этом этапе мы представим общую идею раздела, не углубляясь в конкретные определения и формальности.
Исследование и анализ цикла графа являются фундаментальной задачей в теории графов. Цикл, в данном контексте, представляет собой замкнутую последовательность вершин в графе, где каждая вершина связана с предыдущей и следующей по определенным правилам. Важными аспектами, связанными с циклами графа, являются их длина, структура и наличие особых свойств.
- С точки зрения структуры, циклы могут быть простыми или сложными. Простые циклы представляют собой замкнутые пути без повторяющихся вершин или ребер. В то время как сложные циклы могут содержать повторения и перекрестные связи.
- Длина цикла определяется количеством вершин или ребер, составляющих замкнутую последовательность. Эта характеристика играет важную роль при анализе графов и определении их свойств.
- Цикл может быть как обнаружен в заданном графе, так и создан путем соединения различных вершин и ребер. Анализ этих процессов важен для понимания формирования и динамики циклов графа.
- Особенности циклов графа могут включать наличие дополнительной информации о вершинах, ребрах или связях, которая может использоваться для классификации или описания их поведения и свойств.
В следующих разделах мы подробно рассмотрим каждый из этих аспектов и изучим принципы и свойства циклов графа, которые играют ключевую роль в их анализе и применении.
Основной каркас графа: история его пути повторений

Цикл в графе – это феномен, который отображает путь обратно к точке отправления, через некоторые другие вершины. Он образуется, когда из одной вершины можно снова попасть в нее же, последовательно проходя через другие вершины.
Такой цикл может быть рассмотрен как замкнутая история, где каждый шаг, каждая ветвь, каждая возвратная дуга являются важными элементами для понимания графа в целом. Циклы в графах предоставляют нам ценную информацию о потенциальных путях и соединениях между различными вершинами.
Важно понимать, что циклы не являются однозначным свойством графа, а скорее его основным каркасом. Каждый граф может содержать разные циклы, которые отражают его уникальные характеристики и связи. Изучение циклов позволяет нам погрузиться в историю графа, понять его развитие и потенциал для обратных связей и повторных визитов.
- Цикл в графе – это путь, который возвращает нас к начальной точке через другие вершины.
- Циклы являются фундаментальной особенностью графовой структуры.
- Циклы в графах содержат в себе важную информацию о возможных путях и соединениях.
- Циклы являются элементами истории графа – каждый шаг и возвратная дуга имеют свое значение в понимании этой истории.
Основные понятия связанные с циклами в графе

В изучении циклов в графах, существует набор ключевых терминов и понятий, которые помогают нам понять и анализировать данную структуру. Эти термины и понятия придают нам возможность описывать свойства и особенности циклических структур без прямого использования вышеупомянутых слов.
Когда мы рассматриваем графы, мы исследуем не только их топологию и соединения между вершинами, но и свойства, которые возникают из наличия или отсутствия циклов. Например, существуют вершины, которые являются точками начала и конца циклов и мы можем описывать их в терминах "дуг", "путей" и "смежности". Они помогают нам понять направленность передвижения и циклическую природу графа.
Еще одним важным понятием является "длина петли", которая представляет собой количество вершин или ребер, через которые проходит цикл. Это позволяет нам оценивать сложность и размер циклических структур и сравнивать их с другими частями графа.
Анализ циклов также включает понятие "эйлерового цикла" и "гамильтонова цикла", которые отражают уникальные свойства графа. Эйлеров цикл проходит через каждое ребро графа только один раз, в то время как гамильтонов цикл проходит через каждую вершину ровно один раз. Эти циклы представляют собой особые комбинации построения путей, связывая все вершины и ребра графа.
Таким образом, основные понятия, связанные с циклами в графе, позволяют нам анализировать и описывать состав, размер, связь и уникальные свойства циклических структур. Использование этих терминов и понятий позволяет нам лучше понять функциональность и важность циклического представления данных в графах.
Алгоритмы поиска циклов в графе: принципы и стратегии
1. Метод поиска в глубину Один из самых простых и часто используемых методов для обнаружения циклов в графе - это алгоритм поиска в глубину. Этот метод основывается на идее о переходах от одной вершины к другим, пока не будет обнаружен цикл или будет достигнута конечная вершина. Используя стек для отслеживания пути, алгоритм поиска в глубину может эффективно найти все циклы в графе. |
2. Метод поиска в ширину Другой эффективный метод для поиска циклов в графе - это алгоритм поиска в ширину. В отличие от метода поиска в глубину, алгоритм поиска в ширину рассматривает все вершины на одном уровне, прежде чем переходить к следующему уровню. Это позволяет найти наименьший цикл (цикл минимальной длины), если таковой существует, и предоставляет более общий обзор всей структуры графа. |
3. Алгоритм Флойда-Уоршалла Алгоритм Флойда-Уоршалла, изначально разработанный для нахождения кратчайших путей в графе, также может быть использован для обнаружения циклов. Путем подсчета всех возможных путей между парами вершин, алгоритм Флойда-Уоршалла позволяет найти циклы любой длины в графе, в том числе и отрицательного веса. Однако этот метод может оказаться неэффективным для больших графов из-за высокой вычислительной сложности. |
Алгоритмы обнаружения циклических путей в структурах взаимосвязей
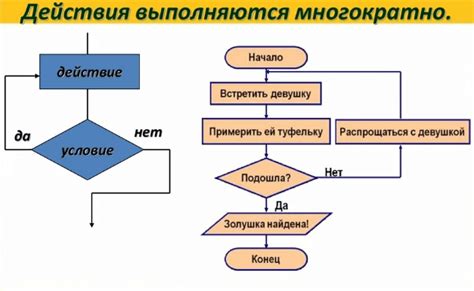
В данном разделе мы рассмотрим различные методы и алгоритмы, которые позволяют обнаруживать циклические пути в структурах взаимосвязей без прямого указания на само понятие "цикл" или "граф".
Еще один метод основывается на итеративном обходе структуры и проверке наличия обратных связей. Если в процессе обхода встречается вершина с уже установленным флагом "посещенная", то это говорит о наличии циклического пути в структуре. Такой алгоритм может быть использован для обнаружения циклов в деревьях, графах и других иерархических структурах.
| Метод | Принцип работы | Применение |
|---|---|---|
| Анализ повторяющихся элементов | Поиск повторений в последовательности данных | Журналы событий, базы данных, анализ временных рядов |
| Итеративный обход со связями | Проверка наличия обратных связей в процессе обхода | Деревья, графы, иерархические структуры данных |
Каждый из этих методов имеет свои преимущества и недостатки и подходит для разных типов структур и задач. Общей целью является обнаружение циклических путей, что может помочь в анализе взаимосвязей и выявлении потенциальных проблем или ошибок в системе.
Вопрос-ответ

Какие принципы лежат в основе цикла графа?
Основными принципами цикла графа являются замкнутость и постоянство количества вершин и ребер. Замкнутость означает, что граф представляет собой замкнутую фигуру, в которой нет никаких отрывков. Постоянство количества вершин и ребер означает, что при удалении или добавлении вершин или ребер, количество вершин и ребер всегда остается неизменным.
Какие свойства имеет цикл графа?
Цикл графа имеет несколько свойств. Во-первых, каждая вершина цикла имеет одну входящую и одну исходящую дугу. Во-вторых, цикл графа не содержит ациклических подграфов. В-третьих, цикл графа является простым, то есть не имеет повторяющихся вершин и ребер. Кроме того, цикл графа может быть ориентированным или неориентированным, в зависимости от наличия направления на ребрах.
Какие принципы позволяют определить наличие цикла в графе?
Определение наличия цикла в графе основывается на принципах обхода графа и проверки повторного посещения вершин. Одним из методов является алгоритм обхода графа в глубину (DFS), при котором посещение вершины записывается в стек. Если при обходе встречается вершина, которая уже есть в стеке, то это означает наличие цикла в графе.
Какую роль играют циклы в графах?
Циклы в графах играют важную роль и используются в различных областях. Например, они позволяют моделировать связи между объектами, определять циклические зависимости или циклические процессы. Кроме того, циклы позволяют находить оптимальные пути в графах, решать задачи коммивояжера, анализировать поведение алгоритмов и т.д.
Каким образом можно представить цикл графа?
Цикл графа можно представить различными способами. Например, с использованием матрицы смежности, где каждый элемент матрицы указывает наличие ребра между соответствующими вершинами. Также цикл графа можно представить списком смежности, где для каждой вершины указывается список вершин, с которыми она соединена ребрами. Кроме того, существуют и другие структуры данных, такие как инцидентная матрица или представление в виде графических диаграмм.



