Для многих людей математические операции являются чем-то волшебным и непонятным. Однако, существует несколько простых и эффективных способов найти число, обратное значению арифметического выражения. При помощи этих методов вы сможете легко справиться с задачами, требующими нахождения обратного числа.
Важно отметить, что процесс нахождения обратного числа может быть различным в зависимости от типа арифметического выражения. Но не беспокойтесь, мы рассмотрим самые распространенные сценарии и поделимся с вами лучшими методами. Будьте готовы к тому, чтобы освоить новые приемы и стратегии, которые помогут вам в быстром и точном определении обратного числа.
Умение находить число, обратное арифметическому выражению, является важной навыком и может быть полезной как в повседневной жизни, так и в профессиональной деятельности. Независимо от того, работаете ли вы в финансовой сфере, программировании или занимаетесь наукой, умение быстро находить обратное число позволит вам решать задачи более эффективно и точно.
Основные способы получения числа с обратным значением выражения

В данном разделе мы рассмотрим основные методы, которые позволяют найти число, обратное значению выражения, без использования сложных вычислительных алгоритмов. На протяжении многих лет математики и ученые исследовали различные подходы к нахождению обратного числа, и в результате были разработаны эффективные и простые в использовании методы.
Начнем с метода обратного умножения. Данный подход заключается в нахождении числа, которое при умножении на значение выражения даст единицу. Например, если имеется выражение "а * b", чтобы найти обратное число выражению, необходимо найти такое число x, при котором x * (a * b) = 1. Это можно сделать путем деления единицы на произведение a и b.
Следующий метод, который мы рассмотрим, называется методом обратной суммы. Он основан на идее нахождения числа, которое в сумме с выражением даст ноль. Например, если имеется выражение "a + b + c", чтобы найти обратное число выражению, необходимо найти такое число x, при котором x + (a + b + c) = 0. Для этого можно использовать противоположные значения a, b и c и сложить их все вместе с противоположным знаком.
Третий метод, который стоит упомянуть, - метод обратного возведения в степень. Он предназначен для нахождения числа, которое возведенное в степень даст единицу. Например, если имеется выражение "a^b", чтобы найти обратное число выражению, необходимо найти такое число x, при котором x^b = 1. Это можно сделать с помощью извлечения корня с показателем 1/b из единицы.
В данном разделе мы рассмотрели лишь несколько основных методов нахождения числа с обратным значением выражения. Однако, существует и множество других подходов и алгоритмов, которые могут использоваться в зависимости от конкретной задачи. Важно понимать основные принципы и методы, чтобы быть готовыми к решению разнообразных математических задач.
Применение дроби: эффективные подходы и методы

В данном разделе мы рассмотрим различные стратегии и методы применения дробных чисел для достижения конкретных результатов. Используя разнообразные подходы, мы сможем сделать обратное значение выражения более точным и эффективным. Это позволит нам получить более точную информацию и улучшить качество решаемой задачи.
1. Выбор оптимальной точности В первую очередь, для получения наиболее точного обратного значения выражения, необходимо правильно выбирать точность дроби. От выбора точности будет зависеть точность результата. В этом разделе мы рассмотрим несколько методов определения оптимальной точности и способы ее применения. | 2. Аппроксимация выражения с использованием дробей Дроби могут быть эффективным инструментом для аппроксимации сложных выражений. При помощи дробей можно приблизить их значение и упростить дальнейшие вычисления. В этом разделе мы ознакомимся с основными методами аппроксимации и покажем примеры их применения. |
3. Использование десятичных дробей для точного результата Десятичные дроби представляют собой удобный и понятный способ представления чисел. В данном разделе мы рассмотрим применение десятичных дробей для получения наиболее точных обратных значений выражений. Такой подход позволяет получить результат с необходимой точностью и удобством использования. | 4. Применение непрерывных дробей для точных вычислений Непрерывные дроби представляют собой особый вид дробей, который может быть использован для более точных и эффективных вычислений обратных значений выражений. В данном разделе мы рассмотрим способы применения непрерывных дробей и их особенности. |
Умножение на инверсию числа: эффективные методы решения

В данном разделе мы рассмотрим эффективные приемы и техники для умножения на обратное число. Для достижения оптимальных результатов в математических вычислениях важно уметь находить обратную величину и использовать ее для умножения. В этом разделе мы рассмотрим несколько способов нахождения инверсии числа, которые помогут значительно упростить вычисления и повысить их точность.
- Метод десятичного деления: одним из наиболее популярных и простых способов нахождения инверсии числа является использование метода десятичного деления. Суть метода заключается в последовательном делении единицы на исходное число и приеме десятичного остатка. Этот метод позволяет найти инверсию числа с высокой точностью и минимальным количеством вычислений.
- Метод повторного приближения: данный метод основан на последовательном приближении к инверсии числа. Для этого используется начальное приближение, которое постепенно уточняется путем итераций. Этот метод позволяет получить более точный результат, особенно при работе с дробными числами.
- Метод использования разложения в сумму: данный метод основан на использовании разложения числа в сумму его десятичных разрядов. Путем соответствующего преобразования исходного числа, можно получить его инверсию. Этот метод особенно полезен при работе с числами, имеющими большое количество дробных разрядов.
Определение инверсии числа и умение находить ее является неотъемлемым навыком для успешного выполнения математических операций. При использовании эффективных методов умножения на обратное число, можно значительно сократить время вычислений и получить более точные результаты. Используйте представленные выше методы для повышения эффективности и точности ваших математических расчетов.
Применение дополнительного выражения до полной единицы

В данном разделе мы рассмотрим уникальный подход к нахождению числа, которое дополняет исходное значение до полной единицы. Основываясь на концепции дополнительного выражения до 1, мы исследуем возможные способы использования этой техники.
Мы обратим внимание на различные методы, которые позволяют получить число, являющееся дополнением исходного значения, таким образом, чтобы сумма между ними составляла полную единицу. Рассмотрим различные алгоритмы и подходы, позволяющие достичь этой цели.
Будем искать способы достижения дополнительного выражения до единицы с использованием различных операций и математических преобразований. Разберем методы, применяемые в различных областях, таких как финансы, информатика и математика. Отдельное внимание будет уделено эффективности и точности каждого из представленных методов.
При изучении данной темы мы рассмотрим практическое применение дополнительного выражения до 1 в различных сферах деятельности. Узнаем о его использовании при решении задач бухгалтерии, приближенных вычислений, а также в других практических ситуациях.
Расчет с использованием естественного логарифма

Естественный логарифм - это логарифм, который имеет основание, равное числу Эйлера (e). Он обычно обозначается как ln(x), где x - положительное число. Использование натурального логарифма позволяет решать различные задачи, связанные с обратным отображением чисел.
- Использование натурального логарифма в расчетах позволяет находить обратные значения функций, таких как экспоненциальные и степенные.
- Естественный логарифм также полезен при решении задач, связанных с процентами и ростом, так как он позволяет оценить необходимые изменения для достижения желаемого результата.
- Чтобы найти число, обратное значению выражения, можно использовать формулу обратного преобразования. Для этого нужно применить экспоненциальную функцию к натуральному логарифму исходного значения, что позволит получить обратное число.
Использование натурального логарифма - это один из простых, но эффективных способов решения математических задач и нахождения обратных значений. Он открывает новые возможности для точной и быстрой оценки чисел и служит незаменимым инструментом в различных областях науки, техники и финансов.
Применение матричных операций
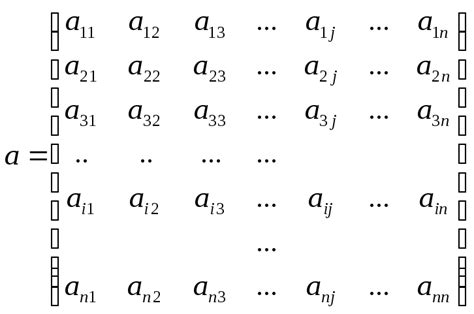
Одним из важных применений матричных операций является анализ данных. С помощью умножения матриц можно найти зависимости и взаимосвязи между различными переменными. Это особенно полезно в области машинного обучения, где матрицы используются для создания моделей и предсказаний.
Кроме того, матричные операции применяются для решения систем линейных уравнений. Умножение матриц и нахождение их обратной матрицы позволяют эффективно решать большие системы уравнений с множеством неизвестных переменных.
Еще одним применением матричных операций является обработка изображений. Матрицы используются для представления пикселей изображения, и их умножение или сложение позволяет применять различные фильтры и эффекты к изображению.
Важно отметить, что для успешного применения матричных операций необходимо иметь хорошие знания линейной алгебры. Умение составлять и умножать матрицы, находить их обратные и транспонированные матрицы является неотъемлемой частью работы с матричными операциями.
Применение программных инструментов для расчетов

В данном разделе рассмотрим важность использования различных программных средств для облегчения и ускорения вычислительных процессов. Благодаря профессиональным программам и инструментам, ученые, инженеры и специалисты в разных областях могут эффективно выполнять сложные математические операции, анализировать данные и находить оптимальные решения.
Технический прогресс сегодня позволяет использовать специализированные программные пакеты, такие как математические пакеты, численные методы и средства для символьных вычислений. При помощи таких инструментов возможно проводить сложные вычисления, решать уравнения, находить численные значения интегралов и дифференциальных уравнений, а также анализировать статистические данные.
К преимуществам использования программных средств для вычислений можно отнести ускорение процессов, снижение вероятности ошибок, автоматизацию рутинных операций, а также более удобный визуальный интерфейс для работы с данными. Важно отметить, что такие программные инструменты обладают гибкими возможностями настройки и позволяют адаптировать их под конкретные нужды пользователя.
| Программные средства | Области применения |
|---|---|
| Matlab | Инженерия, наука, физика |
| Mathematica | Символьные вычисления, математический анализ |
| Python с библиотекой NumPy | Научные исследования, анализ данных |
Различные программные инструменты предоставляют разнообразные функции и возможности для вычислений, поэтому важно подходить к выбору с учетом конкретных задач и требований. Правильное использование программных средств позволит улучшить эффективность работы и получить более точные и надежные результаты.
Практические примеры и упражнения для закрепления навыков

В данном разделе мы представим ряд практических примеров и упражнений, которые помогут закрепить ваши навыки в нахождении числа, обратного заданному значению выражения. Эти задачи позволят вам применить полученные знания на практике и улучшить вашу математическую грамотность.
Ниже приведена таблица с примерами задач, каждая из которых содержит описание выражения и требует нахождения числа, обратного его значению. Выполняя эти задачи, вы сможете лучше разобраться в техниках и методах решения, а также научитесь применять их в различных ситуациях.
| Пример задачи | Решение |
|---|---|
| Найдите число, обратное сумме двух третей данного числа. | Для нахождения обратного числа сумме, нужно разделить единицу на сумму. Таким образом, для данной задачи необходимо разделить единицу на сумму двух третей числа. |
| Определите число, обратное произведению половины числа и его квадрата. | Чтобы найти число, обратное данному выражению, нужно разделить единицу на произведение половины числа и его квадрата. |
| Найти обратное значение выражения: разность двух третей числа и его половины. | Для нахождения обратного значения данного выражения, нужно разделить единицу на его разность: две трети числа минус его половина. |
Решая данные примеры и выполняя упражнения, вы сможете совершенствовать свои навыки в нахождении обратного числа значения выражения. Не стесняйтесь пробовать различные подходы и методы решения, так как это поможет вам лучше понять математические концепции и развить аналитическое мышление.
Вопрос-ответ

Как найти число, обратное значению выражения?
Для того чтобы найти число, обратное значению выражения, нужно сначала вычислить значение этого выражения, затем взять его обратное значение. Например, если выражение равно 10, то число, обратное ему, будет равно 1/10 или 0.1.
Какая формула используется для нахождения числа, обратного значению выражения?
Формула для нахождения числа, обратного значению выражения, зависит от самого выражения. Например, если выражение имеет вид a/b, где a и b - числа, то число, обратное этому выражению, будет равно b/a.
Как найти число, обратное значению процента?
Для нахождения числа, обратного значению процента, нужно сначала вычислить значение процента, затем взять его обратное значение. Например, если процент равен 20%, то число, обратное ему, будет равно 1/20 или 0.05.
Какие есть способы быстро находить число, обратное значению выражения?
Существуют различные способы быстро находить число, обратное значению выражения. Один из них - использование калькулятора, который имеет функцию обратного значения. Другой способ - использование математических формул и свойств чисел для упрощения вычислений.
Можно ли найти число, обратное значению выражения без использования калькулятора?
Да, возможно найти число, обратное значению выражения без использования калькулятора. Для этого необходимо использовать математические свойства чисел, такие как обратные значения, десятичные дроби и др. Например, для нахождения числа, обратного значению 5, можно использовать дробь 1/5.
Что такое число обратное значению выражения?
Число обратное значению выражения - это число, при умножении на которое выражение равно единице.



