Путь разработчика всегда пролегает сквозь густой лес замысловатых задач, требующих истинного мастерства и креативности. В мире программирования Python является языком, который позволяет воплотить самые сложные идеи в жизнь. Но как быть, когда на пути возникают задачи, которые кажутся неразгаданными головоломками? Как найти правильное решение, чтобы ваш код стал примером идеальной логики и эффективности?
Цель данной статьи – помочь вам освоить искусство разгадывания задач по программированию на Python. Здесь вы найдете интересные и нестандартные примеры, сопровожденные подробными объяснениями. Мы покажем вам, как использовать синонимы кода, чтобы достичь удивительных результатов и создать программы, которые будут восхищать своей элегантностью и функциональностью.
Необходимые знания и навыки в программировании – это только первый шаг. Разгадывание задач требует готовности к постоянному развитию и самостоятельной исследовательской работы. Мы предлагаем вам инструменты и методы, которые помогут вам освоить эти навыки, пошагово и открытиями восстанавливая картину, которую рисует вам каждая задача. Готовы погрузиться в мир разгадывания головоломок программирования на Python?
Обработка задач программирования на языке Python: наглядные и полезные примеры

В этом разделе мы воспользуемся различными синонимами и альтернативными выражениями, чтобы подробно рассмотреть основные принципы решения задач программирования на языке Python. Мы рассмотрим примеры программ и пошагово объясним, как они работают и как достичь желаемого результата. Вам не нужно будет самостоятельно или много раз нажимать по кнопкам - мы предоставим конкретные примеры, чтобы вы могли ясно представить себе каждый шаг решения задачи.
В каждом примере вы найдете разнообразные алгоритмы и способы решения задач на языке Python. Это поможет вам не только получить глубокое понимание синтаксиса языка и его конструкций, но и научиться применять их в реальных ситуациях. Мы также рассмотрим использование различных структур данных, операций и методов, которые могут быть полезны при работе над задачами программирования.
Анализ простой задачи на расчет факториала числа
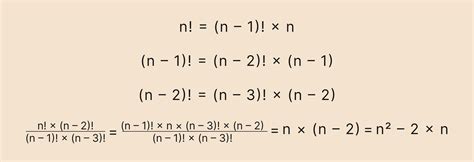
В данном разделе мы рассмотрим подробный анализ простой задачи, связанной с вычислением факториала числа. Мы будем изучать способы решения этой задачи без использования конкретных определений и фокусироваться на общей идее и подходах к решению.
Для начала мы рассмотрим математическую основу задачи, изучив понятие факториала и его свойства. Затем мы покажем различные способы реализации алгоритма расчета факториала числа на языке Python. Мы рассмотрим как рекурсивный, так и итеративный подходы и проведем сравнение их эффективности.
Для лучшего понимания алгоритмов, мы представим их пошаговое описание и приведем примеры кода. Также мы обсудим различные варианты оптимизации алгоритмов, учитывая особенности вычисления факториала числа.
В целях наглядности, мы также представим таблицу, где будут указаны временные характеристики каждого решения и их сравнение в зависимости от размера входных данных. Это поможет читателю лучше понять различия между реализациями и выбрать оптимальный подход к решению задачи.
| Алгоритм | Время выполнения | Ограничения |
|---|---|---|
| Рекурсивный | ... | ... |
| Итеративный | ... | ... |
Как найти наибольший общий делитель (НОД) двух чисел?

Существуют различные алгоритмы для нахождения НОД, но одним из самых известных и простых является алгоритм Евклида. Он основан на следующей идее: если НОД чисел a и b равен c, то НОД чисел a и b также равен НОД чисел b и a - b.
Алгоритм Евклида можно применить следующим образом:
- Возьмите два заданных числа, для которых нужно найти НОД.
- Если одно из чисел равно нулю, то НОД равен другому числу.
- Вычтите из большего числа меньшее число.
- Повторите шаги 2 и 3 с новыми числами до тех пор, пока одно из чисел не станет равным нулю.
- Оставшееся число является НОД заданных чисел.
Применим алгоритм Евклида на примере поиска НОД чисел 24 и 18:
- Числа 24 и 18 не равны нулю.
- 24 - 18 = 6.
- Числа 18 и 6 не равны нулю.
- 18 - 6 = 12.
- Числа 12 и 6 не равны нулю.
- 12 - 6 = 6.
- Числа 6 и 6 не равны нулю.
- 6 - 6 = 0.
- НОД чисел 24 и 18 равен 6.
Алгоритм Евклида является эффективным способом нахождения НОД двух чисел, и его можно использовать в различных программных средах, включая Python. Решение задач по поиску НОД позволяет обеспечить оптимальные вычисления и эффективное использование ресурсов в программе.
Используя алгоритм Евклида, вы можете легко решать задачи, связанные с поиском НОД двух чисел в программировании.
Метод пузырька: эффективный способ сортировки массива
Вы, наверное, не раз сталкивались с ситуацией, когда необходимо упорядочить элементы массива. В данном разделе мы рассмотрим практическое применение метода пузырька для решения данной задачи. Данный метод достаточно прост и понятен, что делает его широко используемым во многих приложениях.
Идея метода пузырька состоит в постепенном "всплытии" наибольших элементов массива до их окончательной позиции.
Основная идея метода заключается в сравнении каждого элемента с его соседними и, при необходимости, их обмене местами. Таким образом, самый большой элемент "всплывает" на последнюю позицию массива. Этот процесс повторяется, пока все элементы не будут расположены в нужном порядке.
Преимущество данного метода состоит в его простоте и понятности. Он хорошо подходит для небольших массивов и в случае, когда требуется выполнить сортировку в кратчайшие сроки. Однако, следует учитывать, что метод пузырька не является самым эффективным алгоритмом для сортировки больших массивов.
В данном разделе мы рассмотрели практическое использование метода пузырька для сортировки массива. Вы можете использовать этот метод в своих проектах, если требуется базовая сортировка небольших массивов.
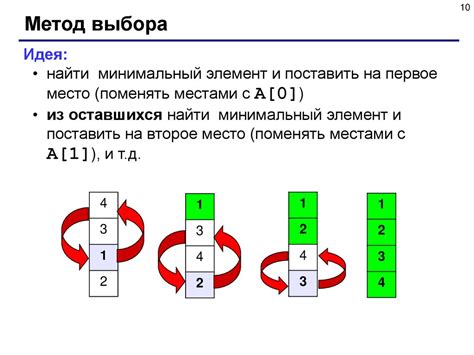
Алгоритм поиска наименьшего элемента в списке

В данном разделе объясним алгоритм поиска наименьшего элемента в заданном списке. Мы рассмотрим простой и эффективный подход, который позволяет найти минимальный элемент без лишних итераций по списку.
| Шаг | Описание |
|---|---|
| 1 | Присвоить переменной "минимальный_элемент" первый элемент списка. |
| 2 | Пройти по оставшимся элементам списка, начиная со второго элемента. |
| 3 | Сравнить текущий элемент с переменной "минимальный_элемент". Если текущий элемент меньше "минимального_элемента", обновить значение "минимального_элемента". |
| 4 | Повторять шаги 2-3 для всех оставшихся элементов списка. |
| 5 | По завершении цикла поиска наименьшего элемента, переменная "минимальный_элемент" будет содержать значение самого маленького элемента списка. |
На данный момент мы рассмотрели алгоритм поиска наименьшего элемента в списке. Далее приведем пример кода на языке Python, который демонстрирует применение этого алгоритма.
Использование рекурсии для вычисления факториала: основная концепция

Факториал числа - это результат произведения всех положительных целых чисел от 1 до данного числа. Будучи математической операцией, вычисление факториала также может быть реализовано с использованием программирования. Для решения этой задачи мы можем использовать метод рекурсии.
Рекурсивная функция для вычисления факториала - это функция, которая вызывает саму себя с некоторыми изменениями аргументов, пока не будет достигнуто базовое условие. В нашем случае, базовое условие - это факториал числа 0 или 1, который равен 1.
Анализ сложной задачи по подсчету суммы чисел Фибоначчи
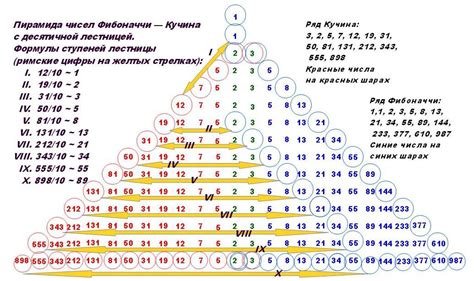
В данном разделе мы рассмотрим сложную задачу, связанную с вычислением суммы чисел Фибоначчи. Числа Фибоначчи представляют собой последовательность чисел, в которой каждое число равно сумме двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8 и так далее. Наша задача состоит в вычислении суммы определенного количества чисел Фибоначчи.
Для решения этой задачи нам потребуется использовать различные алгоритмы и структуры данных, такие как циклы, рекурсия и массивы. Мы рассмотрим каждый из этих подходов и поэтапно разберем, как они помогают в решении данной задачи.
- И, наконец, третий подход - использование массива. Мы создадим массив, в котором будем хранить все числа Фибоначчи до требуемого номера. Затем мы пройдем по этому массиву и вычислим сумму чисел, после чего выведем результат.
Таким образом, в данном разделе мы рассмотрели различные подходы к решению задачи вычисления суммы чисел Фибоначчи. Каждый из этих подходов имеет свои преимущества и может быть использован в зависимости от конкретных требований и условий задачи.
Нахождение всех простых чисел до заданного числа

Этот раздел посвящен решению задачи, связанной с поиском всех простых чисел, которые меньше или равны определенному числу. Мы представим пример алгоритма решения данной задачи и дадим подробное объяснение каждого шага.
Для начала, рассмотрим, что такое простое число. Простым числом называется натуральное число, большее единицы, которое имеет только два делителя: 1 и само число. Например, числа 2, 3, 5, 7 являются простыми, так как они не имеют других делителей, кроме 1 и себя.
Подход к решению задачи будет основан на использовании алгоритма "Решето Эратосфена". Этот алгоритм позволяет найти все простые числа до заданного числа путем отсеивания составных чисел.
Для начала, создадим таблицу с числами от 2 до заданного числа. Начнем с первого числа и будем последовательно отсеивать все его кратные числа (кроме самого числа), помечая их как составные. После этого перейдем к следующему непомеченному числу и выполним ту же операцию. Процесс будет продолжаться до тех пор, пока не будут перебраны все числа.
| Число | Пометка |
| 2 | Простое |
| 3 | Простое |
| 4 | Составное |
| 5 | Простое |
| 6 | Составное |
| 7 | Простое |
| 8 | Составное |
| 9 | Составное |
| 10 | Составное |
В результате работы алгоритма, все помеченные числа будут являться составными, а непомеченные - простыми. Таким образом, мы сможем получить все простые числа до заданного числа.
Реализация данного алгоритма на языке Python позволяет легко использовать его для нахождения простых чисел в заданном диапазоне. Будучи одним из самых эффективных способов нахождения простых чисел, алгоритм "Решето Эратосфена" является популярным и широко используется в программировании.
Методика объяснения решения задачи на проверку наличия элемента в списке

В этом разделе мы рассмотрим подходы и принципы, которые помогут вам эффективно решать задачи, связанные с проверкой наличия элемента в списке. Мы представим вам несколько методов, которые помогут вам справиться с такой задачей.
Во-первых, вам необходимо правильно сформулировать цель задачи и понять, что именно нужно проверить в списке. Вы должны четко представлять, какой тип данных вы ожидаете получить в результате проверки наличия элемента в списке.
Во-вторых, вы можете воспользоваться циклом, чтобы перебрать все элементы списка и проверить, содержит ли он искомый элемент. Вы можете использовать условные операторы, чтобы определить, какая реакция должна быть в случае нахождения или отсутствия элемента.
Кроме того, вы можете использовать встроенные функции, такие как in, чтобы упростить процесс проверки наличия элемента в списке. Эта функция вернет True, если элемент присутствует в списке, и False, если элемент отсутствует. Вы можете использовать эту функцию в условных операторах, чтобы определить, какая реакция должна быть в каждом случае.
Анализ задачи: поиск наибольшей последовательности нулей в двоичном числе
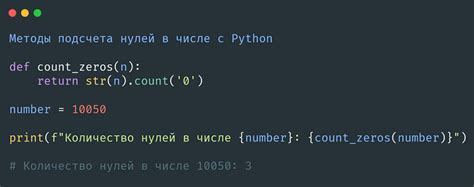
В данном разделе мы рассмотрим способы решения интересной задачи, связанной с поиском максимальной подпоследовательности нулей в бинарном числе. Мы изучим различные подходы, объясним их основные идеи и покажем примеры кода на языке Python.
Задача заключается в нахождении наибольшей последовательности нулей, которая может встретиться в двоичном числе. Для этого нам нужно разработать алгоритм, который способен обрабатывать входное число и находить самую длинную последовательность нулей.
Мы рассмотрим различные подходы к решению этой задачи.
Первый подход будет основан на простом методе перебора, при котором мы последовательно проходим по каждой цифре в двоичном числе и ищем самую длинную последовательность нулей. Этот метод является наивным, но позволяет нам лучше понять суть задачи и ознакомиться с основными концепциями решения.
| Метод | Описание | Пример кода |
|---|---|---|
| Перебор | Метод последовательного перебора цифр числа с поиском наибольшей последовательности нулей. | ```python def find_longest_zero_sequence(num): # реализация алгоритма pass ``` |
Также мы рассмотрим более оптимальные подходы, использующие принципы динамического программирования. Они позволяют существенно ускорить процесс поиска и улучшить производительность программы.
Как определить, является ли число палиндромом

Для решения задачи проверки числа на палиндромность существует несколько подходов. Один из них - это превратить число в строку и сравнить его с перевернутой версией этой строки. Если значения совпадают, то число является палиндромом, в противном случае - нет.
Для превращения числа в строку мы можем воспользоваться функцией str(), которая преобразует число в строковый тип данных. Затем, для получения перевернутой строки, можно воспользоваться срезами, указывающими шаг -1, что означает проход по строке в обратном порядке. После этого само число и его перевернутая версия сравниваются на равенство.
Другой подход заключается в использовании арифметических операций для выделения цифр числа и их последующего сравнения. Например, число 121 можно разделить на цифры 1, 2 и 1, и их положение в числе симметрично. Если же число не имеет положения цифр в числе, оно не является палиндромом.
- Преобразуйте число в строку, переверните его и сравните с исходным числом.
- Используйте арифметические операции для выделения цифр числа и их последующего сравнения.
Теперь, у вас есть два способа проверки числа на палиндромность. Вы можете выбрать подходящий вариант для своей задачи и приступить к решению!
Вопрос-ответ

Какие примеры программ на Python можно использовать для решения задач по программированию?
Примерами программ на Python для решения задач по программированию могут быть такие задачи как вычисление среднего значения элементов массива, сортировка списка чисел, поиск наибольшего числа в списке и многие другие. Все зависит от конкретной задачи, которую необходимо решить.
Какие методы и функции в Python могут быть полезны при решении задач по программированию?
В Python существует множество полезных методов и функций, которые могут быть использованы при решении задач по программированию. Например, методы сортировки списка, функции для работы с числами, встроенные функции для работы со строками и многое другое. Важно выбрать подходящие методы и функции в зависимости от поставленной задачи.
Можно ли использовать Python для решения сложных задач по программированию?
Да, Python можно использовать для решения сложных задач по программированию. Python является мощным и гибким языком программирования, который предлагает множество инструментов и библиотек для работы с различными типами данных и алгоритмами. С помощью Python можно решать задачи как средней сложности, так и очень сложные задачи.
Какие преимущества есть у использования Python для решения задач по программированию?
Есть несколько преимуществ использования Python для решения задач по программированию. Во-первых, Python имеет простой и понятный синтаксис, что делает его доступным для новичков в программировании. Во-вторых, Python обладает множеством встроенных функций и библиотек, которые позволяют решать задачи эффективно и быстро. Также Python поддерживает объектно-ориентированное программирование, что позволяет создавать модульные и поддерживаемые программы.