В этой статье мы хотим рассказать о необычном и интересном способе изучения геометрических фигур. Уже знакомые нам понятия "диагонали", "трапеции", "углы" и "анализ" на этот раз займут побочные роли, чтобы уступить место новой концепции - деление углов пополам.
Представьте себе, что каждая фигура - это небольшой пазл, состоящий из абстрактных частей. Наша задача - проанализировать их форму, изучить связь между углами и применить технику деления углов пополам для получения уникальной информации о каждой фигуре. Необычный, не правда ли?
Особенности диагонали в фигуре с противоположными параллельными сторонами

Существует стройная связь между определенными линиями, которые охватывают фигуру с противоположными боковыми сторонами и соприкасаются с ее вершинами. Эта связь обусловлена величиной и направлением диагонали, разрезающей фигуру на два треугольника. Понимание и владение этой концепцией имеет значительное значение при изучении и анализе геометрических схем и структур.
В данном разделе мы рассмотрим особенности работы с линией, которая соединяет противоположные вершины фигуры, содержащей прямые стороны. Такая линия называется диагональю.
Диагональ - это сегмент, соединяющий вершины фигуры и проходящий внутри нее. Она имеет способность находить середину каждого из углов в фигуре, что является ее особенностью. Направление диагонали и особенности ее влияния на угловые отношения фигуры могут иметь значительное влияние на ее геометрические свойства и аналитические решения.
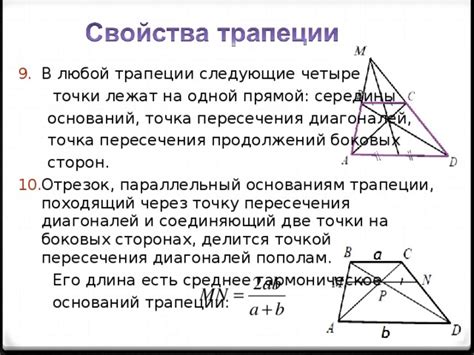
Диагонали играют важную роль в анализе фигур и структур, таких как трапеции, и могут быть использованы для определения свойств, например, параллельности сторон, различных углов фигуры и других характеристик.
Свойства и особенности геометрического характера диагонали в четырехугольнике с параллельными сторонами

- Уникальные угловые свойства: изучение связи ангулярной геометрии диагонали с остальными углами трапеции, выявление паттернов и закономерностей, связанных с расположением диагонали относительно остальных элементов конструкции.
- Взаимосвязь диагонали и длины сторон: анализ взаимосвязи длины диагонали и длин смежных сторон трапеции, определение условий, при которых изменение длины диагонали влияет на структуру и форму трапеции.
- Симметрия и смежные свойства: рассмотрение симметричных отношений диагоналей в трапеции, сравнение их длин и угловых свойств, выделение смежных свойств, связывающих диагонали
Нахождение размера пространственной диагонали в четырехугольнике со смещением углов
В этом разделе рассмотрим метод определения длины пространственной диагонали в фигуре, которая имеет четыре стороны, причем две из них параллельны. Применив определенные геометрические преобразования, мы сможем вычислить данную характеристику, не прибегая к измерению отрезков или специальным инструментам.
Проявив аналитический подход, мы сможем определить длину диагонали в трапеции, используя основные характеристики фигуры, такие как длина ее оснований и углы. В терминах математических операций, мы рассмотрим метод, основанный на делении углов трапеции пополам, что позволит нам представить данную диагональ в виде линии, соединяющей две пары параллельных сторон.
Для нахождения этой величины мы воспользуемся синусами и косинусами треугольников, образованных диагональю и сторонами трапеции. Благодаря этому подходу, мы сможем установить связь между углами и длиной диагонали, открывая новые возможности для вычисления этой величины без необходимости проведения специальных измерений.
Таким образом, на примерах и разборе расчетов мы изучим процесс нахождения размера диагонали в трапеции и усвоим метод, основанный на делении углов пополам. Это поможет нам более глубоко понять геометрические связи и способы определения характеристик фигур, что может быть полезно в решении различных задач из области геометрии и пространственной аналитики.
Зависимость длины противоположной стороны от углов трапеции
Длина противоположной стороны трапеции имеет прямую зависимость от мер углов, характеризующих фигуру. Чем больше углы трапеции, тем длиннее становится противоположная диагональ.
Важно отметить, что углы трапеции делятся на две пары, каждая из которых имеет свою роль в определении длины противоположной стороны. Углы, расположенные у основания трапеции, определяют наклон противоположной стороны и влияют на ее длину. С другой стороны, углы, расположенные у основания и сторонах трапеции, влияют на угол между противоположной стороной и основанием.
Исследования показали, что при равных абсолютных значениях углов трапеции пропорция между длиной противоположной стороны и углами неизменна. Однако, при изменении одного угла и сохранении остальных пропорция может измениться, внося корректировки в длину противоположной диагонали.
- Увеличение угла у основания трапеции приводит к укорочению длины противоположной стороны и уменьшению угла между диагональю и основанием.
- Увеличение угла у основания и угла между диагональю и основание влечет удлинение противоположной стороны и увеличение величины угла между диагональю и основанием.
- Изменение углов у сторон трапеции влияет на угол между диагональю и основанием, что также отражается в изменении длины противоположной стороны.
Таким образом, длина противоположной диагонали в трапеции является функцией углов, причем изменение одного угла может оказывать неоднозначное влияние на ее длину в сочетании с остальными мерами углов.
Исследование возможностей использования диагоналей в трапеции для решения геометрических задач
Этот раздел посвящен применению диагоналей в трапеции для эффективного решения различных геометрических задач. Мы рассмотрим несколько интересных примеров, где использование диагоналей помогает нам найти нужные параметры фигур и объясним применение данного метода на практике.
В первом примере мы исследуем задачу о нахождении площади трапеции, когда известны только ее диагонали и угол между ними. Мы рассмотрим конкретный пример и подробно объясним шаги, необходимые для решения задачи с использованием диагоналей.
Далее, мы рассмотрим задачу о нахождении длин боковых сторон трапеции, когда известны только ее диагонали и угол между ними. Мы представим конкретный пример и обсудим методику поиска данных параметров, основываясь на свойствах диагоналей и используя геометрические выкладки.
Влияние диагонали на равномерность углов в четырехугольниках
Изучение влияния диагонали на равномерное разделение углов можно провести через анализ нескольких примеров. Представим себе, что четырехугольник - это парк, а его углы представляют собой скамейки, на которых сидят посетители. Если диагональ проходит через центр парка, то она распределяет посетителей равномерно, создавая приятную атмосферу и ощущение гармонии. Однако, если диагональ не проходит через центр парка, то сидящие на скамейках посетители могут создавать впечатление неравномерности и напряжения.
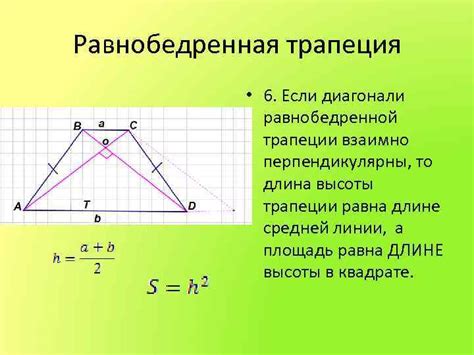
- При рассмотрении равнобокой трапеции диагональ равномерно делит два угла, образуя их равные части. Это свойство способствует симметричности и гармонии в геометрической структуре фигуры.
- Для прямоугольной трапеции диагональ равномерно делит на две части прямой и обратный углы, сохраняя при этом основное свойство прямого угла.
- Углы в произвольной трапеции разделяются диагональю в неравных пропорциях, что создает ощущение непарности и динамичности в геометрической структуре фигуры.
Таким образом, диагональ влияет на разделение углов в трапеции пополам, но это свойство проявляется различным образом в зависимости от типа трапеции и ее геометрической структуры. Такое понимание поможет нам более глубоко изучить свойства и особенности трапеций.
Интересные факты и возможности диагонали в четырехугольнике с параллельными сторонами
В математике существует множество фактов и приложений, связанных с диагональю в четырехугольнике, у которого есть параллельные стороны. Эта линия, пересекающая несколько углов и сторон, выполняет не только важную геометрическую функцию, но и имеет практическое применение в различных областях.
Одно из интересных свойств диагонали в таком четырехугольнике - ее способность разбивать фигуру на два равных треугольника. Подобное разделение позволяет проводить различные вычисления и рассматривать геометрические особенности каждого треугольника отдельно.
Важно отметить, что диагональ также может играть роль опорной оси для равномерного размещения объектов внутри четырехугольника. Это особенно полезно в архитектуре и строительстве, где нужно рационально расположить элементы внутри пространства и учесть геометрические пропорции.
С приложением диагонали в четырехугольнике с параллельными сторонами связана и геометрическая концепция сегмента относительно этой линии. С помощью сегментов можно, например, рассчитать площади различных частей фигуры и проводить дальнейшие геометрические исследования.
Интересно отметить, что диагональ в четырехугольнике может служить наглядным примером применения теоремы Пифагора или других геометрических закономерностей. Такие примеры могут быть полезны для обучения и визуализации математических концепций.
Вопрос-ответ
Зачем диагональ в трапеции делит углы пополам?
Деление углов трапеции пополам диагональю позволяет получить два равных угла, что упрощает решение задач и нахождение различных значений этой фигуры.
Какая формула используется для нахождения длины диагонали в трапеции?
Для нахождения длины диагонали в трапеции используется теорема косинусов, где диагональ является стороной, а другие стороны – это основания трапеции и боковые стороны.
Можно ли использовать деление углов пополам диагональю для других четырехугольников?
Да, деление углов пополам диагональю может применяться не только для трапеции, но и для других четырехугольников, таких как ромб, параллелограмм и прямоугольник. Это свойство позволяет найти значения угловых и линейных величин в этих фигурах.