Взглянув на треугольник abc, вопрос о его основных характеристиках возникает непременно. И одним из ключевых показателей, который на первый взгляд может показаться незначительным, является его гипотенуза – главный элемент, определяющий пропорции и устойчивость всего треугольника.
Можно провести аналогию между гипотенузой треугольника и его "костяком". Прочный и равномерный по всей длине, этот элемент обеспечивает основу для всех других линий и углов треугольника. Его длина имеет непосредственное влияние на его структуру и геометрию. А именно – величина этой гипотенузы может определять самую суть треугольника и его форму.
Долгое время было известно, что длина гипотенузы внутри треугольника abc равна корню из 2 см. Это значительное измерение подразумевает, что каждый из его элементов, каждая сторона, каждый угол пропорционально связаны и гармонично соответствуют друг другу. Однако, этот фундаментальный показатель является скрытым гранитом мира треугольников, который необходимо раскрыть научным путем, чтобы полностью понять геометрию и свойства этой фигуры.
Определение основной стороны треугольника и ее взаимосвязь с остальными сторонами

В данном разделе будет рассмотрена основная сторона треугольника, которая имеет особое значение и связана с другими сторонами этой геометрической фигуры. Мы осветим важность определения и вычисления этой стороны и разберем, как она взаимодействует с остальными элементами треугольника.
Основная сторона представляет собой наибольшую сторону треугольника, которая является главной мерой его размера. Важно отметить, что в каждом треугольнике есть только одна основная сторона. Эта сторона соединяет две вершины треугольника и имеет особую роль в геометрических вычислениях и свойствах треугольника.
Одна из ключевых связей основной стороны с остальными сторонами треугольника - это ее взаимосвязь с гипотенузой. Гипотенуза, являющаяся самой длинной из сторон треугольника, имеет прямое отношение к основной стороне. Взаимосвязь этих сторон представляет собой одно из основных свойств прямоугольного треугольника и может быть выражена с помощью таких математических понятий, как теорема Пифагора и соотношения между сторонами треугольника.
Роль формулы Пифагора в вычислении длины гипотенузы треугольника abc

Формула Пифагора устанавливает зависимость между сторонами прямоугольного треугольника и позволяет вычислить длину гипотенузы, зная длины его катетов. В ее основе лежит понятие пифагоровых троек, состоящих из трех целочисленных значений, удовлетворяющих соотношению a^2 + b^2 = c^2, где a и b - длины катетов, а c - длина гипотенузы.
| Сторона треугольника | Синонимы |
| Гипотенуза | Диагональ, основная сторона, противоположная сторона |
| Треугольник | Триугольник, трехугольник, многоугольник с тремя сторонами |
| Длина | Размер, величина, протяженность |
| Корень из 2 см | Иррациональное значение длины, квадратный корень из двух см |
Используя формулу Пифагора, можно вычислить длину гипотенузы треугольника abc, если известны длины его катетов. Это позволяет не только находить пропущенные значения в геометрических задачах, но и применять принципы формулы в различных областях науки и техники.
Пример расчета длины гипотенузы треугольника с использованием формулы Пифагора
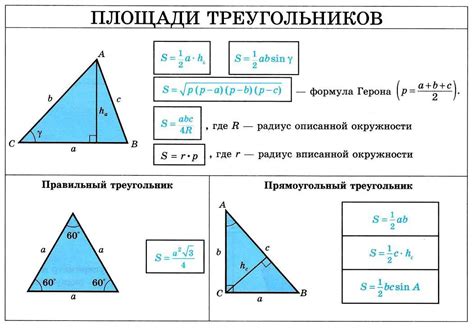
В данном разделе мы рассмотрим пример расчета длины одной из сторон треугольника, используя знаменитую формулу Пифагора. Формула Пифагора позволяет найти длину гипотенузы треугольника исходя из длин его катетов. Она основывается на геометрической теореме Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Представим ситуацию, в которой длина гипотенузы треугольника составляет корень из 2 сантиметра. Используя формулу Пифагора, мы можем определить длины катетов этого треугольника. Зафиксируем один из катетов и обозначим его длину как "а". Второй катет - "b". Таким образом, гипотенуза будет равна корню из 2, что можно записать в виде c = √2.
Воспользуемся формулой Пифагора: a^2 + b^2 = c^2. В нашем случае это a^2 + b^2 = (√2)^2. Раскрыв скобки, получим a^2 + b^2 = 2. Зная, что длина гипотенузы составляет корень из 2, мы можем записать гипотезу a^2 + b^2 = 2.
Исходя из данной гипотезы, мы можем рассчитать значения катетов треугольника. Например, предположим, что один из катетов равен 1 сантиметру. В таком случае, мы можем подставить полученные значения в формулу Пифагора и решить уравнение.
Это лишь один из множества примеров расчета длины гипотенузы треугольника с использованием формулы Пифагора. Эта формула является одной из основных и наиболее широко используемых в геометрии и математике. Она позволяет не только находить длину гипотенузы, но и проводить различные вычисления, связанные с прямоугольными треугольниками.
Задачи на вычисление длины гипотенузы треугольника abc при известных длинах других сторон
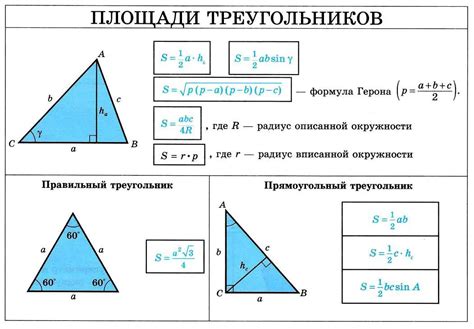
В данном разделе мы рассмотрим задачи, связанные с вычислением длины гипотенузы треугольника abc, когда известны длины его других сторон. Мы рассмотрим различные сценарии и способы решения этих задач, используя различные формулы и математические методы.
Длина гипотенузы является одним из основных параметров треугольника, а ее вычисление может быть ключевым шагом в решении множества геометрических задач. В данном разделе мы рассмотрим как вычислить длину гипотенузы треугольника abc, когда известны длины его других сторон. Мы рассмотрим несколько типов задач и предоставим подробное объяснение каждого случая.
| Тип задачи | Сценарий | Формулы и методы решения |
|---|---|---|
| Задача 1 | Известны длины двух катетов треугольника abc | Применение теоремы Пифагора |
| Задача 2 | Известна длина одного катета и гипотенузы треугольника abc | Применение теоремы Пифагора и пропорции треугольников |
| Задача 3 | Известны длины одного катета и угла между катетами треугольника abc | Применение тригонометрических функций |
Каждая задача имеет свою уникальную постановку и метод решения, поэтому в данном разделе мы предоставим подробные инструкции по решению каждой из них. Мы демонстрируем вычисления на конкретных примерах и объясняем каждый шаг, чтобы вы могли легко применить полученные знания и решить подобные задачи самостоятельно. Уверены, что после изучения данного раздела вы сможете успешно решать задачи на вычисление длины гипотенузы треугольника abc при известных длинах других сторон.
Определение длины гипотенузы треугольника abc через значение корня из 2 см
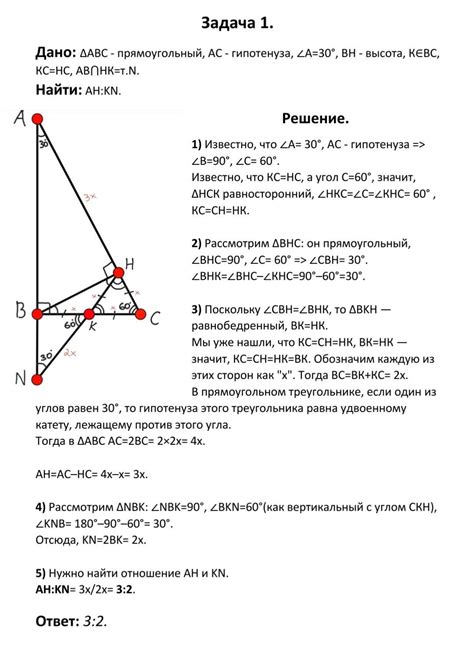
В данном разделе будет представлено доказательство того, что в треугольнике abc длина гипотенузы равна корню из 2 см. Будут использованы свойства треугольников и основные определения, чтобы объяснить эту связь.
Для начала, давайте рассмотрим определение гипотенузы: это сторона треугольника, которая противоположна прямому углу. В нашем случае, давайте обозначим эту сторону как c. Также у нас есть две другие стороны треугольника, обозначим их как a и b.
Используя теорему Пифагора, мы знаем, что квадрат длины гипотенузы равен сумме квадратов длин двух других сторон: c² = a² + b². В данном случае, мы хотим доказать, что c = √2 см.
Предположим, что длина сторон a и b также равна √2 см. Тогда квадраты длин a и b будут равны 2 см² каждый. Если мы сложим эти два значения, получим сумму квадратов сторон a и b, которая равна 4 см².
Теперь, применив теорему Пифагора, мы можем убедиться, что c² = a² + b² = 4 см². Извлекая квадратный корень из обеих сторон, мы получаем с = √4 см = 2 см. Поэтому, если длина сторон a и b равна корню из 2 см, то и длина гипотенузы c также равна корню из 2 см.
Таким образом, доказательство того, что длина гипотенузы треугольника abc равна корню из 2 см, основывается на применении теоремы Пифагора и свойств треугольников.
| Свойство | Описание |
|---|---|
| Теорема Пифагора | В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. |
| Гипотенуза | Сторона треугольника, противоположная прямому углу. |
Особенности треугольников с гипотенузой, равной корню из 2 см
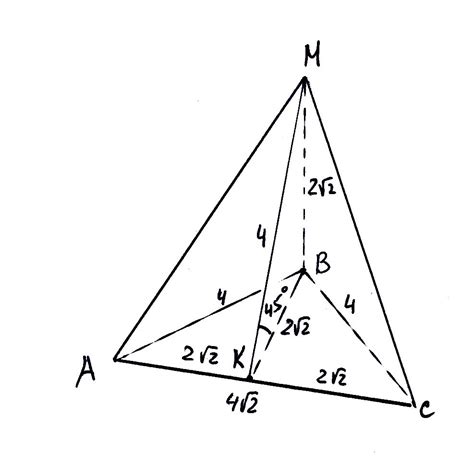
В данном разделе мы рассмотрим особенности треугольников, у которых самая длинная сторона, называемая гипотенузой, имеет длину, равную корню из 2 сантиметров. В таких треугольниках мы столкнемся с необычными свойствами и специфичными соотношениями между их сторонами и углами.
Существует несколько важных факторов, которые следует учитывать, при изучении такого типа треугольников. Во-первых, гипотенуза является наибольшей стороной треугольника и образует прямой угол с двумя другими сторонами. Это означает, что треугольник обладает свойствами прямоугольного треугольника. Во-вторых, длины и соотношения других двух сторон (катетов) будут зависеть от длины гипотенузы.
Одно из основных соотношений, присущих таким треугольникам, это теорема Пифагора. Она утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов: a^2 + b^2 = c^2, где a и b - катеты, а c - гипотенуза. Таким образом, при известной длине гипотенузы, мы можем определить длины катетов данного треугольника.
Благодаря таким свойствам, треугольники с гипотенузой, равной корню из 2 см, являются основой для решения множества задач и геометрических конструкций. Они также обладают интересными свойствами, связанными с углами и площадью треугольника, которые дополнительно могут быть исследованы и изучены.
Как определить длину гипотенузы треугольника без использования формулы Пифагора

В данном разделе мы рассмотрим метод, позволяющий вычислить длину гипотенузы треугольника с помощью альтернативных подходов, без использования формулы Пифагора. Вместо привычных определений и терминов, применим более нестандартные выражения для объяснения этой концепции.
Необычные подходы к расчету длины гипотенузы
Вместо традиционного подхода, использующего теорему Пифагора и корень из 2, мы предложим несколько альтернативных методов, позволяющих без лишних формул и сложных вычислений определить длину гипотенузы треугольника. Они основаны на простых логических рассуждениях и геометрических свойствах фигуры.
Метод "Геометрический фокус"
Этот метод основан на неожиданном свойстве треугольника, которое позволяет найти длину его гипотенузы, даже не зная все стороны и углы. Ключевой идеей является использование определенного соотношения между длинами сторон и углами треугольника, который помогает нам "разгадать" его гипотенузу без применения формулы Пифагора.
Метод "Ломаная линия"
В этом методе мы будем использовать идею ломаных линий и их связь с длинами сторон треугольника. С помощью графического представления мы сможем найти способ определения длины гипотенузы без использования формулы Пифагора.
Роль гипотенузы в прямоугольных треугольниках и их особенности
Особенность гипотенузы заключается в её длине и определении через другие стороны треугольника. Обозначается она буквой "с" или "Г" и представляет собой сторону, противоположную прямому углу. Отличительной чертой гипотенузы является то, что она всегда самая длинная сторона треугольника, и её длина может быть выражена с помощью теоремы Пифагора.
Гипотенуза обладает рядом интересных свойств, которые делают её важным элементом в решении различных геометрических задач:
- Гипотенуза является главной диагональю прямоугольного параллелепипеда и позволяет определить его объём.
- Она определяет высоту и медиану по отношению к гипотенузе в прямоугольном треугольнике.
- Гипотенуза обладает наибольшей длиной среди всех сторон, что влияет на соотношение других сторон и углов треугольника.
- По длине гипотенузы можно определить чувствительность пациента к определённым лекарственным препаратам.
Таким образом, гипотенуза играет важную роль в прямоугольных треугольниках и позволяет решать разнообразные задачи, связанные с геометрией, физикой, медициной и другими областями науки.
Значимость стороны треугольника в задачах с практическим применением

Существуют различные способы применения понятий длины гипотенузы в реальных задачах. Однако, возможности использования данной характеристики треугольника в практических ситуациях не ограничиваются только определенными терминами и именами. Геометрические пропорции и соотношения могут быть применены для измерения и описания различных объектов и явлений в областях таких как архитектура, инженерия и физика.
Косвенные приложения длины гипотенузы могут быть найдены в различных аспектах повседневной жизни. Например, в архитектуре данная характеристика может быть использована для расчета стабильности и прочности зданий, определения правильной конструкции ступеней на лестницах или определения размеров фундамента. В инженерных расчетах гипотенуза может быть использована для определения длины кабеля, необходимого для прокладки между двумя точками, или для оценки необходимой длины провода для электрического соединения. Кроме того, эта характеристика может быть применена при вычислении длины траектории движения объекта или определении дистанции между двумя точками на плоскости.
Учитывая существенную роль длины гипотенузы в реальных практических ситуациях, понимание и умение применять данную характеристику треугольника позволяет решать широкий спектр задач. Знание геометрических концепций и их приложений можно использовать для решения практических проблем, а также для более глубокого анализа и понимания окружающего мира.
Вопрос-ответ

Как найти длину гипотенузы треугольника, если известна его площадь?
Для нахождения длины гипотенузы треугольника, нам необходимо знать длины его сторон. Площадь треугольника равна половине произведения длин его катетов, и по формуле площади треугольника можно найти одну из сторон. Однако, только по площади треугольника без дополнительной информации нельзя однозначно определить длину его гипотенузы.
Можно ли рассчитать длину гипотенузы треугольника, если известна длина одного катета и угол между ними?
Да, длину гипотенузы треугольника можно рассчитать, если известна длина одного катета и угол между ними. Для этого можно воспользоваться формулой тригонометрии - косинуса. Если известны длина катета и угол между ними, то длину гипотенузы можно найти по формуле: гипотенуза = катет / cos(угол).
Какое значение может иметь длина гипотенузы треугольника abc, если она равна корню из 2 см?
Значение длины гипотенузы треугольника может быть только положительным, поэтому в данном случае значение длины гипотенузы будет примерно 1.41 см. Точное значение - корень из 2, что примерно равно 1.41 см.