Вселенная оживает многообразием форм. Каждый ее элемент, будь то растение, животное, или объект искусства, обладает своей неповторимой геометрией. В основе этих форм лежит великолепное явление природы, известное как гомотетия - уникальная трансформация, которая переводит одну форму в другую, сохраняя при этом их подобие.
Как же произойдет это невероятное преобразование? Представьте себе, что на глазах у вас неприметная фигура, напоминающая карандаш. Вы нежно надавливаете на ее одинаковые стороны, и волшебство начинает происходить. Ваш карандаш начинает вытягиваться, растягиваться и преобразовываться в нечто новое, но все еще сохраняющее ту же самую основную форму. Это и есть гомотетия - скрытая сила, которая позволяет объектам изменяться, но оставаться верными своему происхождению.
Гомотетия - это одно из удивительных открытий, сделанных учеными в их стремлении понять и описать окружающий мир. Она стала ключевым понятием в геометрии и графике. Благодаря гомотетии мы можем понять, почему одни объекты выглядят похожими, а другие - совсем отличными. Она позволяет нам разглядеть в фигурах искусства и символах жизни неразрывную связь и подобие, несмотря на все различия. Ведь в конечном счете, все они происходят от одного источника - от древних времен до наших дней, от уникальной окружности до множества удивительных окружностей.
Геометрическое преобразование, которое меняет размер и форму окружности
Этот раздел посвящен удивительному геометрическому процессу, который позволяет изменить размер и форму окружности, при этом ее геометрические свойства сохраняются. Это преобразование называется гомотетией, и оно может быть полезным инструментом в изучении и применении геометрии.
Гомотетия является понятием, которое описывает масштабное преобразование геометрической фигуры. При гомотетии окружность может быть увеличена или уменьшена по размеру, сохраняя при этом свою форму и симметричность. Используя синонимы, можно сказать, что гомотетия превращает окружность в другую окружность, которая имеет аналогичную структуру, но различается своим масштабом.
Важным свойством гомотетии является то, что центральная точка, относительно которой производится преобразование, остается неизменной. Это означает, что окружность до и после гомотетии имеют одну и ту же середину. Также радиусы окружностей изменяются с одним и тем же коэффициентом, который определяет масштаб преобразования.
- Гомотетия может быть использована в различных областях, таких как архитектура, дизайн и геодезия.
- Основные свойства гомотетии позволяют применять ее в задачах вычислительной геометрии.
- Обратная гомотетия является тоже гомотетией с другим коэффициентом, позволяющей вернуться к исходной окружности.
Гомотетия и ее связь с кругом
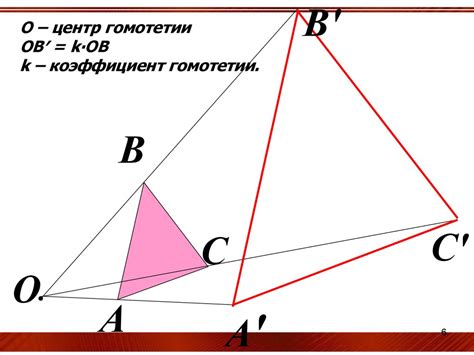
Известно, что гомотетия может быть описана как преобразование, при котором для каждой точки фигуры с центром в данной точке и коэффициентом пропорции заданного числа происходит ее перемещение. Такое преобразование сохраняет все углы между прямыми и пропорции длин отрезков, а также сохраняет форму фигуры.
Круг, несомненно, является особой фигурой. Он имеет бесконечное количество точек, расположенных на одинаковом расстоянии от центра, и сохраняет свою форму при любой гомотетии. То есть, если применить гомотетию к окружности с центром в точке и удерживать пропорцию радиуса окружности к преобразованию коэффициента, получится другая окружность - гомотетия окружности.
Связь между гомотетией и кругом проявляется во многих областях, в том числе геометрии, физике и искусстве. Это важное понятие позволяет нам понять и объяснить преобразование фигур и их взаимосвязи. Правильное понимание гомотетии и ее связи с кругом помогает нам строить сложные конструкции и выявлять законы, заложенные в устройстве нашей плоской реальности.
Математическое определение и свойства гомотетии

Гомотетия можно представить как масштабирование фигуры - все ее точки увеличиваются или уменьшаются пропорционально относительно одного центра. Она может быть применена к различным объектам, в том числе к фигурам любой формы: треугольникам, четырехугольникам, многоугольникам и, конечно, окружностям.
Основные свойства гомотетии связаны с ее влиянием на размер и расположение точек внутри фигуры. При увеличении (или уменьшении) фигуры, расстояния между ее точками изменяются пропорционально фактору гомотетии. Также гомотетия сохраняет все прямые линии внутри фигуры, но не обязательно сохраняет углы между ними. Однако гомотетия всегда сохраняет отношение длин прямых отрезков, проходящих через ее центр.
Важным свойством гомотетии является то, что она обладает центром гомотетии. Этот центр является геометрическим центром масштабирования и определяет направление и степень изменения размеров фигуры. Гомотетия также имеет коэффициент гомотетии, который отражает искажение размеров при масштабировании.
Шаги построения гомотетии: общая идея

- Выберите исходный круг и определите его центр.
- Укажите точку, которая будет служить центром гомотетии.
- Используя циркуль, проведите окружность с центром в точке гомотетии и проходящую через центр исходного круга.
- Найдите точку на окружности гомотетии, расстояние до которой от центра исходного круга будет в необходимом отношении к радиусу исходного круга. Установите радиус величиной, соответствующей этому отношению.
- Повторите шаги 3-4 для получения нового круга с нужными размерами и расположением.
Таким образом, последовательное выполнение этих шагов позволит осуществить гомотетию и преобразовать исходный круг в новый круг с сохранением пропорций. Этот метод можно использовать для моделирования гомотетии в различных задачах, где требуется изменение размера и формы объектов.
Примеры гомотетии в реальной жизни

Архитектура:
Гомотетия находит широкое применение в архитектуре, где позволяет создавать уникальные проекты, объединяющие различные масштабы и формы. Благодаря гомотетическим преобразованиям можно создавать здания и сооружения, которые визуально сливаются с окружающей средой, сохраняя при этом свою идентичность и уникальность формы.
Дизайн:
Принцип гомотетии широко используется в дизайне, как принцип управления пропорциями объектов и элементов на различных масштабах. Он позволяет создавать гармоничные и сбалансированные композиции, где размеры и формы объектов подчиняются определенным соотношениям. Гомотетическое преобразование в дизайне помогает создать визуальную ритмику и единство в композиции.
Биология:
Гомотетия играет важную роль в биологии, где является одним из основных принципов роста и развития живых организмов. Она позволяет организмам расти и менять свой размер, сохраняя при этом пропорции и структуру. Например, гомотетия используется для объяснения пропорционального роста тела человека во время его развития от рождения до взрослого состояния.
Приведенные примеры показывают, что гомотетия является универсальным принципом, который находит применение в различных областях. Она позволяет создавать изначально пропорциональные и гармоничные структуры, а также осуществлять изменение размеров объектов при сохранении их формы и структуры.
Методы доказательства гомотетии: ознакомление с разными подходами

В данном разделе представлено описание двух методов доказательства гомотетии, которые позволяют установить отношение подобия между фигурами без использования прямых определений. Мы охарактеризуем каждый метод и объясним, как они позволяют увидеть преобразование, похожее на превращение окружности в другую окружность. Познакомимся с ключевыми идеями каждого из методов и рассмотрим конкретные примеры, чтобы наглядно иллюстрировать их применение.
Метод 1: Аналитический подходПри помощи данного метода мы будем использовать аналитическую геометрию для доказательства гомотетии. Он основан на использовании алгебраических уравнений и координатных преобразований. Мы рассмотрим, как определить коэффициент масштабирования и центр гомотетии, а также как проверить, что гомотетия сохраняет отношение подобия фигур. | Метод 2: Геометрический подходВторой метод основан на геометрических свойствах фигур и использовании конструктивных операций. Мы будем исследовать геометрические преобразования, такие как построение центра гомотетии при помощи параллельных линий и подобия треугольников. Благодаря этому подходу мы сможем доказать, что фигуры являются подобными исходя из их свойств и установить подходящий масштабирующий коэффициент. |
В итоге, ознакомившись с двумя методами доказательства гомотетии, мы сможем лучше понять, как устанавливается подобие между фигурами и каким образом окружность может быть преобразована в другую окружность. Знание этих методов позволит нам оперативно применять гомотетию в решении геометрических задач и более глубоко изучать подобные трансформации в дальнейшем.
Воплощение симметрии: приобретение формы

Покажем на примере, как предмет, обладающий уникальными особенностями, может преобразиться, отражая в себе суть гомотетии. Рассмотрим случай, когда зыбучие пески принимают форму идеального круга, а затем вновь возвращаются в свою первоначальную форму.
Начальное состояние:
| Промежуточное состояние:
| Конечное состояние:
|
Мы исследуем механизмы, по которым каждая отдельная зернышка песка смещается и взаимодействует с остальными, чтобы образовать новую структуру и затем восстановить первоначальную. Подробно рассмотрим каждый шаг процесса и применим синонимы для описания особенностей и перемен, которые происходят в процессе превращения. Это позволит нам полностью охватить и понять все сложности и уникальные качества данных преобразований.
Вопрос-ответ

Что такое гомотетия?
Гомотетия - это преобразование, при котором каждая точка фигуры увеличивается или уменьшается в одно и то же число раз относительно одной точки, называемой центром гомотетии.
Как доказать, что окружность может быть превращена в окружность с помощью гомотетии?
Для доказательства этого факта необходимо найти центр гомотетии, относительно которого будут изменяться радиус и положение окружности, и показать, что все точки окружности подчиняются правилу изменения размеров и положения.
Существует ли только один способ превращения окружности в окружность гомотетией?
Нет, существует бесконечно много способов превратить окружность в окружность с помощью гомотетии. Все эти способы отличаются выбором центра гомотетии и коэффициента масштабирования.
Как связан радиус и центр гомотетии при превращении окружности в окружность с помощью гомотетии?
Центр гомотетии будет находиться на линии, проходящей через центр исходной и целевой окружностей. Расстояние от центра гомотетии до центра исходной окружности определяет коэффициент масштабирования.
Каким образом гомотетия может быть полезна в геометрии и практическом применении?
Гомотетические преобразования широко используются в геометрии для упрощения задач и построений. Они также имеют практическое применение при масштабировании изображений, создании оптических линз и дизайне предметов с разными размерами.
Как доказать, что гомотетия может превратить окружность в окружность?
Доказательство гомотетии, превращающей окружность в окружность, основывается на простых геометрических свойствах. Пусть дана исходная окружность с центром O и радиусом r, и некоторая точка A вне этой окружности. Пусть также дан коэффициент гомотетии k. Для построения нужно построить две прямые, проходящие через точку A и центр окружности O, и провести две окружности с центром в точке A и центром в O. Если мы можем доказать, что прямые и окружности пересекаются в двух точках B и C, таких что OC = k*OB, то это будет означать, что преобразование является гомотетией.



