Весь мир, весь наш широкий мир, состоит из простых геометрических форм и фигур. Одной из самых основных форм в этой геометрии является прямая, самая простая и наилегчайшая в понимании цельной конструкции. И всегда есть точка, безусловная точка, которую мы мило называем внешним пространством. Что же происходит, когда эти два элемента, прямая и точка в нее, существуют вместе? Как можно доказать, что они обязательно пересекаются? Это вопрос важен и затронет сердца всех тех, кто осмысляет геометрическую теорию и старается узнать глубину истины о нашем математическом мире.
Подводя идеи к доказательству неизбежного пересечения прямой и точки вне нее, нельзя не отметить важность такого условия, которое оно непременно предъявляет. Необходимость стимулирует наш ум и заставляет изучить все возможные сценарии этого смычения, чтобы обеспечить прочность и последовательность описываемых методикой. От простейшего анализа до более сложного, мы должны учиться видеть эту связь между ними, в то же время позволяя себе увидеть больше, чем обычно принято считать возможным.
Акцентируя внимание на методике расчета, мы придаем этому процессу четкость и стройность. Необходимо иметь систему проводимых операций и шагов, позволяющих получить конкретные результаты и развивать мышление в нужном направлении. Только таким образом мы сможем сделать наше доказательство достаточно мощным и захватывающим для всех, кто интересуется геометрией и стремится расширить свои познания в этой области знаний.
Понятие взаимодействия между прямой и точкой
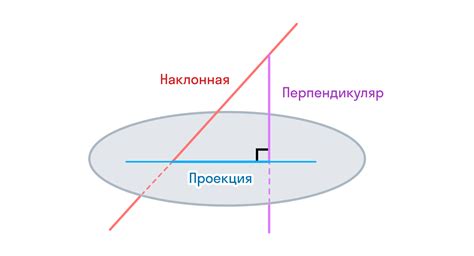
В этом разделе рассмотрим важную концепцию, касающуюся ситуаций, когда прямая и точка вступают во взаимодействие. Изучение таких ситуаций позволяет более глубоко понять и анализировать свойства прямых и точек.
Взаимодействие между прямой и точкой представляет собой простое, но важное понятие в геометрии. Оно описывает ситуацию, когда точка расположена в некоторой пространственной близости к прямой, и может быть связана с ней различными способами.
Значимость точки разделения прямой при ее расположении снаружи
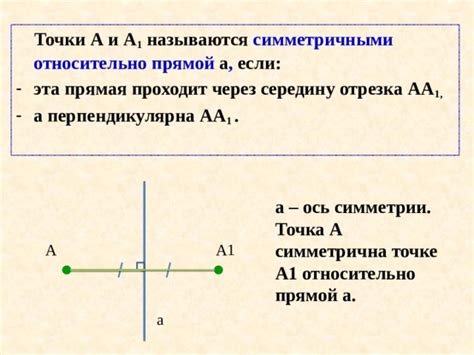
Одним из методов рассмотрения пересечения прямой через точку снаружи является использование векторных операций и операций скалярного произведения. Эти методы позволяют более точно определить положение точки относительно прямой и выявить характеристики их отношений. Кроме того, такой подход позволяет более точно определить и рассчитать необходимые координаты и параметры прямой, используя информацию о точке пересечения.
Необходимое предварительное условие для обнаружения пересечения прямой с точкой находящейся вне ее
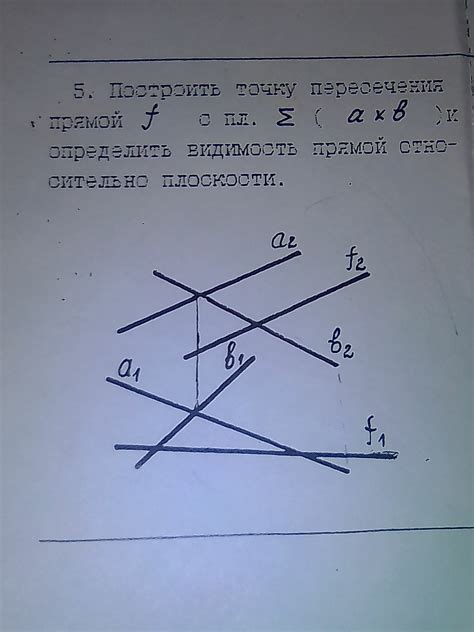
Одним из ключевых понятий является принадлежность точки к прямой. Если точка не принадлежит прямой, то ее координаты или другие характеристики должны удовлетворять особому предварительному условию для обнаружения пересечения прямой с данной точкой. Это условие может быть выражено через сравнение значений координат или использование формул в геометрии и алгебре.
Важно понимать, что это условие является необходимым, но не достаточным для гарантированного обнаружения пересечения между прямой и точкой вне ее. Дополнительные проверки и вычисления могут потребоваться для более точных результатов. Однако, знание и использование этого предварительного условия играет важную роль в определении возможности пересечения прямой с точкой вне ее и направляет последующий анализ в нужном направлении.
Возможные способы подтверждения точки пересечения на плоскости

В данном разделе мы рассмотрим различные методы, которые могут быть использованы для выявления факта пересечения прямых. В ходе исследования таких вопросов, иногда бывает полезно знать различные подходы для подтверждения пересечения двух линий на плоскости. В данном разделе рассмотрим несколько из таких методов.
- Метод анализа коэффициентов прямых: Если известны коэффициенты уравнений двух прямых, то их пересечение можно определить путем сравнения и анализа величин этих коэффициентов. Этот метод позволяет установить, существует ли точка пересечения двух прямых, основываясь на значениях коэффициентов уравнений.
- Графический метод: Один из самых простых и наглядных способов подтверждения пересечения прямых на плоскости. Он основан на построении графиков уравнений прямых и их последующем анализе. Если построенные графики секутся, это будет служить доказательством пересечения данных прямых.
- Аналитический метод: Этот метод требует использования уравнений прямых. Для подтверждения пересечения используется сравнение значений координат точек, лежащих на данных прямых. Если найдется хотя бы одна общая точка у данных прямых, это будет означать их пересечение.
- Метод перебора: Во многих заданиях на доказательство пересечения прямых возможно использование метода перебора, при котором мы исследуем различные точки и подставляем их координаты в уравнения прямых. Если при подстановке выбранных координат получаем одинаковые значения, то это будет свидетельствовать о пересечении данных прямых.
Каждый из этих способов имеет свои особенности и может быть применен в различных ситуациях. Выбор подходящего метода зависит от условий задачи и имеющихся данных. Этот раздел поможет вам разобраться с различными методами подтверждения пересечения прямых на плоскости и применить их на практике.
Расчет координат точки пересечения: методология и основные принципы
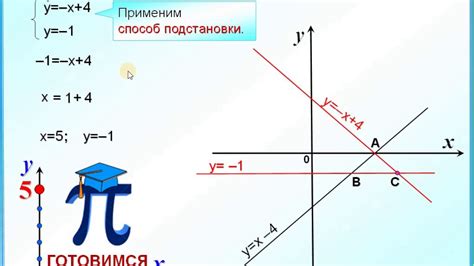
В данном разделе мы рассмотрим методику расчета координат точки пересечения двух линий или кривых. В процессе анализа с использованием геометрических и математических подходов, мы определим необходимые шаги и формулы для получения аккуратных и точных результатов.
Для наглядности и понимания принципов расчета, предлагаем следовать представленному ниже порядку действий:
- Определение уравнений двух линий или кривых, которые предположительно пересекаются. Для этого необходимо рассмотреть характерные свойства графиков и использовать соответствующие модели расчета.
- Выражение переменных и параметров, присутствующих в уравнениях, через известные значения. Это позволит сформулировать систему уравнений, включающую все необходимые параметры для определения точки пересечения.
- Решение системы уравнений с использованием метода подстановки, метода Крамера или других математических алгоритмов. Это позволит найти значения переменных, соответствующие координатам точки пересечения.
- Проверка полученных результатов на корректность и соответствие заданным условиям. В случае необходимости, можно использовать дополнительные методы проверки, такие как графическое представление или дифференциальные вычисления.
Применение данной методики позволяет определить координаты точки пересечения в задачах, где необходимо проанализировать взаимодействие линий или кривых, и получить достоверные результаты в соответствии с предложенными моделями расчета. Используя описанный порядок действий и математические методы, можно получить точные координаты, которые будут полезны при решении различных задач из разных областей научных и технических исследований.
Использование уравнения прямой для доказательства

Перед началом изучения различных приемов и методов доказательства с использованием уравнения прямой, необходимо иметь представление о его общей структуре и свойствах. Уравнение прямой определяет графическую модель, представляющую собой множество всех точек плоскости, удовлетворяющих данному условию.
- Важной частью работы с уравнением прямой является определение ее наклона. Наклон прямой описывает ее отношение к оси координат и позволяет анализировать ее положение в пространстве.
- Еще одним важным понятием является точка пересечения двух прямых. Зная уравнения двух прямых, можно найти их точку пересечения, что позволяет доказать или опровергнуть различные геометрические утверждения.
- Также уравнение прямой позволяет определить расстояние от любой точки до нее, что является полезным инструментом при доказательстве различных свойств.
Использование уравнения прямой для доказательства позволяет строить логическую цепочку рассуждений и анализировать геометрические объекты с точки зрения алгебраического представления. Знание основных свойств и методов работы с уравнением прямой является необходимым условием для успешного доказательства различных утверждений и решения геометрических задач.
Примеры практического применения методики вычислений

В этом разделе представлены разнообразные примеры использования методики расчета, которая позволяет определить возможное пересечение линии через заданную точку вне нее. Разные области знаний и сферы применения требуют анализа и вычислений для достижения конкретных результатов.
- Пример из геодезии: вычисление точки пересечения двух отвесных линий для построения опорной сетки в геодезических работах.
- Пример из физики: определение точки пересечения падающего луча света с поверхностью зеркала или линзы для расчета траектории отраженного или преломленного луча.
- Пример из робототехники: определение пересечения траектории движения робота с заданной точкой, чтобы исключить столкновения и обеспечить безопасность.
- Пример из строительства: расчет точки пересечения двух строительных плоскостей для определения места соединения или разделения элементов конструкций.
- Пример из анализа данных: использование методики расчета для определения точки пересечения графиков функций при исследовании зависимостей и трендов.
Эти примеры являются лишь небольшой частью областей, где методика расчета пересечения линий через заданную точку находит свое применение. Точные исследования, грамотный выбор методов вычислений и анализа помогают достичь точности, надежности и успешного решения поставленных задач в различных областях.
Математические основы выведения заключений

В данном разделе рассматриваются методы общего характера, которые позволяют строить верные и логически обоснованные рассуждения, не ограничиваясь конкретными определениями и задачами.
Математические основы доказательства направлены на развитие навыков логического мышления, анализа проблемных ситуаций и формирования способности к аргументации. В ходе изучения данного раздела исследователи осваивают различные подходы к выведению новых фактов на основе имеющихся.
Кроме того, важным моментом в разделе "Математические основы доказательства" является использование формальных методов и нотаций, позволяющих более точно и ясно выражать математические выкладки и рассуждения. Понимание этих методов и нотаций помогает исследователям преодолевать сложности и повышать точность в выведении математических заключений.
Вопрос-ответ

Какие методы используются для доказательства пересечения прямой через точку вне нее?
Для доказательства пересечения прямой через точку вне нее можно использовать методы координатной геометрии, такие как аналитический метод и геометрический метод.
Какой результат можно получить при доказательстве пересечения прямой через точку вне нее?
Результатом доказательства будет явное указание того, что прямая и точка действительно пересекаются. Это доказывает, что точка не лежит на прямой, а имеет с ней общую точку пересечения.
Какие условия должны выполняться для доказательства пересечения прямой через точку вне нее?
Необходимым условием для доказательства пересечения прямой через точку вне нее является то, что координаты прямой и точки должны быть заданы. Также важно учитывать, что прямая и точка должны находиться в одной плоскости.



