Представьте себе ситуацию: вы стоите перед четырехугольником, каждая сторона которого обозначена вектором. Изучая данную геометрическую фигуру, вы задаетесь вопросом: действительно ли длины векторов, соответствующие сторонам параллелограмма, равны между собой? Если ответ положителен, то как это можно доказать? Ответы на подобные вопросы могут помочь углубить наши знания в области математики и геометрии.
В данной статье мы затронем область геометрии, изучающую деформационные преобразования и отношения между векторами в параллелограммах. В частности, мы сосредоточимся на установлении равенства длин векторов в параллелограмме ABCD.
Для начала необходимо понять, что такое деформационные преобразования и почему они играют важную роль в геометрии. Деформационное преобразование - это способ изменения фигуры без изменения ее размеров, то есть длин всех ее сторон. В параллелограммах деформационные преобразования могут быть представлены в виде смещений, поворотов и отражений.
Что такое параллелограмм и прототипы параллелограммов
В данном разделе рассмотрим понятие параллелограмма, его основные свойства и прототипы, которые лежат в основе его определения. Векторы, перпендикулярные сторонам параллелограмма, играют важную роль при доказательстве равенства длин его сторон.
Определение параллелограмма Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны. Главное свойство параллелограмма заключается в том, что его противоположные стороны равны и параллельны друг другу. Это следует из определения и является основой для доказательства равенства длин векторов в параллелограмме. | Прототипы параллелограммов Для понимания параллелограмма важно рассмотреть его прототипы - фигуры, которые служат основой для его конструкции и свойств. Самостоятельные редактирование Прототипами параллелограммов являются такие фигуры, как прямоугольник, квадрат и ромб. Эти фигуры также обладают свойством параллелограмма - у них противоположные стороны параллельны и равны. |
Понятие "параллелограмм" и его основные характеристики

Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Он также имеет две парами равных и параллельных сторон.
Важными свойствами параллелограмма являются:
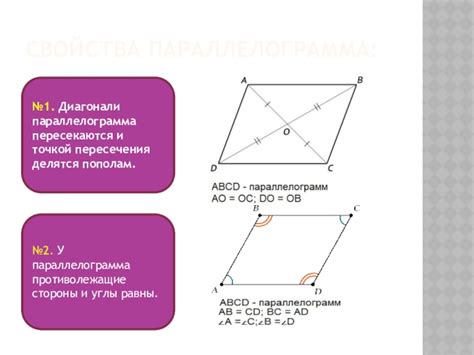
- Противоположные стороны параллельны: Это означает, что если взять две противоположные стороны параллелограмма и продолжить их, то они никогда не пересекутся. Они будут всегда оставаться параллельными друг другу.
- Противоположные стороны равны: Это означает, что длины противоположных сторон параллелограмма равны. Это свойство позволяет нам утверждать о равенстве длин векторов, образованных этими сторонами.
- Углы параллелограмма: Параллелограмм имеет две пары параллельных сторон, что позволяет нам говорить о существовании двух параллельных углов. Эти углы называются соответственно внутренними и внешними углами параллелограмма.
- Диагонали параллелограмма: Диагонали параллелограмма делят его на два треугольника, которые имеют одинаковую площадь. При этом, длина диагоналей может отличаться.
Эти основные свойства параллелограмма дают нам возможность более глубоко изучить и понять его структуру и характеристики. Понимание этих свойств позволяет также проводить различные доказательства и рассуждения в контексте равенства длин векторов в параллелограмме.
Примеры параллелограммов в природе и повседневной жизни

Помимо абстрактных математических понятий, параллелограммы можно найти и в реальном мире. Эта геометрическая фигура широко распространена в природе, а также в повседневной жизни. В данном разделе рассмотрим несколько интересных примеров параллелограммов, которые можно встретить вокруг себя.
- Животный мир: в природе можно наблюдать множество животных, у которых форма их тела или крыльев напоминает параллелограмм. Некоторые виды рыб, например, ангел, обладают спинными плавниками, имеющими форму параллелограмма. Это позволяет им легко перемещаться по воде и сохранять устойчивость в пространстве.
- Растения: в растительном мире также могут встречаться примеры параллелограммов. Например, листья некоторых деревьев, таких как клен или ивовые, имеют форму параллелограмма. Это обеспечивает оптимальное распределение солнечного света на поверхности листа, а также улучшает процесс фотосинтеза.
- Архитектура: параллелограммы можно обнаружить в различных архитектурных сооружениях. Например, некоторые знаменитые мосты, такие как Бруклинский мост, имеют параллелограммальную форму. Это помогает им в равномерном распределении нагрузки и обеспечивает прочность и устойчивость сооружения.
- Дизайн: в дизайне и искусстве также можно использовать параллелограммы, чтобы создать визуально привлекательные композиции. Например, при создании логотипов или графиков часто используются геометрические фигуры, в том числе параллелограммы. Это помогает уравновесить и структурировать визуальные элементы, создавая гармоничный образ.
Это всего лишь некоторые примеры параллелограммов, которые можно встретить в природе и повседневной жизни. Использование данной геометрической фигуры в различных областях подчеркивает ее универсальность и важность в понимании пространственных отношений.
Разнообразие параллелограммов в геометрии и алгебре
Параллелограммы, как их название подразумевает, обладают свойством того, что противоположные стороны параллельны. Это позволяет выполнять различные операции с ними, такие как вычисление площади, определение длин сторон, нахождение углов и многое другое.
Одним из наиболее широко известных параллелограммов является прямоугольник, у которого все углы равны 90 градусам. Это свойство делает прямоугольник особенно полезным в геометрии и позволяет использовать его в различных задачах, связанных с расчетами и построениями.
Кроме того, существуют другие параллелограммы, такие как ромб, у которого все стороны равны, и квадрат, который является одновременно и прямоугольником, и ромбом. Эти фигуры имеют свои особенности и позволяют решать разнообразные задачи в геометрии и алгебре.
Также стоит отметить, что параллелограммы могут быть как плоскими, так и пространственными. Это открывает еще большие возможности для исследования и применения данных фигур в различных областях математики и физики.
Таким образом, разнообразие параллелограммов в геометрии и алгебре представляет интерес для исследователей и практикующих математиков, их свойства и особенности активно применяются в решении различных задач и построении моделей в различных научных областях.
Сопоставление длин направляющих векторов в параллелограммной фигуре и способы его доказательства
Разложение векторов на компоненты, сопоставление значений и анализ геометрических свойств параллелограмма позволяют доказать равенство длин данных векторов. Одним из способов доказательства является сопоставление похожих треугольников, содержащих стороны параллелограмма и соответствующие направляющие векторы.
Другим универсальным методом доказательства равенства длин векторов является использование аналитической геометрии и координатных преобразований. Введение координат в пространстве позволяет записать координаты точек, определяющих концы векторов, и использовать свойства операций с векторами (сложение, вычитание, умножение на скаляр) для доказательства их равенства.
Основные формулы и утверждения, связанные с параллелограммами

Рассматривая параллелограммы, мы можем обнаружить ряд важных формул и теорем, которые позволяют нам легче анализировать их свойства и связи с другими геометрическими фигурами.
Один из фундаментальных результатов, связанных с параллелограммами, - это теорема об углах в параллелограмме. Согласно этой теореме, сумма противоположных углов в параллелограмме равна 180 градусам.
| Теорема | Формулировка |
|---|---|
| Теорема о средних пропорциях | Если в параллелограмме каждая из диагоналей делит его на две равные площади, то эти диагонали взаимно делимы пополам. |
| Теорема о средней линии | Средняя линия параллелограмма равна половине суммы его диагоналей. |
| Теорема об определителе | Площадь параллелограмма равна модулю определителя, построенного на его векторах. |
| Теорема о сумме квадратов сторон | Сумма квадратов длин сторон параллелограмма равна сумме квадратов его диагоналей. |
Эти основные формулы и утверждения обладают большим смысловым значением, а также играют важную роль в решении задач и геометрических доказательствах, связанных с параллелограммами.
Способы подтверждения равенства размеров векторов в геометрической фигуре
В данном разделе рассмотрим несколько методов, позволяющих убедиться в равенстве длин векторов в особой фигуре, образованной соединением точек. При этом будут использованы различные синонимы для обозначения этой геометрической формы.
Во-первых, можно использовать метод равенства сторон, чтобы убедиться, что все четыре стороны данной геометрической фигуры имеют одинаковую длину. Это можно сделать, измерив длину каждой стороны с помощью математических вычислений или используя специальные редакторы для измерения длин отрезков на компьютере.
Во-вторых, можно применить метод проверки диагоналей, чтобы убедиться, что их длины также равны. Обычно эти диагонали являются прямыми линиями, проходящими через центр фигуры и соединяющими противоположные углы. Для измерения длины диагоналей можно использовать геометрические формулы или произвести измерения на чертеже с помощью линейки или других инструментов.
Наконец, можно применить метод равенства углов. В данном случае необходимо учитывать, что все углы в фигуре должны быть равными, чтобы убедиться в равенстве длин векторов. С помощью геометрических вычислений или специальных инструментов для измерения углов можно подтвердить соответствие данному условию.
Геометрическое подтверждение совпадения размеров направленных отрезков
В данном разделе представлено изящное геометрическое доказательство факта равенства длин векторов, не используя специфическую терминологию. Мы рассмотрим свойство параллелограммов и проиллюстрируем, как оно может быть применено для доказательства сопряженности размеров направленных отрезков в данном контексте.
- Взглянем на параллелограмм ABCD и обратим внимание на его особенность - две пары противоположных сторон попарно параллельны.
- Заметим, что отрезки AB и CD являются диагоналями параллелограмма.
- Рассмотрим отрезок AD, который является высотой параллелограмма, опущенной из вершины A на сторону BC.
- Исследуем треугольник ACD, образованный диагональю и высотой параллелограмма.
- Установим, что треугольник ACD является прямоугольным, так как сторона AD перпендикулярна стороне BC (в силу свойства параллелограмма).
- Заметим, что в прямоугольном треугольнике длина гипотенузы равна корню суммы квадратов длин катетов.
- Применим это свойство к треугольнику ACD: длина гипотенузы равна длине отрезка AC, а длины катетов равны длинам отрезков AD и CD соответственно.
- Таким образом, получаем, что длина отрезка AC совпадает с суммой длин отрезков AD и CD.
- Из симметричности параллелограмма следует, что отрезок BD также имеет ту же длину, что и отрезок AC.
- Таким образом, мы доказали равенство длин векторов AB и CD, а также длин векторов AC и BD, используя геометрические свойства параллелограмма и его высоту.
Алгебраическое доказательство эквивалентности длин векторов в параллелограмме

В данном разделе мы рассмотрим метод алгебраического доказательства равенства длин векторов в параллелограмме. Этот метод основан на использовании алгебраических операций и свойств векторов, и позволяет подтвердить полученные геометрические результаты.
Основная идея алгебраического доказательства заключается в преобразованиях векторных уравнений и явном выражении координат векторов с использованием алгебраических операций, таких как сложение и умножение. Параллелограмм, как геометрическая фигура, описывается векторами своих сторон и диагоналей. Наша задача - показать, что длины этих векторов равны друг другу.
Для начала, мы определимся с обозначениями и введем переменные, которые будут описывать векторы в параллелограмме. Затем, используя свойства векторов и операции алгебры, мы разложим векторы на составляющие и выражения в координатах. После этого, мы приступим к сравнению и алгебраическому преобразованию уравнений, чтобы получить равенство длин векторов.
Необходимо отметить, что алгебраическое доказательство равенства длин векторов в параллелограмме является одним из методов и может быть использовано в сочетании с другими геометрическими методами для подтверждения и углубления понимания этого геометрического свойства.
Вопрос-ответ

Как доказать равенство длин векторов в параллелограмме abcd?
Чтобы доказать равенство длин векторов в параллелограмме abcd, можно воспользоваться свойствами параллелограмма. Одно из этих свойств гласит, что в параллелограмме противоположные стороны равны по длине. Таким образом, достаточно доказать, что вектор AB равен вектору DC и вектор AD равен вектору BC.
Какие свойства параллелограмма помогут доказать равенство длин векторов в параллелограмме abcd?
В параллелограмме abcd можно использовать свойства равенства противоположных сторон и равенства диагоналей. Свойство равенства противоположных сторон утверждает, что сторона AB равна стороне DC, а сторона AD равна стороне BC. Свойство равенства диагоналей гласит, что диагонали AC и BD равны между собой.
Можно ли доказать равенство длин векторов в параллелограмме abcd без использования свойств параллелограмма?
Да, равенство длин векторов в параллелограмме abcd можно доказать и без использования свойств параллелограмма. Можно воспользоваться теоремой Пифагора для треугольников ABP и CDP, где P - точка пересечения диагоналей AC и BD. Если длины сторон AB, BP, и PD равны, то это означает равенство длин векторов AB и CD.
Какие еще методы можно использовать для доказательства равенства длин векторов в параллелограмме abcd?
Помимо свойств параллелограмма и теоремы Пифагора, можно воспользоваться геометрическими построениями. Например, можно построить серединные перпендикуляры к сторонам параллелограмма и доказать, что они пересекаются в одной прямой точке. Это означает равенство длин векторов AB и CD, а также AD и BC.
Почему равенство длин векторов в параллелограмме abcd является важным свойством?
Равенство длин векторов в параллелограмме abcd является важным свойством, так как оно позволяет делать выводы о равенстве сторон и диагоналей. Это свойство помогает упрощать геометрические выкладки и решать задачи, связанные с параллелограммами. Кроме того, равенство длин векторов может быть использовано для доказательства других геометрических утверждений.
Как доказать равенство длин векторов в параллелограмме abcd?
Для доказательства равенства длин векторов в параллелограмме abcd можно воспользоваться свойством параллелограмма, согласно которому противоположные стороны параллелограмма равны. Из этого следует, что длина векторов ab и cd равны, а также длина векторов bc и ad равны.