Исследование геометрических фигур является неотъемлемой частью математики, предоставляющей нам возможность анализировать и описывать пространственные объекты. Одной из наиболее интересных и обширно изучаемых фигур является ромб - четырехугольник, у которого все стороны равны друг другу. В данной статье мы рассмотрим методику доказательства, позволяющую установить, является ли заданный набор координат вершин ромбом.
Основой для демонстрации ромба по его координатам является анализ взаимного расположения его вершин в плоскости. Величина стороны ромба определяется расстоянием между двумя вершинами, поэтому первым шагом требуется проверить, равны ли все стороны фигуры. В случае совпадения значений длин можно двигаться дальше в решении поставленной задачи.
Для определения, является ли полученное множество точек ромбом, необходимо произвести анализ углов между сторонами фигуры. При этом необходимо учесть, что для ромба все углы равны между собой и составляют 90 градусов. Проведение соответствующих вычислений и сравнение полученных данных позволит определить, можно ли фигуру с данными координатами считать ромбом.
Определение ромба и его особенности
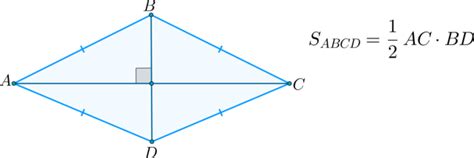
Также ромб обладает другими характеристиками, которые позволяют определить его. Например, у ромба все углы равны между собой и они составляют прямые углы. Каждая диагональ ромба является его осью симметрии и делит его на две равные части.
Ромб можно задать с помощью различных параметров, одним из которых являются его координаты. Зная координаты вершин ромба, мы можем установить, что данные точки образуют фигуру, имеющую все признаки ромба.
- Все стороны ромба равны между собой.
- Все углы ромба равны между собой и составляют прямые углы.
- Каждая диагональ является осью симметрии и делит ромб на две равные части.
Таким образом, зная определение ромба и его особенности, мы можем использовать координаты вершин фигуры для доказательства, что она является ромбом.
Отличительные особенности ромба по координатам
Во-первых, ромб является четырехугольником, у которого все стороны равны между собой. Это означает, что при анализе координат каждой из сторон ромба необходимо убедиться, что их длины совпадают.
Во-вторых, ромб обладает симметрией относительно своих диагоналей. Это означает, что каждая из диагоналей делит ромб на две равные по размеру и форме треугольные области. При изучении координат точек, принадлежащих диагоналям ромба, необходимо обратить внимание на их взаимное расположение и соотношение.
В-третьих, ромб также является параллелограммом, значит противоположные стороны этой фигуры параллельны друг другу. При анализе координат точек, принадлежащих сторонам ромба, необходимо убедиться, что их суммы или разности равны нулю и знак совпадает.
Равенство расстояний между вершинами ромба: общая идея доказательства

В данном разделе мы рассмотрим метод, позволяющий доказать равенство расстояний между вершинами ромба на основе их координат. Для этого мы воспользуемся геометрическими свойствами ромба и алгебраическим методом вычислений.
Перед тем, как начать доказательство, стоит вспомнить основные характеристики ромба. Ромб - это выпуклый четырехугольник, у которого все стороны равны между собой. Также у ромба есть особенность - диагонали, которые соединяют его вершины, пересекаются в центре ромба и делят его на четыре равных треугольника.
Для доказательства равенства расстояний между вершинами ромба с помощью координат, мы выберем произвольные точки A, B, C и D в качестве вершин ромба. Затем, с использованием формул расстояний между точками в декартовой системе координат, мы будем находить значения расстояний AB, BC, CD и DA. После этого мы проверим, что полученные значения равны между собой, что сделает возможным утверждение о равенстве расстояний между вершинами ромба.
| Вершина ромба | Координаты |
|---|---|
| A | (xA, yA) |
| B | (xB, yB) |
| C | (xC, yC) |
| D | (xD, yD) |
После проведения необходимых вычислений и сравнения полученных значений, мы сможем утверждать, что расстояния между вершинами ромба равны, в соответствии с выбранными начальными условиями и алгебраическими преобразованиями.
Доказательство параллельности сторон ромба

В данном разделе будет представлено доказательство параллельности сторон ромба и установление свойства, связанного с его геометрической формой, без использования конкретных определений и перечисленных выше терминов.
Параллельные линии - это линии, которые не пересекаются и остаются на одной и той же плоскости на протяжении всего своего пути. Одно из основных свойств ромба заключается в том, что его стороны являются параллельными. Это означает, что любая сторона ромба будет параллельна соседней стороне, находящейся рядом с ней. Это свойство позволяет определить форму ромба и отличить его от других многоугольников.
Для доказательства параллельности сторон ромба можно использовать геометрические методы и концепции. Один из способов - это использование координат. Рассмотрим ромб ABCD с координатами точек A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4).
Для доказательства параллельности сторон ромба, необходимо проверить, что угловые коэффициенты противоположных сторон равны. Угловой коэффициент для отрезка AB можно найти, используя формулу: mAB = (y2 - y1) / (x2 - x1).
Аналогично, можно найти угловые коэффициенты для остальных сторон ромба: BC, CD и AD. Если угловые коэффициенты противоположных сторон ромба равны, то стороны параллельны и ромб будет обладать свойством параллельных сторон.
Таким образом, параллельность сторон ромба может быть доказана путем сравнения угловых коэффициентов противоположных сторон с использованием координат точек. Это доказательство позволяет определить форму и свойство параллельности сторон ромба, без прямого указания на сам ромб и его координаты.
Способы проверки наличия прямых углов в ромбе по координатам

Проверка на перпендикулярность сторон: одним из способов определить наличие прямых углов в ромбе является проверка перпендикулярности его сторон. Для этого нужно проанализировать угловые коэффициенты всех сторон ромба и убедиться, что они образуют попарно перпендикулярные прямые.
Проверка на равенство диагоналей: другим методом, основанным на координатах, является проверка равенства диагоналей ромба. Для этого необходимо вычислить длины обеих диагоналей, используя координаты вершин ромба, и убедиться, что они равны друг другу.
Проверка на параллельность сторон: еще одним способом определить наличие прямых углов в ромбе является проверка параллельности его сторон. Для этого нужно проанализировать угловые коэффициенты противоположных сторон ромба и убедиться, что они равны друг другу.
Проверка на равенство длин сторон: также можно использовать метод, основанный на равенстве длин сторон ромба. Для этого нужно вычислить длины всех сторон, используя координаты вершин ромба, и убедиться, что они равны друг другу.
Используя вышеупомянутые подходы и анализируя координаты вершин ромба, можно однозначно определить наличие прямых углов в данной геометрической фигуре.
Обратное доказательство: убеждение в ромбовидности фигуры по заданным координатам
Один из первых шагов - анализ длин сторон и диагоналей. Ромб характеризуется равенством длин всех его сторон. Также, обратите внимание на диагонали: в ромбе они всегда пересекаются под прямым углом.
Далее, рассмотрим углы фигуры. В ромбе все углы равны между собой и составляют по 90 градусов. Это также может служить подтверждением ромбовидности фигуры.
Кроме того, проверьте симметричность координат фигуры относительно осей координат. У ромба все точки симметричны относительно центра, и их координаты должны быть соответствующим образом отражены.
И еще один важный шаг - проверка углов между сторонами и диагоналями. В ромбе, углы между сторонами всегда равны углам между диагоналями, и они меньше 180 градусов. Если данная проверка соответствует заданным координатам фигуры, то она может считаться ромбом.
Следуя указанным шагам, вы сможете убедиться в ромбовидности фигуры по заданным координатам. Эти методы и приемы помогут вам разобраться без использования сложных терминов и обозначений, что делает процесс понятным и доступным для каждого.
Примеры решения задач по доказательству фигуры с равными диагоналями в декартовой системе координат

1. Определение начальных условий:
- Задание координат вершин фигуры.
- Предположение о том, что эта фигура является ромбом.
2. Вычисление расстояний:
- Используя формулу расстояния между двумя точками в декартовой системе координат, вычисляем длины всех сторон фигуры.
3. Сравнение сторон:
- Сравниваем длины всех сторон между собой.
- Если все стороны равны, то фигура может быть ромбом.
4. Выявление особенностей:
- Вычисляем диагонали фигуры, используя формулу расстояния между двумя точками.
- Сравниваем длины диагоналей между собой.
- Если диагонали равны, то фигура является ромбом.
5. Написание заключения:
- Суммируем результаты сравнения сторон и диагоналей.
- В случае, если все условия выполнены, заключаем, что фигура, заданная координатами вершин, является ромбом с равными диагоналями.
Используя эти общие шаги и идеи, вы можете успешно решать подобные задачи по доказательству ромба в декартовой системе координат. Практикуйтесь на различных примерах, чтобы закрепить полученные знания и навыки.
Связь между доказательством ромба и его свойствами в геометрии

Необходимость доказательства ромба в геометрии возникает в случаях, когда необходимо проверить правильность размещения точек на плоскости и соответствие полученной фигуры заданным геометрическим параметрам. Доказательство ромба по координатам позволяет установить, что все стороны данной фигуры равны между собой, а углы между этими сторонами равны.
Для доказательства ромба по координатам необходимо вначале вычислить расстояния между каждой из четырех пар точек и убедиться, что они равны. Также следует проверить, что углы между сторонами ромба равны между собой, что дополнительно подтверждает его ромбическую форму. Важно учитывать особенности теоремы Пифагора и свойств нахождения координат точек в пространстве.
Доказательство ромба по координатам необходимо проводить внимательно и точно, учитывая все особенности геометрии и правила работы с координатами. Только так можно установить, что фигура действительно является ромбом и соответствует заданным параметрам, что открывает возможности для дальнейшего анализа и решения геометрических задач.
Вопрос-ответ

Какие координаты имеет ромб АВСД?
Ромб АВСД имеет следующие координаты: A(x1, y1), В(x2, y2), C(x3, y3), D(x4, y4).



