В математике существуют различные функции, которые описывают зависимость между величинами. Одной из таких функций является квадратичная функция, которая характеризуется использованием переменных во второй степени. В данной статье мы рассмотрим одну из таких функций и определим ее значение при заданном значении переменной.
Для начала, давайте определимся с терминологией. Функция – это математическое правило, которое ставит в соответствие каждому элементу из одного множества элемент из другого множества. Значение функции – это результат ее работы при заданном значении переменной.
В нашем случае, рассматриваемая функция представлена квадратичным уравнением вида у = 4х^2. Здесь, х – это переменная, а 4х^2 – это выражение, зависящее от значения переменной.
Теперь, давайте определим значение этой функции при заданной переменной. Пусть х = 3. Для этого мы должны подставить значение переменной вместо х в наше выражение и выполнить соответствующие вычисления.
Понимание функции и ее числовых результатов
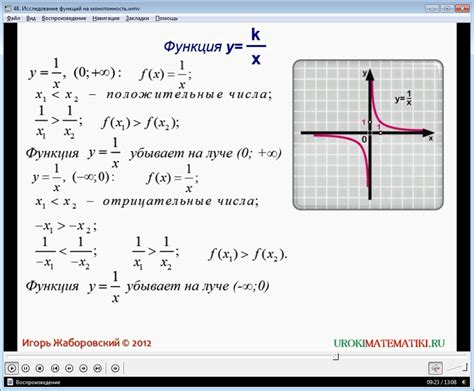
Когда говорят о функции с заданным значением, подразумевается, что для определенного значения аргумента функция принимает определенное числовое значение. Это означает, что при указанном значении аргумента функция вычисляется и возвращает соответствующий результат. Такая функция может быть представлена в виде математического выражения, в котором используется переменная и заданные коэффициенты или операции.
Как определить значение функции для заданного аргумента?

Прежде чем перейти к конкретным методам, важно понять базовое понятие функции и аргумента. Функция представляет собой математическое правило, которое ставит в соответствие каждому элементу из одного множества некоторый элемент из другого множества. Аргумент, в свою очередь, является входным значение функции. Зная определение функции и значение аргумента, мы сможем найти значение функции.
- Метод подстановки – один из основных способов нахождения значения функции. Он заключается в замене аргумента в функции на заданное значение и последующем вычислении значения функции.
- Графический метод – позволяет наглядно определить значение функции для заданного аргумента с помощью графика функции. Находим значение на оси ординат, соответствующей данному аргументу на оси абсцисс.
- Интерполяционные методы – использование интерполяции позволяет приближенно определить значение функции для заданного аргумента, основываясь на уже известных значениях функции в некоторых точках.
- Аппроксимационные методы – позволяют находить значение функции для заданного аргумента на основе аппроксимационной формулы, которая явно или неявно описывает исходную функцию.
- Аналитические методы – использование аналитических методов позволяет находить значение функции для заданного аргумента с помощью аналитических преобразований, дифференцирования и интегрирования.
Выбор метода для определения значения функции для заданного аргумента зависит от поставленной задачи, доступных данных и набора инструментов, которыми мы располагаем. В следующих разделах мы рассмотрим подробнее каждый из упомянутых методов и приведем примеры их использования.
Пример: функция y = 4x^2
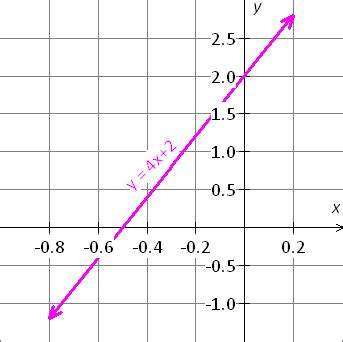
В данном разделе мы рассмотрим конкретный пример функции вида y = 4x^2, чтобы увидеть, как она работает и какие результаты она дает. Мы изучим формулу данной функции и разберем, как ее использовать для вычисления значений y в зависимости от заданных значений x. Также мы рассмотрим график функции и проанализируем его особенности.
Решение уравнения: определение значения y при x = 3

В данном разделе рассматривается процесс нахождения значения переменной y при заданном значении x, используя заданную функцию и уравнение. Значение y определяется путем подстановки значения x в функцию и проведения несложных математических операций.
- Шаг 1: Определение функции.
- Шаг 2: Замена переменной x на заданное значение.
- Шаг 3: Выполнение операций для нахождения значения y.
Решение уравнения позволяет найти конкретное значение переменной y при известном значении x. Этот процесс может быть применен в разных областях, включая математику, физику и экономику, где знание точного значения переменной необходимо для расчетов и анализа. Используя данную методику, можно быстро определить значение y, что делает ее полезной и эффективной в решении различных задач.
Также стоит отметить, что значения функции y при различных значениях x могут быть использованы для решения практических задач. Например, в физике функция y = 4x^2 может описывать зависимость пути от времени при равномерно ускоренном движении тела. Такая информация может быть полезна при расчете времени прохождения определенного расстояния, а также при прогнозировании результатов экспериментов.
- Практическое применение функции y = 4x^2 включает:
- Расчет площади фигуры при заданном значении x;
- Определение максимального или минимального значения функции;
- Анализ зависимости величины отремонтированной техники от затраченного времени;
- Прогнозирование роста населения в зависимости от года;
- Расчет рентабельности производства при различных объемах производства;
- Моделирование движения тела в плоскости и т.д.
Таким образом, изучение функции y = 4x^2 и ее применение в практических задачах может помочь в решении различных проблем и предсказании результатов в различных областях науки и техники.
Вопрос-ответ

Как выразить х из уравнения у = 4х^2 при у = 48?
Для выражения х из уравнения у = 4х^2 при у = 48, нужно подставить значение у в уравнение и решить получившееся квадратное уравнение.
Какая является функция с заданным значением у = 4х^2 при х = 3?
Функция с заданным значением у = 4х^2 при х = 3 является квадратной функцией с коэффициентом а = 4 и ординатой точки х = 3.
Как найти значение у, если известно значение х и функция у = 4х^2?
Для нахождения значения у, если известно значение х и функция у = 4х^2, необходимо подставить значение х в функцию и выполнить соответствующие математические операции.
Какие значения может принимать функция у = 4х^2, если х может принимать значения от 0 до 10?
Если х может принимать значения от 0 до 10, то функция у = 4х^2 будет принимать значения в диапазоне от 0 до 400.



