В мире математики существует множество функций, которые помогают нам понять зависимости между различными переменными. Одной из таких функций является связь y с двукратным значением x. Вопрос в том, находится ли эта связь в прямой пропорциональности или есть другие закономерности, управляющие изменением значений y при изменении x.
Для того чтобы определить, как взаимосвязаны y и двукратное значение x, необходимо проанализировать их значения и искать закономерности. Возможно, что каждое изменение значения x будет сопровождаться аналогичным изменением значения y в два раза больше. Это может указывать на прямую пропорциональность между двумя переменными.
Однако, существует возможность, что связь между y и двукратным значением x не будет такой простой. Для обнаружения других закономерностей наиболее эффективным методом является графическое представление зависимости между этими переменными. Различные формы графиков могут указывать на более сложные функциональные связи.
Понятие функции с удвоенным аргументом: принадлежит ли оно к категории прямой пропорциональности?

Основная цель данного анализа заключается в определении, может ли такая функция считаться прямой пропорциональностью, основываясь на сущности и свойствах прямой пропорциональности в математике. Важно изучить природу связи между "x" и "y" в этой функции и выяснить, соответствует ли она общему определению прямой пропорциональности.
Проанализировав основные характеристики прямой пропорциональности, такие как постоянное отношение и прямолинейная зависимость между переменными, можно провести сравнение с функцией, описанной в данном контексте. Необходимо выяснить, существует ли пропорциональное отношение между "x" и "y", и можно ли установить постоянный множитель, связывающий эти переменные в данной функции.
Понятие прямой пропорциональности и её особенности

Прямая пропорциональность имеет свои характеристики, которые помогают сформулировать и понять эту зависимость. Во-первых, прямая пропорциональность подразумевает, что при изменении одной переменной величины в два раза, другая переменная также изменится в два раза. Это явление можно наблюдать на графике, где точки образуют прямую линию. Во-вторых, прямая пропорциональность предполагает отсутствие постоянной слагаемой в уравнении, то есть оно имеет вид y = kx, где k - коэффициент пропорциональности. Третья характеристика – это равенство отношений между переменными величинами. Если мы возьмем любые две переменные и их соответствующие значения, отношение этих значений должно быть равно для всех пар переменных величин.
Прямая пропорциональность – это важное понятие в математике и имеет широкое применение в реальном мире. Она позволяет представить зависимость между двумя переменными величинами и использовать её для прогнозирования и анализа данных. Такие примеры можно найти в физике, экономике, статистике и других областях науки и жизни. Понимание прямой пропорциональности и её характеристик помогает увидеть и оценить связи между переменными и применить их для решения различных задач и задачей.
Анализ связи между y и x в функции y = 2x
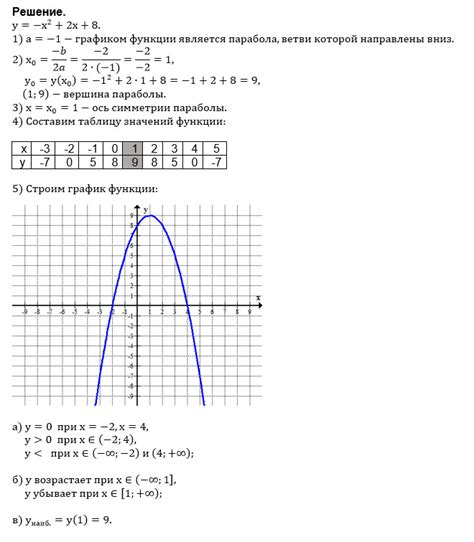
В данном разделе мы рассмотрим связь между величинами y и x в функции y = 2x и проанализируем, соответствует ли эта связь принципам прямой пропорциональности. Будем исследовать, как изменение одной величины влияет на изменение другой, и выявим особенности данной функции.
Для начала, применим метод определения эквивалентности: если при увеличении значения x на единицу, значение y также увеличивается ровно на две единицы, то можно сделать предположение о наличии прямой пропорциональности между этими величинами.
Также нужно обратить внимание на случаи, когда изменение y не соответствует удвоению значения x. В таких случаях можно предположить наличие некоторых иных закономерностей или зависимостей между переменными, не связанных с прямой пропорциональностью.
Анализируя поведение функции y = 2x, мы сможем определить, соответствует ли эта функция принципам прямой пропорциональности или же имеет иные особенности зависимости между переменными y и x. Для этого рассмотрим конкретные значения и проведем подробное исследование в следующих разделах.
Вопрос-ответ

Что такое функция?
Функция - это зависимость между двумя переменными, где каждому значению первой переменной соответствует единственное значение второй переменной.
Что значит "функция y равна двойному значению x"?
Это означает, что значения переменной y в функции равны удвоенным значениям переменной x. Если x равно 2, то y будет равно 4, x=3, y=6 и так далее.
Считается ли такая зависимость между переменными прямой пропорциональностью?
Да, такая зависимость является примером прямой пропорциональности. При увеличении значения x в два раза, значение y также увеличивается в два раза.



