Неоспоримо, среди множества математических терминов есть такие, которые не всегда имеют однозначные определения. Одним из таких понятий является "прямая". Все мы хорошо знакомы с этим термином, но не каждый может точно определить его сущность или это понятие оказывается несколько размытым в нашем сознании. Так какова же правильная основа для понимания и определения концепции "прямой"?
Прежде всего, следует отметить, что понятие "прямой" имеет свои корни в геометрии. И хотя этот термин может быть интерпретирован и в других контекстах, мы сосредоточимся на его геометрическом значении. Прямая – это геометрическая фигура, которая обладает определенными свойствами. Исторически сложилось так, что каждая прямая имеет два конца, которые по своей природе являются экстремальными точками на этой линии.
Однако, стоит задуматься, а имеет ли прямая всегда концы? Может ли существовать исключение, когда эти две точки могут отсутствовать? Это вопрос, который вызывает интерес и непосредственное желание изучить более глубоко данную проблему. Давайте разберемся вместе!
Описание прямой и ее характеристики
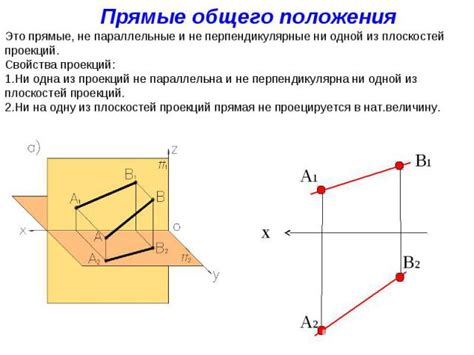
Одно из главных свойств прямой - это то, что она состоит из бесконечного количества точек, которые расположены на одной линии. Каждая точка прямой может быть описана координатами на числовой оси. Прямая также имеет два направления - положительное и отрицательное, которые определяются выбором начальной точки и условных знаков.
Прямую можно описать с помощью уравнения, которое связывает координаты точек, лежащих на ней. Уравнение прямой имеет общую форму y = mx + b, где m - наклон прямой, а b - свободный член, определяющий смещение прямой относительно начала координат. Зная эти параметры, можно провести прямую на графике или рассчитать координаты любой точки, лежащей на ней.
Еще одной важной характеристикой прямой является ее наклон. Наклон определяет угловой коэффициент прямой и показывает, насколько она отклоняется от горизонтального или вертикального положения. Прямая, параллельная оси ординат, имеет бесконечный наклон, а прямая, параллельная оси абсцисс, имеет наклон равный нулю.
| Свойства прямой | Описание |
|---|---|
| Бесконечность | Простирается в бесконечность в обоих направлениях |
| Направление | Имеет положительное и отрицательное направление |
| Уравнение | Описывается уравнением y = mx + b |
| Наклон | Определяет угловой коэффициент прямой |
Определение прямой по двум точкам: ключевой аспект линейной геометрии

В процессе определения прямой по двум точкам, отсутствие прямой вертикальности или горизонтальности это ключевая характеристика. Используя синтаксическую связь между возможно выделенными! Представим, что имеется исходные уникальные значения двух точек на плоскости, и мы хотим найти уравнение прямой, проходящей через эти точки.
Одним из методов определения прямой является использование формулы наклона прямой, которая представляет собой отношение изменения значения y к изменению значения x при движении от одной точки к другой на прямой. Помимо этого, будет рассмотрено применение формулы точки пересечения прямых, позволяющей определить точку пересечения двух прямых по заданным коэффициентам наклона и точкам на этих прямых.
Определение прямой по двум точкам является неотъемлемой частью линейной геометрии и используется в широком спектре геометрических задач. Понимание и применение основных методов и принципов определения прямой по двум точкам позволит решать эти задачи более эффективно и точно.
Существуют ли прямые, у которых нет концов
В данном разделе рассмотрим интересующий вопрос о существовании прямых, которые не имеют определенных концов. Мы проведем анализ и исследование природы прямых линий, обратив внимание на их свойства и характеристики.
При изучении геометрических объектов, таких как прямые линии, важно понимать, что в обычной трехмерной пространственной модели мышление строится на использовании понятий начала и конца для определения границы. Однако, в абстрактной модели прямой мы можем столкнуться с интересным явлением, где отсутствуют установленные концы.
| Свойство | Описание |
|---|---|
| Бесконечность | Прямая может продолжаться в бесконечность в обе стороны без видимой границы, где начало и конец невозможно однозначно определить. |
| Сегменты прямых | В различных конструкциях и задачах мы можем ограничивать прямые определенными сегментами, тем самым создавая ощущение концов. Однако, на самом деле эти сегменты всегда могут быть продолжены в обе стороны. |
| Гипотетические модели | В математических и физических моделях нередко используются прямые, для которых понятие конца является несущественным или искусственно определенным с целью упрощения анализа. |
Таким образом, хотя в обычной трехмерной реальности понятие конца прямой является важным и понятным, в абстрактной модели мы можем рассматривать прямые без жестких конечных границ. Это свойство прямых зачастую используется в математике и других науках для создания гипотетических моделей и упрощения анализа.
Понятие линий с определенными началом и концом и примеры таких линий

Линии с концами можно найти в различных областях, таких как геометрия, инженерия, графический дизайн и другие. Эти линии могут быть представлены как прямые или кривые, и их концы могут быть явно определены или подразумеваться. Важно отметить, что линия с концами всегда имеет определенное начало и конец, которые определяют ее длину и направление.
Примеры линий с определенными началом и концом:
1. Отрезок: Это прямая линия между двумя точками, которая имеет явно определенное начало и конец.
2. Дуга: Дуга - это линия, которая представляет собой фрагмент окружности или эллипса и имеет явно определенную границу в виде начала и конца. Например, часовая стрелка на циферблате имеет начало и конец на окружности.
3. Сегмент: Это часть линии, ограниченная определенными концами, которые явно определяют ее начало и конец. Например, сегмент прямой линии между двумя точками на графике.
Линии с концами являются важными элементами визуального представления и математического анализа. Их правильное использование позволяет более точно определить границы объектов и явления.
Вопрос-ответ

Что такое "прямая концы 5 класс"?
Прямая концы 5 класс - это понятие из области геометрии, которое обозначает отрезок прямой, ограниченный двумя точками.
Как определить концы прямой?
Концы прямой определяются точками, которые являются началом и концом данного отрезка.
Может ли прямая иметь более двух концов?
Нет, прямая может иметь только два конца, так как она представляет собой отрезок, ограниченный этими точками.
Какие свойства имеет прямая с двумя концами?
Прямая с двумя концами обладает такими свойствами, как бесконечность в обоих направлениях, отсутствие изгибов и возможность быть продолженной в обоих направлениях.



