Когда мы рассматриваем отрезок, важно обратить внимание на два ключевых элемента - точку начала и точку конца. Эти точки играют значимую роль в определении и понимании свойств и связей отрезка. Они являются граничными точками, представляющими крайние значения и принимающие на себя особое значение внутри отрезка.
Точка начала отрезка - это первая точка, которая дает отрезку физический смысл и определяет его стартовую точку. Она может быть олицетворением начала пути, пропуском или началом абстрактной последовательности. Важно отметить, что в контексте отрезка точка начала может быть зафиксированной или переменной, что дает отрезку динамичность и возможность изменения.
Точка конца отрезка работает в паре с точкой начала, она устанавливает границу отрезка и определяет его конечную точку. По сути, она закрывает путь или завершает последовательность, отделяет отрезок от остальной части пространства или последовательности, которую он представляет. Также как и точка начала, точка конца может быть фиксированной или изменяющейся в контексте отрезка.
Основные концепции и характеристики отрезка
Важно отметить, что отрезок представляет собой участок прямой, который не имеет наличия ни в одну из сторон за пределами своей начальной и конечной точек. Это позволяет определить его длину, которая является одной из его фундаментальных характеристик. Другим важным свойством отрезка является его ориентация, которая определяется его начальной и конечной точками.
Отрезки могут быть различных длин и ориентации, и в зависимости от их характеристик, могут быть классифицированы как конечные или бесконечные. Конечные отрезки, как следует из названия, имеют определенную длину и ограничены своими конечными точками. Бесконечные отрезки, с другой стороны, простираются бесконечно в одном или обоих направлениях.
Понимание понятия отрезка играет важную роль в решении геометрических задач и моделированию реальных объектов. Отрезки могут быть применены, например, в вычислительной геометрии, чтобы представить плоские или пространственные объекты, а также в анализе данных для визуализации и оценки числовых значений. Поэтому, понимание определения и свойств отрезков является необходимым для развития и применения математической и научной мысли.
Основные характеристики и важные аспекты отрезка

В данном разделе рассмотрим ключевые аспекты и основные характеристики, связанные с геометрическим объектом, который представляет собой часть прямой между двумя точками. Отрезок, как геометрическая фигура, обладает рядом важных свойств, которые играют существенную роль при его изучении и анализе.
Длина отрезка: величина, которая характеризует протяженность отрезка и измеряется в единицах длины. Длина отрезка определяется по формуле, использующей координаты начальной и конечной точек.
Направление отрезка: указывает на порядок расположения начальной и конечной точек друг относительно друга. Отрезок может быть направлен слева направо или справа налево.
Взаимное расположение отрезков: возможные случаи, когда два отрезка пересекаются, не пересекаются или совпадают. Это свойство отрезков имеет важное значение при решении задач, связанных с построением, интервалами и пересечениями.
Принадлежность точек отрезку: говорит о том, лежит ли точка на отрезке, на его продолжении или вне его границ. Данная характеристика позволяет определить, включает ли отрезок данную точку или нет.
Таким образом, понимание определения и основных свойств отрезка является важным для понимания и решения геометрических задач и задач, связанных с изучением пространственного объекта.
Отрезок как геометрическая фигура
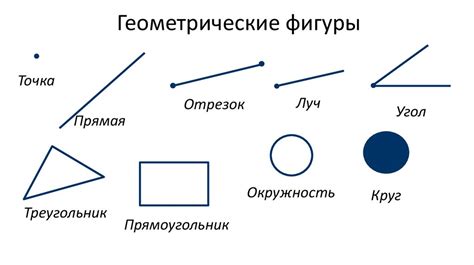
Геометрический отрезок значения приобретает не только в математике, но и во многих других областях науки и промышленности. Отрезки могут служить основой для построения графиков функций, отображения пространства на плоскость, а также для измерения и определения расстояний.
Отрезок характеризуется своей длиной - расстоянием между его начальной и конечной точками. Эта величина может быть измерена с помощью различных инструментов, таких как линейка или специальные приборы.
Важно отметить, что отрезок является сущностью, обладающей свойствами, которые могут быть использованы для анализа и решения задач. К некоторым из них относятся симметричность, параллельность, перпендикулярность и многое другое.
Использование отрезков в геометрии позволяет рассматривать и изучать разнообразные фигуры и их характеристики, а также анализировать их пространственное расположение и взаимодействие друг с другом.
Таким образом, отрезок является одной из основных геометрических фигур, которая имеет широкое применение в различных областях знания и позволяет осуществлять измерения, построения и анализ в пространстве.
Границы отрезка и их значения
Первая граница отрезка, которую мы рассмотрим, это левая граница. Она является точкой начала отрезка и имеет свое значение, которое определяет его положение относительно нулевой точки на числовой прямой. Левая граница может быть как положительной, так и отрицательной, в зависимости от направления отрезка.
Вторая граница отрезка - правая граница, определяющая его конечную точку. Правая граница также имеет свое значение и играет важную роль в определении длины отрезка. Значение правой границы может быть как положительным, так и отрицательным, в зависимости от направления отрезка и его положения на числовой прямой.
Значения границ отрезка могут быть выражены числами или переменными, которые отражают точную позицию начала и конца отрезка. Изучение и анализ значений границ позволяет нам определить длину отрезка, его направление, а также выполнить различные операции на числовой прямой, такие как сложение, вычитание и сравнение длин.
Положение отрезка на координатной плоскости

В данном разделе рассмотрим, как определить положение отрезка на координатной плоскости и описывать его вариации.
Когда речь идет о расположении отрезка на плоскости, важно учитывать его положение относительно осей координат. Зная координаты начальной и конечной точки отрезка, можно однозначно определить его положение и ориентацию в пространстве.
Отрезок может находиться полностью ниже оси абсцисс, полностью выше ее или пересекать ее в точке. Также отрезок может располагаться полностью левее оси ординат, полностью правее ее или пересекать ее в точке. Положение относительно осей абсцисс и ординат при расчете положения отрезка очень важно, так как оно позволяет определить, где именно находятся его начальная и конечная точки в пространстве.
Дополнительно ориентация отрезка на плоскости может делить его на две половины, называемые лучами. Если начало отрезка находится левее его конца, то ориентация отрезка будет положительной. В противном случае, ориентация будет отрицательной. Ориентация отрезка также играет важную роль при описании его положения на координатной плоскости.
Итак, рассмотрели основные аспекты положения отрезка на координатной плоскости, включая его положение относительно осей координат и вариации ориентации. В следующих разделах более подробно разберем определение и свойства отрезка.
Декартова система координат и границы пространства
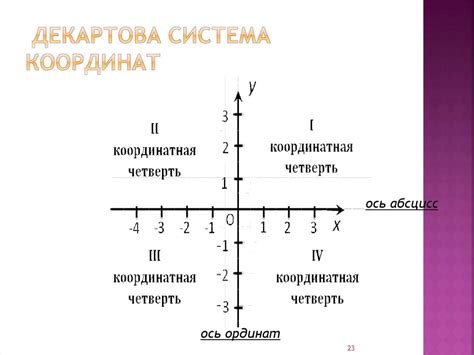
Используя декартову систему координат, мы можем определить границы пространства, а также рассматривать и изучать отрезки, которые представляют собой часть прямой и обладают своими характеристиками и свойствами.
Отрезок в двумерной декартовой системе координат представляет собой часть прямой, заключенной между двумя точками. Он может быть представлен в виде упорядоченной пары чисел, соответствующих координатам начальной и конечной точек отрезка.
Одним из основных свойств отрезка является его длина, которая вычисляется как расстояние между начальной и конечной точками. Кроме того, отрезок может иметь направление - это определяется порядком следования точек. Также отрезок может быть ориентированным, то есть иметь указанное направление, в котором он простирается в пространстве.
Понимание декартовой системы координат и основных свойств отрезка поможет лучше разобраться в их роли и значимости при изучении геометрии и аналитической геометрии. Эти понятия лежат в основе многих математических и физических теорий, а также находят свое применение в различных сферах науки и техники.
Вопрос-ответ

Что такое отрезок?
Отрезок - это часть прямой, ограниченная двумя точками. Отрезок имеет начало и конец, которые являются этими двумя точками.
Как определить начало и конец отрезка?
Начало отрезка - это точка, с которой начинается отрезок. Конец отрезка - это точка, которая является его конечной границей.
Может ли отрезок иметь только начало или только конец?
Нет, отрезок всегда должен иметь и начало, и конец. Отрезок - это участок прямой, ограниченный двумя точками, и по определению он должен иметь обе границы.
Какие свойства отрезков существуют?
Отрезки могут быть равными, параллельными, перпендикулярными, пересекаться или быть непересекающимися. Они также могут быть увеличены или уменьшены в размере путем изменения расстояния между их началом и концом.
Можно ли упорядочить отрезки по их началу и концу?
Да, отрезки могут быть упорядочены по их началу и концу. Это позволяет определить, какой отрезок идет перед другим или за другим на прямой.
Что такое отрезок?
Отрезок - это часть прямой, ограниченная двумя точками. Он имеет начало и конец.



