В процессе изучения математических функций и их поведения на координатной плоскости, становится необходимым находить точки, которые проходят через график функции. Такие точки играют важную роль в анализе и понимании характеристик функции, определении корней или экстремумов и решении различных задач. Для достижения этой цели существует несколько методов и алгоритмов, которые позволяют более точно определить координаты таких точек, используя разнообразные стратегии и инструменты.
Одним из эффективных подходов является использование численных методов, таких как метод деления отрезка пополам, метод Ньютона или метод простых итераций. Эти методы позволяют приближенно находить значения функции в заданной точке, основываясь на её свойствах и особенностях. Используя эти численные методы, мы можем получить более точные результаты и избежать возможных ошибок, которые могут возникнуть при ручном нахождении точек на графике функции.
В то же время, существуют и графические методы, которые позволяют визуально определить точки пересечения графика функции с координатными осями или другими графиками. Например, графики функций могут быть нарисованы на более крупной сетке, чтобы более точно определить их точки пересечения. Кроме того, с использованием специальных программ и компьютерных инструментов, можно создавать 3D-модели и анимации функций, чтобы более наглядно представить и анализировать точки на графике функции.
Каким бы методом ни пользовались, важно помнить о необходимости проверки полученных результатов и оценки их достоверности. Никакой метод или алгоритм не гарантирует абсолютной точности, поэтому необходимо использовать несколько различных методов и сравнивать результаты. Это позволяет увеличить надежность определения точек на графике функции и обеспечить более точные и достоверные результаты в анализе и решении задач, связанных с функциями и их поведением.
Геометрический подход к проверке пролегания точки через кривую функции

Рассмотрим геометрический подход для определения, проходит ли точка через график кривой функции. Вместо использования алгоритмических методов и конкретных проверок, мы можем прибегнуть к применению геометрических принципов и свойств, чтобы определить, лежит ли точка на графике или нет.
Другим способом является использование наклона касательной к графику функции в данной точке. Если касательная кривой функции в данной точке горизонтальна или вертикальна, то точка лежит на графике функции. Путем анализа наклона касательной, основываясь на геометрических принципах, можно определить, проходит ли точка через график функции или нет.
Важно учитывать, что геометрическое решение не обеспечивает точности до бесконечности, но предоставляет визуальное представление и интуитивное понимание прохождения точки через кривую функции. Этот подход особенно полезен в области графического представления функций, при котором требуется быстрая и приближенная оценка прохождения точек, не привязываясь к строгим математическим алгоритмам.
Аналитический подход к проверке прохождения точки графиком функции
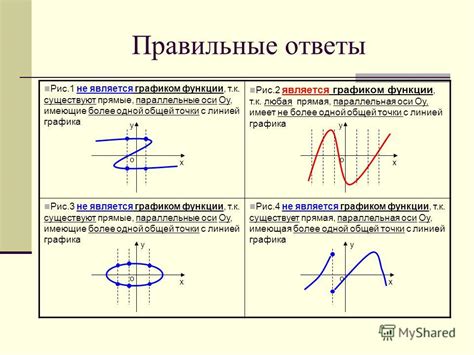
В данном разделе рассмотрим альтернативный способ проверки, основанный на аналитической обработке данных, связанных с прохождением точки графиком функции. Вместо методов и алгоритмов, мы сосредоточимся на основных принципах, ориентируясь на логику и математическую составляющую данного процесса.
Метод подстановки для верификации прохождения определенной точки графиком функции

В данном разделе будет рассмотрен метод подстановки, который позволяет проверить, проходит ли определенная точка через график функции. Этот метод основан на использовании алгебраических преобразований и позволяет установить, удовлетворяет ли точка условиям заданной функции.
Прежде чем приступить к использованию метода подстановки, необходимо определить заданную функцию и интересующую нас точку. После этого мы можем подставить значения координат точки в уравнение функции и выполнить вычисления. Если после подстановки полученное утверждение равно, то точка принадлежит графику функции; в противном случае, точка не проходит через график функции.
Пример использования метода подстановки:
| Функция: | y = 2x + 3 |
|---|---|
| Точка: | (2, 7) |
Для проверки прохождения точки через график функции, подставим значения координат точки в уравнение функции:
| Уравнение: | y = 2x + 3 |
|---|---|
| Значения: | x = 2, y = 7 |
| Подстановка: | 7 = 2 * 2 + 3 |
| Вычисление: | 7 = 4 + 3 |
| Утверждение: | 7 = 7 |
Уравнение после подстановки верно, следовательно, точка (2, 7) проходит через график функции y = 2x + 3.
Метод подстановки является простым и надежным способом проверки прохождения точки через график функции. Он может применяться для различных типов функций и помогает установить соответствие между заданной точкой и уравнением функции. Важно помнить, что данная методика требует аккуратности при выполнении алгебраических преобразований для получения верного утверждения.
Использование производных для проверки пролегания точки по кривой графика функции
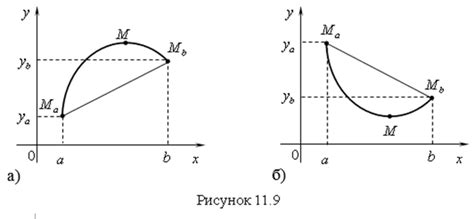
В данном разделе мы рассмотрим метод, основанный на использовании производной функции для определения того, пролегает ли точка по кривой графика данной функции или нет.
Производная функции является одним из основных инструментов в дифференциальном исчислении и позволяет нам анализировать изменение функции в различных точках ее области определения.
Идея метода заключается в том, что если точка лежит на графике функции, то касательная к графику в этой точке будет горизонтальной. Это означает, что производная функции в данной точке равна нулю.
Следовательно, для проверки пролегания точки по кривой графика функции, мы можем рассчитать производную функции и проверить, равна ли она нулю в данной точке. Если производная равна нулю, то точка лежит на графике функции, а если производная отлична от нуля, то точка не пролегает по кривой графика.
Таким образом, использование производных позволяет нам с уверенностью определить, проходит ли точка по графику функции или нет, что является важным инструментом при анализе и исследовании функций.
Проверка прохождения точки графиком функции с помощью уравнений
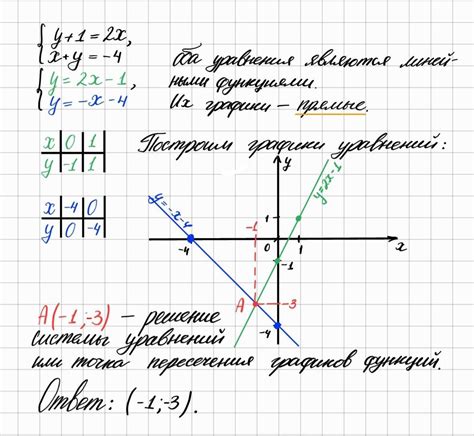
В этом разделе мы рассмотрим подходы к проверке прохождения точек графиком функции, используя уравнения. При анализе и проверке точек на принадлежность графику функции, можно использовать уравнения, которые описывают эту функцию.
Одним из методов является подстановка координат точки в уравнение функции и проверка выполнения равенства. Для этого необходимо знать уравнение функции и координаты точки. Если после подстановки результат будет совпадать по обеим сторонам, то точка принадлежит графику функции.
Другим методом является вычисление функции в точке и сравнение полученного значения с координатой по оси y. Если они совпадают, то точка лежит на графике функции. Этот метод подходит для таких функций, у которых непосредственно задано выражение, например, многочлены или тригонометрические функции.
Также существуют другие подходы, основанные на геометрических свойствах графика функции. Например, можно использовать максимальное и минимальное значение функции для определения интервала, в котором должны находиться координаты точек, лежащих на графике. Затем проверяются координаты точки на соответствие этому интервалу.
Важно учитывать особенности и ограничения каждого метода при выборе способа проверки прохождения точки графиком функции. Это поможет достичь более точного результата и предотвратить возможные ошибки в анализе данных.
Использование метода интерполяции для определения прохождения точки графиком функции
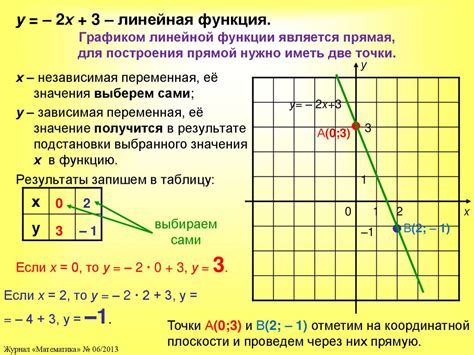
В данном разделе рассматривается метод интерполяции, который может быть использован для проверки прохождения точки через график функции. Этот метод позволяет установить, находится ли заданная точка на графике функции, используя данные о значениях функции в соседних точках. С помощью интерполяции можно определить местонахождение точки на графике и с высокой точностью установить, проходит ли она через функцию или находится за её пределами.
Интерполяция – это метод, позволяющий оценивать значения между известными точками посредством анализа их положения относительно одной или нескольких функций. В данном контексте интерполяция применяется для определения координат точки на графике функции по значениям функции в близлежащих точках.
Метод интерполяции позволяет улучшить точность определения прохождения точки графиком функции, особенно в случаях, когда имеется ограниченное количество данных о функции или когда у функции нет аналитического выражения. Использование интерполяции помогает установить наличие или отсутствие точки на графике функции с достаточной достоверностью, что является важным в задачах анализа данных и построения моделей на основе экспериментальных наблюдений.
Метод линейной аппроксимации: определение прохождения точки через график функции

Иногда нам требуется проверить, проходит ли точка через график функции, но у нас нет точного математического описания этой функции. Для таких случаев применяется метод линейной аппроксимации, который позволяет приблизительно определить, проходит ли точка через график функции.
Основная идея метода линейной аппроксимации заключается в том, чтобы использовать линейную функцию, которая наилучшим образом приближает график исследуемой функции вблизи данной точки. Путем нахождения уравнения этой линейной функции и подстановки значений координат точки мы можем определить, находится ли данная точка на графике функции или нет.
Для применения метода линейной аппроксимации необходимо взять две близкие точки на графике функции, а затем построить прямую линию, проходящую через эти две точки. Затем мы можем использовать это уравнение прямой линии для проверки, проходит ли данная точка через график функции.
Однако необходимо понимать, что метод линейной аппроксимации не дает точного ответа на вопрос о прохождении точки через график функции, так как он основан на приближении. В зависимости от выбранных точек на графике и особенностей функции, метод может давать ложноположительные или ложноотрицательные результаты. Поэтому следует использовать этот метод с осторожностью и всегда учитывать его ограничения.
Графическое представление для определения прохождения точки на графике функции

В данном разделе мы рассмотрим способы проверки, с помощью графического представления, прохождения точки на графике функции без применения сложных методов и алгоритмов. Мы представим некоторые визуальные приемы и интуитивные подходы, которые помогут нам определить, пересекает ли график функции заданную точку.
Для начала, необходимо представить график функции на координатной плоскости. При анализе графика можно использовать метод графического образа функции, который позволяет нам визуально представить изменения значений функции в зависимости от аргумента. С помощью графического представления мы можем оценить общий характер поведения функции и выявить ее особенности.
Для проверки прохождения точки на графике функции, можно использовать следующие подходы:
- Проверка положения точки относительно графика функции: если точка находится выше графика функции, то это может указывать на то, что функция не проходит через эту точку. Аналогично, если точка находится ниже графика функции, то есть большая вероятность, что функция проходит через эту точку.
- Анализ направления кривизны графика: если сегмент графика функции в окрестности точки выпуклый вверх, то это может говорить о том, что функция не проходит через эту точку. В случае, если сегмент графика функции выпуклый вниз, то есть вероятность, что функция проходит через эту точку.
- Оценка динамики изменения графика функции: если график функции в окрестности точки меняется достаточно резко, то это может указывать на непрохождение функции через эту точку. Плавное изменение графика в окрестности точки, наоборот, может говорить о прохождении функции через эту точку.
С помощью данных простых графических приемов мы можем визуально оценить, проходит ли функция через заданную точку или нет. Конечно, результаты такой проверки не являются абсолютно точными, однако они могут дать нам первоначальное представление о степени прохождения точки графиком функции.
Компьютерные подходы к определению принадлежности точки графику функции
Узнаем, как с помощью компьютерных методов можно определить, лежит ли точка на графике функции. В этом разделе мы рассмотрим различные подходы, которые позволяют нам эффективно проверить принадлежность точки к графику функции. Вместо простой проверки геометрически, мы применим вычислительные алгоритмы и методы, чтобы дать точные ответы.
Геометрические методы позволяют нам определить, лежит ли точка на графике функции, используя знания о форме функции и ее геометрии. График представляется в виде математического объекта, и мы можем проверить, находится ли точка внутри или снаружи этого объекта. Однако этот подход имеет свои ограничения; он может быть сложным для функций с нетривиальной формой и требовать точного знания графика.
Аналитические методы основаны на математическом анализе графика функции. Мы используем знания о поведении функции для анализа точки и проверяем, соответствует ли она свойствам графика функции. Например, можно использовать производные функции, чтобы определить поведение функции вблизи точки, и сравнить ее с координатами точки. Этот подход требует знания математических методов и может быть затратным с точки зрения ресурсов вычислительной техники.
Численные методы позволяют нам приближенно вычислить значение функции в точке и сравнить его с координатами точки. Мы используем алгоритмы численного анализа и численной оптимизации, чтобы получить приближенное решение. Этот подход удобен тем, что он не требует точного знания графика и является более общим.
В зависимости от конкретной задачи и доступных ресурсов, можно выбрать подходящий метод для проверки принадлежности точки графику функции. Компьютерные методы существенно упрощают эту задачу, позволяя быстро и точно определить, лежит ли точка на графике функции, даже для сложных функций и точек с большими координатами.
Вопрос-ответ

Какие методы и алгоритмы существуют для проверки прохождения точки графиком функции?
Существует несколько методов и алгоритмов для проверки прохождения точки графиком функции. Один из них - метод подстановки, когда вместо переменных подставляются значения координат точки и проверяют, выполняется ли равенство. Еще один метод - алгоритм построения графика функции, в котором необходимо отметить заданную точку и оценить, находится ли она на графике или вне его. Также существуют методы векторного анализа, где используются определенные свойства векторов и их направления для проверки прохождения точки графиком функции.
Каким образом работает метод подстановки для проверки прохождения точки графиком функции?
Метод подстановки для проверки прохождения точки графиком функции заключается в подставлении значений координат точки вместо переменных функции и проверке выполнения равенства. Если после подстановки равенство выполняется, то точка проходит график функции, если нет - то не проходит. Например, для функции y = x^2 - 3x + 2, чтобы проверить, проходит ли точка (2, 0) график функции, необходимо подставить x = 2 и y = 0 в уравнение функции и убедиться, что получится верное равенство 0 = 0.
Что представляет собой алгоритм построения графика функции для проверки прохождения точки?
Алгоритм построения графика функции для проверки прохождения точки заключается в построении самого графика функции и отметке заданной точки на этом графике. После этого необходимо оценить, находится ли точка на графике или вне его. Если точка находится на графике, то она проходит его, если нет - то не проходит. Например, для функции y = sin(x), чтобы проверить, проходит ли точка (π/2, 1) график функции, необходимо построить график функции с помощью требуемого диапазона значений x и отметить точку (π/2, 1) на этом графике.
Каким образом методы векторного анализа могут быть использованы для проверки прохождения точки графиком функции?
Методы векторного анализа используют определенные свойства векторов и их направления для проверки прохождения точки графиком функции. Один из таких методов - использование касательных векторов к графику функции в данной точке. Если вектор, проведенный из данной точки и параллельный касательной вектору, выходит из графика, то точка не проходит график функции. Если же вектор остается внутри графика, то точка проходит. Этот метод основан на свойствах кривизны и наклона графика функции в данной точке.