Добро пожаловать в увлекательный мир математики, где мы погрузимся в глубины исследования свойств функции y xn! Если вы когда-либо задавались вопросом о том, как эта функция работает и какие принципы ей присущи, то наша статья специально для вас.
Функция y xn – это не просто серия букв и цифр, скрытых под огромным числом возможностей. Она представляет собой мощный инструмент, который используется в различных областях науки и промышленности. Она может помочь нам понять изменение величин, производство математических моделей и даже решение сложных задач.
В этой статье мы рассмотрим различные аспекты функции y xn: ее происхождение, способы решения и важность в современном мире. Мы более внимательно рассмотрим применение этой функции в физике, экономике и других научных областях. Глубоко погрузившись в изучение свойств функции y xn, мы узнаем, как эта функция может быть использована для анализа и предсказания различных явлений и является неотъемлемой частью современной науки.
Сущность и уникальность функции умножения на переменную степень

- Гибкость и предсказуемость процесса умножения на переменную степень.
- Эффективность и универсальность применения функции y xn.
- Возможность использования функции y xn в моделировании сложных процессов.
- Преимущества функции y xn перед другими математическими операциями.
- Примеры применения функции y xn в различных областях науки и практики.
Понимание сущности и особенностей функции умножения на переменную степень позволит использовать ее с высокой эффективностью и точностью при решении разнообразных задач, а также совершенствовать существующие методы анализа и моделирования.
Определение и структура функции y xn

Функция y xn – это математическое выражение, которое связывает две переменные: x и y. Она представляет собой зависимость значения y от значения x, причем исходное число x (в степени n) является основанием этой зависимости. Функция y xn может иметь различные степени, представленные как целые, положительные или отрицательные числа.
Структура функции y xn обычно представляется в виде алгебраического выражения, включающего переменные x и y, а также степень n. Такая формула позволяет определить соответствующий график зависимости значений y от значений x.
- Функция y xn может быть представлена как моном – алгебраическое выражение, содержащее только одно слагаемое. Примером такой функции может быть y = x^2.
- Другим вариантом функции y xn является полином – алгебраическое выражение, содержащее несколько слагаемых. Примером такой функции может быть y = 2x^2 - 3x + 1.
- Функция y xn может иметь различные свойства, такие как симметричность относительно оси ординат или асимптотичность в некоторых точках.
Использование функции y xn позволяет анализировать зависимости между переменными и строить соответствующие графики, что находит широкое применение в различных областях науки и техники.
Особенности функции y xn и ее графика
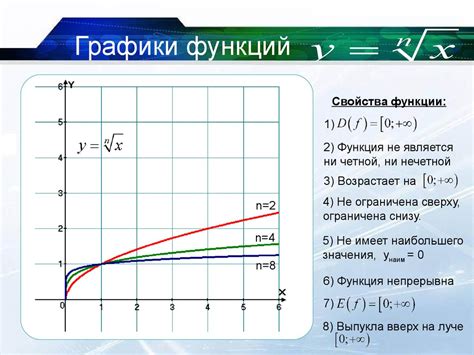
Исследование функции y xn и построение ее графика позволяет нам углубить наши знания о данной функции и раскрыть ее особенности, которые существенно влияют на ее поведение и свойства.
Когда мы изучаем функцию y xn, мы исследуем ее производную и интеграл, устанавливаем условия ее определения и трансформации, анализируем ее поведение при изменении значения показателя степени и определяем ее особенности на основе полученных результатов.
Одной из важных особенностей функции y xn является возможность различения ее типа графика в зависимости от значения показателя степени. Например, при нечетном значении показателя степени график функции y xn является симметричным относительно оси y, а при четном - симметричным относительно обоих осей.
Кроме того, функция y xn обладает свойством монотонности в зависимости от значения показателя степени: при положительном значении показателя график функции возрастает, а при отрицательном - убывает.
Необходимо также важное свойство интервалов определения функции y xn, которое определяет границы значения аргумента, на которых функция действует и имеет смысл. Изучение этих интервалов позволяет нам более точно анализировать поведение функции и выявить ее особые точки, такие как точки перегиба и экстремумы.
Исследование особенностей функции y xn и ее графика помогает нам полностью понять ее свойства, определить ее тип и поведение, а также использовать ее в различных математических задачах и приложениях.
Примеры функции y xn в реальной жизни
Один из применений функции y xn может быть в исследовании динамики роста некоторых организмов, например, растений. В этом случае, степень n может определять, например, высоту растения, а результатом работы функции будет описание зависимости между возрастом растения и его размером. Таким образом, функция y xn помогает нам понять, как величина изменяется при изменении возведения в степень.
Еще одним примером использования функции y xn является моделирование экономических процессов. Например, при исследовании зависимости между объемом продаж и ценой товара, мы можем использовать функцию y xn для определения влияния изменения цены на объем продаж. В данном случае, степень n может определять эластичность спроса, а результатом работы функции будет описание того, как изменение цены влияет на количество проданных товаров.
Таким образом, примеры функции y xn в реальной жизни демонстрируют ее эффективность при моделировании различных явлений и исследования их зависимостей. Она позволяет нам рассматривать значения какиx-либо показателей в зависимости от их возведения в степень n, что открывает новые возможности для анализа данных и понимания окружающего мира.
Вопрос-ответ

Какие свойства имеет функция y = xn?
Функция y = xn является степенной функцией и имеет несколько важных свойств. Во-первых, она является четной функцией, если показатель степени n является четным числом, и нечетной функцией, если n - нечетное число. Во-вторых, она всегда принимает только положительные значения при положительных значениях x, независимо от знака показателя степени. Третьим свойством является то, что функция y = xn имеет горизонтальную асимптоту при n > 0, которая проходит через точку (0,0). И, наконец, функция y = xn имеет так называемую "сигнатуру" в зависимости от значения показателя степени - при нечетном значении n функция имеет форму буквы "n" с выпуклостью вверх или вниз в зависимости от знака n, а при четном значении n функция имеет форму буквы "u" с выпуклостью вверх или вниз в зависимости от знака n.
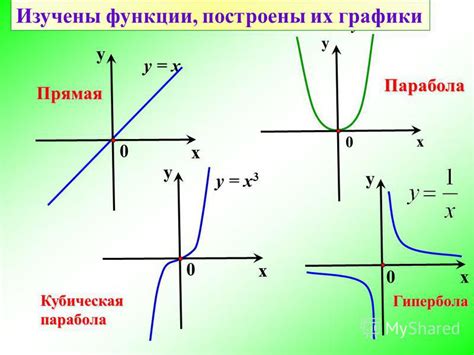
Какая графическая форма у функции y = xn при различных значениях показателя степени?
Функция y = xn имеет различную графическую форму в зависимости от значения показателя степени n. При нечетном значении n график функции имеет форму буквы "n" с выпуклостью вверх или вниз в зависимости от знака n. Так, при n = 1 график функции y = x образует прямую линию под углом 45 градусов к оси абсцисс. При n = 3 график функции будет выглядеть как парабола с вершиной в начале координат. При n = 5 график будет напоминать форму "с" с выпуклостью вверх или вниз. При четном значении n форма графика будет угловатой и напоминает букву "u" с выпуклостью вверх или вниз.
Какую роль играет показатель степени в функции y = xn?
Показатель степени n играет решающую роль в функции y = xn, так как определяет ее свойства и графическую форму. Если n является четным числом, то функция будет иметь графическую форму буквы "u" с выпуклостью вверх или вниз, в зависимости от знака n. Если n является нечетным числом, то график функции будет иметь форму буквы "n" с выпуклостью вверх или вниз. Также значение показателя степени влияет на четность функции - при нечетном значении n функция является нечетной, а при четном значении - четной. Показатель степени также определяет наличие горизонтальной асимптоты (при n > 0) и положительное значение функции при положительных значениях x.