Проникнуть в мир параллельности прямых в различных плоскостях - значит погрузиться внутрь самого фундамента, на котором строится наше понимание пространства. Как зрительно уловить параллельность движений, которая слишком часто становится неподатливой для нашего взора? Разбор этой возможности позволит нам разгадать множество тайн геометрии, приоткрыв при этом истинную природу взаимосвязи математики и реального мира.
Стремительные движения, неукротимая энергия, которая возникает при взаимодействии параллельных прямых в различных плоскостях, оказываются заложенными в самой сути пространства. В значимости таких радикальных конструкций, как строящийся нами мир, находится своеобразная гармония. Именно параллельность выступает в данной ситуации в качестве важнейшей шкалы, измеряющей пространственно-временные взаимодействия.
Геометрия, ставшая предметом нашего рассмотрения, лишает нас возможности остаться в рамках поверхностного понимания мира. Параллельность прямых, пересекающихся во множестве плоскостей, вовлекает в свою систему того, кто стремится разобраться в ее тайнах. Анализируя их взаимодействие, мы открываем новые грани сознания и позволяем себе заглянуть за пределы привычных ощущений и впечатлений.
Основные концепции и свойства параллельных линий

В данном разделе мы рассмотрим основные концепции и свойства, связанные с параллельными линиями. Без параллельности в геометрии было бы невозможно описать множество физических и математических явлений, связанных с пространством и формами.
Первое важное понятие, которое мы рассмотрим, - это равнобедренность. Равнобедренные линии имеют одинаковые углы с другими прямыми и плоскостями в пространстве, что приводит к их параллельности. Они сохраняют свои пропорции и форму независимо от положения в пространстве. Это свойство позволяет использовать равнобедренные линии в различных областях науки и техники, таких как архитектура и инженерия.
Другим важным свойством параллельных линий является параллельный перенос. Параллельный перенос позволяет перемещать линии или фигуры в пространстве без изменения их формы и размеров. Это особенно полезно при проектировании и моделировании, где необходимо создать точные копии объектов в разных масштабах и положениях.
Также, важно отметить, что параллельные линии имеют важные геометрические свойства. Например, они никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга. Это свойство позволяет использовать параллельные линии в измерительных приборах и устройствах для обеспечения точности и надежности измерений.
Устройство пространства: происхождение разнообразия плоскостей

Изучение структуры пространства представляет собой сложную задачу, особенно когда речь идет о возникновении различных плоскостей. Рассмотрим процесс формирования разных уровней, которые упорядочивают пространство и создают основу для существования параллельных прямых в нем.
Одной из основополагающих идей является представление пространства как расслоенной среды. В этом случае мы можем рассматривать каждый слой пространства как отдельную плоскость, имеющую свои характеристики и особенности. Такие плоскости могут быть расположены параллельно друг другу или иметь определенные углы наклона.
Возникновение разнообразных плоскостей обусловлено многими факторами, включая взаимодействие материалов и энергии в пространстве, а также гравитационные, электромагнитные и другие типы полей. В процессе формирования плоскостей возникают различные силы и противодействия, которые организуют зоны отделения и сегментацию пространства.
Интересно отметить, что разнообразные плоскости могут существовать на разных масштабных уровнях. Например, в микромире мы сталкиваемся с плоскостями атомов и молекул, а в макромире - с плоскостями планет и звезд. Такое разбиение пространства на различные плоскости позволяет нам лучше понять организацию мира вокруг нас и разрабатывать более точные модели его функционирования.
Параллельность линий в одной плоскости: определение и методы
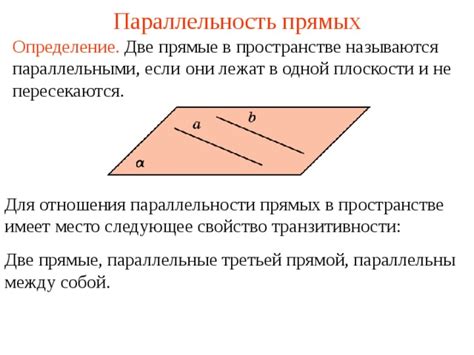
В данном разделе рассматривается явление параллельности прямых линий, которые находятся в одной плоскости. Здесь будут представлены основные уравнения и методы определения параллельности, а также обсуждается их применение в различных областях науки и техники.
Уравнения параллельных линий в одной плоскости
Одним из основных способов определения параллельности прямых в одной плоскости является анализ их уравнений. Важным критерием является то, что в уравнениях параллельных линий определены коэффициенты, которые пропорциональны друг другу или имеют одинаковый знак.
Методы определения параллельности линий
Определение параллельности линий в одной плоскости может быть осуществлено различными методами. Один из них - метод сравнения коэффициентов наклона линий. Если у двух линий значения их коэффициентов наклона совпадают, то они будут параллельны. Другой метод - использование геометрических конструкций, таких как построение параллельных линий через заданную точку и использование инструментов геометрии для проверки условий параллельности.
Изучение параллельности прямых линий в одной плоскости является важной задачей в геометрии и аналитической геометрии. Это позволяет анализировать и описывать множество физических явлений, структур и объектов в пространстве. Строгое определение и корректное определение параллельности линий в одной плоскости позволяет разрабатывать более точные модели и расчетные методики в различных научных и технических областях.
Движение исходных линий в результате трансплантации плоскостей
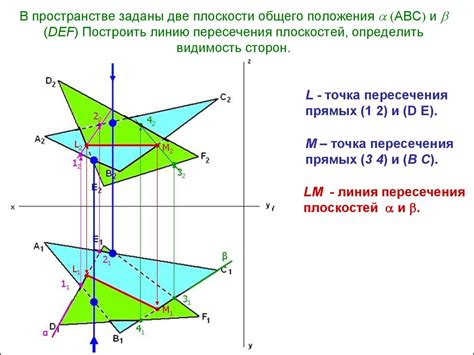
При проведении трансплантации плоскости, линии, которые изначально были параллельными друг другу, могут приобретать новые положения или оставаться параллельными, но перемещаться на различное расстояние. Движение их исходных точек определяется разной ориентацией исходной плоскости в новой системе координат.
Трансплантация плоскостей является важным инструментом для анализа пространственных геометрических структур и позволяет исследовать взаимодействие линий и плоскостей в различных перспективах. Результаты данного исследования могут иметь практическое применение в таких областях как архитектура, графический дизайн и компьютерная графика.
Изучение движения исходных линий при трансплантации плоскостей позволяет получить новые визуальные эффекты и перспективы, а также обнаружить взаимосвязи и зависимости между прямыми, которые не всегда возможно заметить, работая только с одной плоскостью.
Взаимное расположение соответствующих прямых в пространстве и плоскости
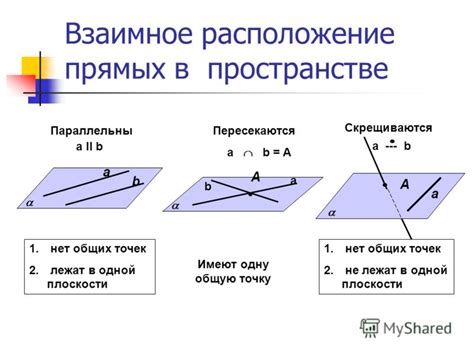
В данном разделе мы рассмотрим важное свойство взаимного расположения параллельных прямых в разнообразных пространствах и плоскостях. Изучение данного вопроса позволит нам более глубоко осознать взаимосвязь и взаимное влияние прямых, находящихся в разных плоскостях, а также понять, как это свойство может быть использовано в различных практических ситуациях.
Взаимное расположение параллельных прямых часто является неотъемлемой частью решения геометрических задач и применяется в различных областях науки и техники. Это свойство может быть применено при построении и проектировании архитектурных конструкций, разработке оптических систем, планировании дорожных и железнодорожных трасс, а также в компьютерной графике и промышленном дизайне.
В данном разделе будут рассмотрены основные характеристики и признаки взаимного расположения параллельных прямых на разных плоскостях. Будут представлены различные методы определения, классификации и графического изображения параллельности прямых, а также рассмотрены основные геометрические свойства этого взаимного расположения. Кроме того, будет обсуждена возможность применения данного свойства в практических задачах и областях науки.
Взаимное расположение прямых | Возможные области применения |
Параллельность прямых в разных плоскостях | Архитектура, инженерия, компьютерная графика |
Точечная, линейная и плоская параллельность | Оптические системы, дорожное строительство |
Методы определения и классификации | Железнодорожное дело, промышленный дизайн |
Ограничения на параллельность прямых в различных плоскостях
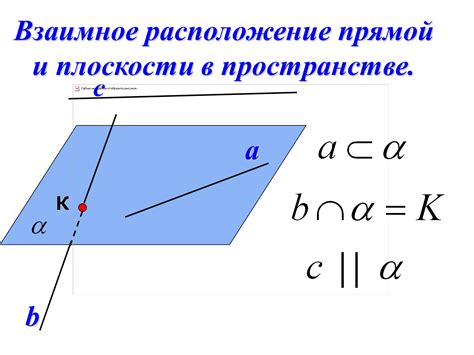
Существуют определенные ситуации, при которых невозможно достичь параллельности между прямыми, находящимися в разных плоскостях. В таких случаях возникают определенные ограничения, препятствующие равномерному расположению данных прямых. Изучение данных ограничений предоставляет возможность лучше понять и описать геометрические взаимосвязи между прямыми в пространстве.
- Ситуация, когда прямые находятся в плоскостях, параллельных, но неидентичных друг другу, требует отдельного рассмотрения. Несоответствие между определенными характеристиками плоскостей приводит к тому, что параллельность прямых становится недостижимой. В таких случаях требуется детальный анализ различий и изучение возможных пространственных ограничений, препятствующих параллельному расположению прямых.
- Другая ситуация возникает, когда прямые находятся в плоскостях, пересекающихся под определенным углом. В таких случаях параллельность прямых также оказывается недостижимой. Это связано с особенностями геометрической природы пересекающихся плоскостей, которые не обеспечивают совпадение направлений прямых. Исследование данных ситуаций требует учета углового взаимодействия, а также анализа основных аспектов, влияющих на ориентацию прямых в пространстве.
- Также существуют случаи, когда прямые находятся в плоскостях, которые пересекаются под углом 90 градусов. В данных ситуациях параллельность также оказывается невозможной. Объяснение этому факту можно найти в особенностях пересечения плоскостей под правым углом и изучении их структурных свойств.
При обнаружении данных ограничений на параллельность прямых в разных плоскостях важно применить соответствующие методы и инструменты для анализа геометрических характеристик и организовать систематизацию знаний, которая поможет более полно и точно описать эти ограничения.
Практическое использование концепции параллельности линий в различных плоскостях

В данном разделе мы рассмотрим практические применения концепции движения вдоль параллельных линий в разных пространствах. Это важное понятие имеет широкое применение в различных областях, таких как инженерия, архитектура, геодезия, транспортное планирование и т. д.
Например, в инженерии параллельные линии используются для создания эффективных систем передачи энергии и данных. Провода и кабели располагаются параллельно, чтобы минимизировать помехи и потери сигнала. Кроме того, в архитектуре параллельные линии могут использоваться для создания эстетически приятных и симметричных фасадов зданий.
В геодезии параллельные линии применяются для определения географической широты и долготы. На основе параллельности линий строятся системы координат, которые позволяют точно определить местоположение объектов на земле.
Кроме того, в транспортном планировании параллельные линии используются для проектирования эффективных систем дорог. Параллельные улицы и дороги позволяют обеспечить плавный поток движения транспорта без перекрестков и пробок.
Таким образом, понимание и использование концепции параллельности линий в различных плоскостях является важным инструментом во многих областях, от инженерии и архитектуры до геодезии и транспортного планирования.
Вопрос-ответ

Как определить, будут ли прямые параллельными в разных плоскостях?
Для определения параллельности прямых в разных плоскостях необходимо проверить, являются ли эти плоскости параллельными. Если плоскости параллельны и одна прямая лежит в одной плоскости, а вторая - в другой, то эти прямые будут параллельными в разных плоскостях.
Могут ли прямые, пересекающиеся в одной плоскости, быть параллельными в других плоскостях?
Нет, прямые, которые пересекаются в одной плоскости, никогда не будут параллельными в других плоскостях. Параллельные прямые никогда не пересекаются, поэтому если они пересекаются в одной плоскости, то они уже не могут быть параллельными в других плоскостях.
Каким образом можно показать параллельность прямых в разных плоскостях графически?
Для графического отображения параллельности прямых в разных плоскостях можно использовать координатные оси. Построив две прямые, которые никогда не пересекаются, и расположив их в разных плоскостях, можно показать, что они параллельны друг другу в разных плоскостях.
Какую информацию о прямых нужно знать для определения их параллельности в разных плоскостях?
Для определения параллельности прямых в разных плоскостях необходимо знать их уравнения и расположение относительно друг друга. Также важно знать, являются ли соответствующие плоскости параллельными.
Можно ли сказать, что все прямые, параллельные в одной плоскости, будут параллельными в других плоскостях?
Нет, нельзя сказать, что все прямые, параллельные в одной плоскости, будут параллельными в других плоскостях. Параллельные прямые остаются параллельными только в рамках своих плоскостей, и необходимо дополнительное исследование, чтобы определить, будут ли они параллельными в других плоскостях.



