Глубоко в корнях науки о геометрии, сокровенные принципы кристаллизуются в понимании связи между элементами фигуры, из которых мы строим наш мир. Одной из главных характеристик многоугольника является сумма длин его сторон. Эта фундаментальная величина хранит в себе немало интересных особенностей и закономерностей, которые могут зажечь воображение даже наиболее скептически настроенного исследователя.
В эстетических формах геометрии лежит магия чисел, взаимодействующих друг с другом и создающих гармонию. Сумма длин сторон многоугольника - это образец прекрасной гармонии в геометрическом мире. Отталкиваясь от этой величины, мы можем узнать о глубине фигуры, о ее структуре и энергетике. Суть закономерностей является ключом к пониманию и разгадке тайны многоугольников.
Заложенные в основу геометрии принципы и своего рода законы, устанавливают костяк фигуры. Исходя из этих понятий, у нас есть возможность не только рассчитать сумму длин сторон многоугольника, но и предсказать некоторые его особенности без использования сложных формул и уравнений. Все это позволяет нам приблизиться к логической структуре и суть многоугольника, показав нам его характер и, возможно, даже позволяя нам заглянуть в его душу.
По определению: что представляет собой сумма отрезков, образующих фигуру?

Сумма длин отрезков, составляющих многоугольник, указывает на общую длину его периметра, который представляет собой замкнутую линию, охватывающую внутреннюю часть фигуры. Поэтому данная характеристика важна для определения размерности и формы многоугольника – она позволяет оценить степень охвата его внешнего пространства.
Сумма длин сторон может быть варьирующейся величиной, которая зависит от состава и размещения отрезков. Разнообразные комбинации сторон многоугольника могут создавать различные формы и размеры: от простых треугольников и прямоугольников до более сложных пятиугольников и шестиугольников. Каждый многоугольник имеет свою характеристику периметра, которая отражает его конкретную сумму длин сторон.
Подводя итоги, сумма длин сторон многоугольника – это совокупная длина всех его сторон, определяющая размеры и форму фигуры. Это важная характеристика, которая позволяет нам визуально представить многоугольник и оценить его периметр, а также использовать эту информацию в решении различных математических задач и расчетах.
Почему важно знать сумму всех сторон фигуры в геометрии?

- Определение периметра: знание суммы сторон позволяет нам определить периметр любой геометрической фигуры. Измерение периметра является одним из основных способов классифицировать различные фигуры и сравнивать их размеры.
- Планирование и измерение: знание суммы сторон фигуры помогает в планировании различных проектов и измерении их размеров. Будь то проектирование здания, размещение мебели или строительство дороги, знание суммы длин сторон позволяет нам точно рассчитать необходимые материалы.
Таким образом, знание суммы всех сторон фигуры позволяет нам не только более полно и глубоко понять ее структуру и свойства, но и применять это знание на практике в различных сферах деятельности.
Упрощение расчетов в геометрии

В этом разделе мы рассмотрим методы упрощения вычислений в геометрии, которые позволят нам более эффективно работать с геометрическими объектами.
- Использование эффективных алгоритмов для нахождения длин сторон и других параметров фигур, позволяющих сократить количество вычислений и приближенно определить значения.
- Применение геометрических свойств и теорем для упрощения расчетов. Например, применение теоремы Пифагора для нахождения длины диагонали прямоугольника или использование формулы для нахождения периметра круга по радиусу.
- Использование стандартных формул и таблиц для упрощения вычислений. Например, использование таблицы тригонометрических функций для расчета углов в треугольниках.
- Применение геометрических преобразований для упрощения вычислений. Например, сведение сложных фигур к простым геометрическим объектам с помощью подобия или обратного преобразования.
Упрощение вычислений в геометрии позволяет нам экономить время и ресурсы при решении задач, а также дает возможность быстрее и точнее проверять правильность полученных результатов. В следующих разделах мы рассмотрим конкретные примеры применения этих методов и алгоритмов в различных геометрических задачах.
Решение задач на создание геометрических фигур
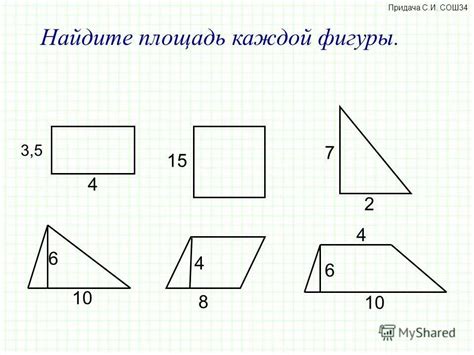
Этот раздел статьи предназначен для тех, кто интересуется решением задач связанных с построением различных многоугольников. Здесь вы найдете подробные объяснения и инструкции, которые помогут вам научиться строить многоугольники по заданным условиям.
Многоугольники - это плоские геометрические фигуры, состоящие из отрезков, называемых сторонами. В зависимости от количества сторон, они могут быть треугольниками, четырехугольниками, пятиугольниками и так далее. Ваша задача заключается в описании и строительстве многоугольников с определенными характеристиками, такими как углы, длины сторон, координаты вершин и другие.
В процессе решения задач на построение многоугольников важно использовать знания из геометрии, такие как теоремы о треугольниках, формулы для вычисления длины сторон и нахождения углов. Также пригодятся навыки работы с координатами и использование графических инструментов для точного построения многоугольников.
В этом разделе мы представим вам различные примеры задач на создание многоугольников и шаги, необходимые для их решения. Мы разберем основные правила и стратегии, которые помогут вам эффективно решать задачи на построение многоугольников. Вы узнаете, как определить количество сторон многоугольника, какие условия нужно использовать для построения многоугольников с определенными свойствами, и как проверить правильность построенных фигур.
В конце статьи, вы будете смело использовать полученные знания и навыки для решения сложных задач на построение многоугольников в своих учебных и практических заданиях. Начните прямо сейчас и расширьте свой арсенал геометрических инструментов!
Как определить общую длину границ простого многоугольника?

Для начала, необходимо отметить, что простой многоугольник - это многоугольник, все стороны которого не пересекаются и никакие вершины не находятся на одной прямой. Понимая это, мы можем упростить процесс вычисления длины границы до последовательного сложения всех сторон.
Важно отметить, что каждая сторона многоугольника может быть определена с использованием координат его вершин. Например, для треугольника можно использовать теорему Пифагора для вычисления длины, зная координаты всех трех вершин. Аналогично, для более сложных многоугольников можно применить геометрические алгоритмы и формулы, используя координаты вершин и длину каждой стороны.
Таким образом, вычисление общей длины границы простого многоугольника требует знания координат его вершин и применение соответствующих геометрических алгоритмов. Это позволяет точно определить длину границы и использовать эту информацию для решения различных задач в области геометрии и аналитической геометрии.
Формула периметра для треугольника
В данном разделе рассмотрим способы вычисления суммы длин сторон для треугольника, одной из самых простых и фундаментальных геометрических фигур. Зная формулу для треугольника, можно более глубоко понять его свойства и применение в различных областях.
Треугольник - это плоская геометрическая фигура, состоящая из трех сторон и трех углов. Он является основным элементом в геометрии и находит широкое применение в различных науках и практических задачах. В данном разделе мы рассмотрим как вычислить сумму длин сторон треугольника, используя простую и удобную формулу.
| Треугольник | Формула |
|---|---|
| Равносторонний треугольник | Три стороны треугольника равны между собой |
| Равнобедренный треугольник | Сумма длин двух сторон равна длине третьей стороны |
| Прямоугольный треугольник | Сумма квадратов катетов равна квадрату гипотенузы |
| Произвольный треугольник | Сумма длин любых двух сторон больше длины третьей стороны |
Используя указанные формулы, можно вычислить сумму длин сторон для различных типов треугольников. Это поможет нам лучше понять их свойства, а также использовать данную информацию в различных математических задачах и реальных ситуациях.
Конвексный многоугольник: расчет суммы длин его периметра
В данном разделе мы рассмотрим формулу, позволяющую вычислить сумму длин сторон конвексного многоугольника, основываясь на его геометрии и свойствах. Благодаря данной формуле можно определить общую длину периметра многоугольника, используя синонимы для терминов "сумма", "длины", "сторон" и "многоугольника".
Принцип работы формулы основывается на следующих факторах:
- Использование понятия "периметр" вместо "суммы длин сторон" позволяет охватить все грани многоугольника в одном термине.
- Конвексный многоугольник - это многоугольник, у которого все его углы меньше 180 градусов. Это свойство обеспечивает единственность рассматриваемого многоугольника.
- Уникальность многоугольника определяется его геометрией и структурой.
- Для вычисления периметра необходимо учесть длину каждой стороны многоугольника, которая зависит от его формы и размеров.
Понимание и применение формулы для расчета периметра конвексного многоугольника является важным аспектом в геометрии. Знание данной формулы позволяет точно определить длину грани любого конвексного многоугольника, расширяя наши возможности в решении геометрических задач.
Как определить общую длину многопланового полигона?

В данном разделе мы рассмотрим методы и алгоритмы определения суммарной длины составной геометрической фигуры с различными гранями и углами. Мы исследуем способы вычисления общей длины ребер, контуров и периметра такого многоугольника, представив вам необходимую информацию и подробные примеры.
Разделение составного многоугольника на простые многоугольники
Принципы разбиения сложного многоугольника на простые элементы
В рамках изучения структуры и свойств многоугольников, важным вопросом является разбиение составного многоугольника на простые элементы. Это позволяет упростить анализ и вычисления, а также понять особенности каждого простого многоугольника внутри сложной фигуры.
Простые многоугольники, в отличие от составных, имеют все стороны замкнутыми и не пересекаются. Разделение составного многоугольника на такие простые элементы требует тщательного анализа границ и узловых точек фигуры.
Определение уникальных простых многоугольников
В процессе разбиения сложного многоугольника на простые элементы могут возникать определенные ограничения и правила. Например, простые многоугольники не могут пересекаться друг с другом. При разбиении фигуры необходимо определить такие участки, которые образуют замкнутые перекрывающиеся области.
Алгоритмы разбиения составного многоугольника
Существует несколько алгоритмов, позволяющих разбить сложный многоугольник на простые элементы. Некоторые из них основаны на поиске узловых точек, а другие - на решении системы уравнений, относящихся к границам фигуры. Каждый алгоритм имеет свои особенности и применяется в зависимости от конкретной ситуации и требований.
Примеры разбиения составного многоугольника
Для наглядности рассмотрим несколько примеров разбиения сложного многоугольника на простые элементы. Каждый пример демонстрирует особенности алгоритма и позволяет увидеть, как составной многоугольник разбивается на более простые участки.
Таким образом, разбиение составного многоугольника на простые многоугольники является важным шагом в анализе геометрических фигур. Понимание принципов и применение соответствующих алгоритмов позволяют упростить задачи, связанные с изучением и использованием многоугольников в различных областях науки и практики.
Сложение длин линий, определяющих форму простых геометрических многоугольников
В данном разделе мы рассмотрим способы определения общей длины сторон различных простых многоугольников путем сложения отрезков и линий, образующих их периметр.
У каждого простого многоугольника есть набор конечных отрезков или линий, которые образуют его контур. Изучение и сложение длин этих линий позволяет определить общую длину периметра многоугольника, без представления его в виде шаблона.
Для начала определим понятие аналогичное "сторонам" в контексте простых многоугольников. Длины этих отрезков или линий, содержащихся в контуре многоугольника, вносят свой вклад в общую длину его периметра. Определение простоты многоугольника позволяет применить особые методы для расчета длины его периметра, основанные на линейной геометрии.
Например, для треугольника, а также прямоугольника и квадрата, сумма длин отрезков, составляющих их периметры, равняется общей длине периметра многоугольника. Подобным образом, для других простых многоугольников, можно определить методы сложения длин линий для вычисления их периметра.
Вычисление общего периметра фигуры с помощью сложения длин ее сторон
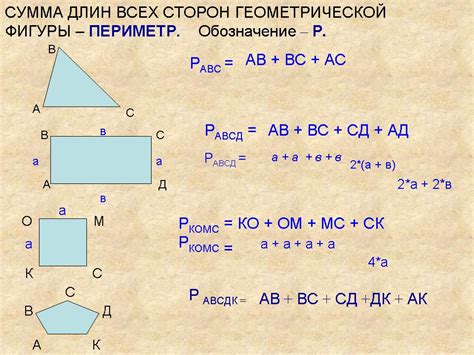
В данном разделе мы рассмотрим примеры, которые помогут вам лучше понять принцип вычисления общего периметра многоугольника посредством сложения длин его сторон. Здесь вы найдете несколько интересных примеров с разнообразными фигурами, где каждый пример поможет вам закрепить и углубить свои знания в этой области.
- Пример с треугольником
- Рассмотрим треугольник со сторонами, длины которых равны 4, 6 и 8 единиц.
- Для вычисления периметра сложим длины всех сторон: 4 + 6 + 8 = 18 единиц.
- Пример с прямоугольником
- Рассмотрим прямоугольник со сторонами, длины которых равны 5 и 9 единиц.
- Для вычисления периметра сложим длины всех сторон: 5 + 5 + 9 + 9 = 28 единиц.
- Пример с пятиугольником
- Рассмотрим пятиугольник со сторонами, длины которых равны 2, 3, 4, 5 и 6 единиц.
- Для вычисления периметра сложим длины всех сторон: 2 + 3 + 4 + 5 + 6 = 20 единиц.
Таким образом, вычисление общего периметра фигуры сводится к простому действию - сложению длин всех ее сторон. Приведенные примеры позволят вам лучше осознать и применить этот принцип на практике. Знание вычисления периметра многоугольника является важной составляющей математического и геометрического анализа различных фигур.
Пример вычисления общей длины граней треугольника на основе формулы
В этом разделе мы рассмотрим применение формулы, позволяющей вычислить сумму длин сторон треугольника. Для этого мы используем значения длин отдельных сторон, которые в нашем случае представляют собой грани этого геометрического объекта. Формула представляет собой способ объединить значения длин сторон в одну общую длину, что помогает нам лучше понять и изучить эту геометрическую фигуру.
| Сторона треугольника | Длина стороны |
|---|---|
| Сторона AB | 10 |
| Сторона BC | 12 |
| Сторона CA | 15 |
В представленной таблице указаны названия сторон треугольника и их соответствующие длины. Чтобы вычислить общую длину граней треугольника, достаточно применить формулу, которая учитывает значения длин отдельных сторон. В нашем примере формула будет выглядеть следующим образом:
Сумма длин сторон треугольника = длина стороны AB + длина стороны BC + длина стороны CA
Подставляя значения длин сторон треугольника, получаем:
Сумма длин сторон треугольника = 10 + 12 + 15 = 37
Таким образом, общая длина граней треугольника в данном примере составляет 37 единиц длины. Это число позволяет нам оценить общую протяженность треугольника и сравнить ее с другими геометрическими объектами.
Вопрос-ответ

Как можно посчитать сумму длин сторон многоугольника?
Для расчета суммы длин сторон многоугольника необходимо измерить каждую сторону и сложить их значения. Длины сторон можно измерить с помощью линейки или другого инструмента для измерения длины.
Какие принципы лежат в основе расчета суммы длин сторон многоугольника?
Основным принципом расчета суммы длин сторон многоугольника является простое сложение длин каждой стороны. Помимо этого, необходимо учесть, что сумма длин сторон многоугольника всегда будет больше длины любой его стороны, но меньше суммы периметров всех треугольников, образованных этим многоугольником.
Можете привести пример расчета суммы длин сторон многоугольника?
Конечно! Рассмотрим пример треугольника. Пусть длины его сторон равны 5 см, 7 см и 9 см. Сумма длин сторон будет равна 5 + 7 + 9 = 21 см. Таким образом, для данного треугольника сумма длин сторон составляет 21 см.



