В мире, где все становится все более сложным и неоднозначным, местоположение играет ключевую роль во многих аспектах нашей жизни. Одно из самых фундаментальных понятий, связанных с местоположением, - это абсциссы и ординаты. Координатная плоскость позволяет нам ориентироваться в пространстве и точно определять положение объектов. Это важное средство, которое находит свое применение в различных сферах, от географии до математики и науки о данных.
Абсциссы и ординаты - это две основные координаты, которые помогают нам определить точное положение объектов на плоскости. Абсцисса - это горизонтальная ось, которая показывает расстояние от начальной точки до конкретной точки вправо или влево. Ордината - это вертикальная ось, которая показывает расстояние от начальной точки до конкретной точки вверх или вниз.
Определение местоположения на координатной плоскости с помощью абсцисс и ординат позволяет нам не только точно указывать положение объектов, но и выполнять различные операции с данными точками. Независимо от того, находимся ли мы в географическом пространстве или работаем с математическими моделями, координатная плоскость является незаменимым инструментом визуализации и анализа информации.
Основные понятия и принципы размещения оси X и оси Y

Для упорядоченной системы координат, существуют основные концепции и принципы, которые определяют положение абсциссы и ординаты. Размещение оси X и оси Y играют важную роль в определении положения точек и объектов на плоскости.
- Принцип первого измерения: ось X представляет горизонтальную ось, где каждая точка обладает своим уникальным значением. Она используется для измерения расстояний по горизонтали и определения положения объектов на плоскости влево или вправо от начальной точки.
- Принцип второго измерения: ось Y представляет вертикальную ось, где каждая точка также имеет свое собственное значение. Она используется для измерения расстояний по вертикали и определения положения объектов на плоскости вверх или вниз от начальной точки.
- Относительное положение: оси X и Y пересекаются в начальной точке, которая обозначается как (0,0). Значение абсциссы положительно справа от начальной точки и отрицательно слева от нее. Значение ординаты положительно выше начальной точки и отрицательно ниже нее.
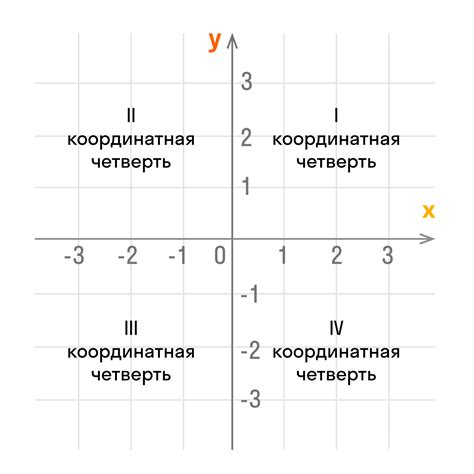
- Первый квадрант: точки с положительными значениями как по оси X, так и по оси Y находятся в первом квадранте, который находится в верхней правой части плоскости.
- Второй квадрант: точки, у которых значение абсциссы отрицательно, а значение ординаты положительно, находятся во втором квадранте, который находится в верхней левой части плоскости.
- Третий квадрант: точки с отрицательными значениями как по оси X, так и по оси Y находятся в третьем квадранте, который находится в нижней левой части плоскости.
- Четвертый квадрант: точки со значениями абсциссы положительными, а значениями ординаты отрицательными, находятся в четвертом квадранте, который находится в нижней правой части плоскости.
Понимание основных понятий и принципов размещения абсциссы и ординаты позволяет легче интерпретировать графические представления, строить графики функций, решать геометрические задачи и применять их в различных областях науки и техники.
Абсцисса и ордината: понятие и взаимосвязь
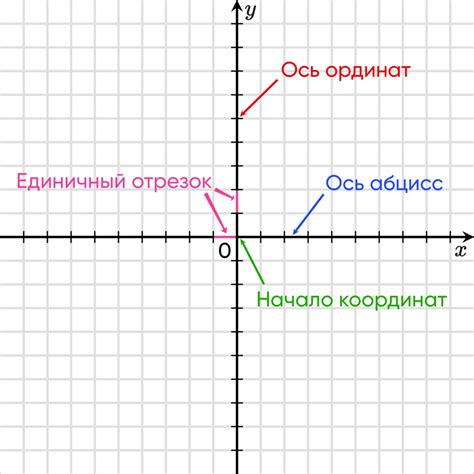
Идея взаимосвязи абсциссы и ординаты заключается в том, что каждая точка на плоскости имеет определенные значения абсциссы и ординаты, которые вместе определяют ее положение. При наличии информации об абсциссе и ординате точки, можно однозначно определить ее координаты.
Абсциссы и ординаты широко применяются в различных областях, таких как математика, физика, графика и география. Например, в математике они используются для построения графиков функций и решения уравнений, в физике - для описания движения тела в пространстве, в графике - для создания компьютерной графики, а в географии - для маркировки местоположения географических точек.
Таким образом, понимание понятия абсциссы и ординаты, а также их взаимосвязи является неотъемлемой частью практических и теоретических задач, требующих работы с двумерными координатами на плоскости.
Оси координат: основные элементы плоскости координат
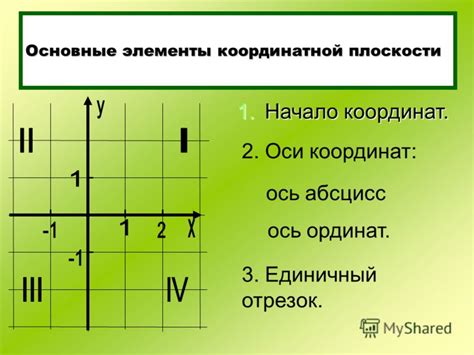
Горизонтальная ось - это одна из осей координатной плоскости, которая ориентирована вперёд и назад. Она также известна как ось абсцисс или ось Х. Горизонтальная ось разделяет плоскость на две части: левую и правую.
Например, координата (-3, 0) будет расположена слева от начала горизонтальной оси, а координата (4, 0) - справа от неё.
Вертикальная ось - это другая ось координатной плоскости, которая ориентирована вверх и вниз. Она также известна как ось ординат или ось Y. Вертикальная ось разделяет плоскость на две части: верхнюю и нижнюю.
Например, точка (0, -2) будет расположена ниже начала вертикальной оси, а точка (0, 5) - выше неё.
Совместно горизонтальная и вертикальная оси позволяют представить положение точек на координатной плоскости и определить их координаты. Знание основных компонентов плоскости координат является важным фундаментом для понимания пространственной геометрии и различных научных и инженерных дисциплин.
Угол между осями: определение и его значение в координатной системе
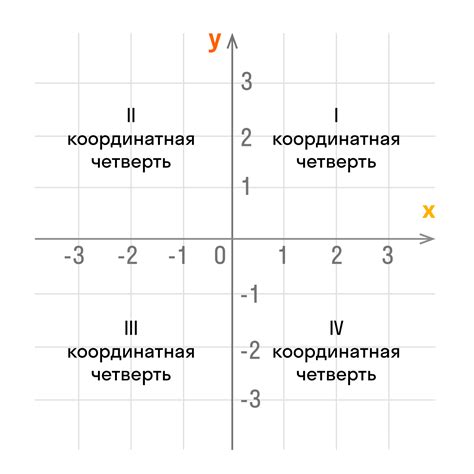
Определение угла между осями имеет прямую связь с распределением значений на графике функции. Этот угол обусловлен структурой координатной системы и играет ключевую роль в определении угла наклона линии графика. Значение угла позволяет определить, какая область графика находится выше или ниже оси абсцисс, а также служит важным инструментом для анализа тенденций и изменений на графике.
Таблица ниже демонстрирует значения угла между осями для различных расположений точек в координатной плоскости:
| Угол между осями | Расположение точек |
|---|---|
| 0° | Точки лежат на оси абсцисс |
| 90° | Точки лежат на оси ординат |
| 45° | Точки расположены в верхнем правом квадранте |
| 135° | Точки расположены в верхнем левом квадранте |
| -45° | Точки расположены в нижнем правом квадранте |
| -135° | Точки расположены в нижнем левом квадранте |
Знание угла между осями позволяет более точно определить положение точек на графике и проводить более детальный анализ их распределения. Это важный элемент в изучении математики, физики, экономики и других дисциплин, где применяются координатные системы.
Нулевая точка: значение и роль в определении координат
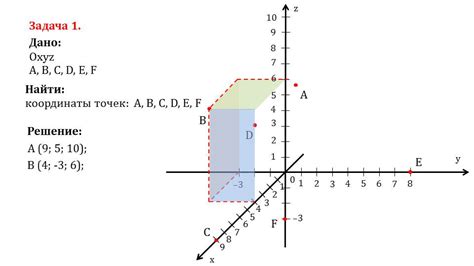
Нулевая точка, также известная как начало координат, является отправной точкой для определения координат. Она обозначается как (0,0) и представляет собой точку, где пересекаются оси абсцисс и ординаты на координатной плоскости.
Роль нулевой точки состоит в том, чтобы задать ось отсчета и ориентировать систему координат. Ось абсцисс, идущая вправо от нулевой точки, представляет положительные значения, а ось ординат, идущая вверх, также имеет положительные значения. Негативные значения отсчитываются влево и вниз соответственно.
Понимание значения нулевой точки дает нам возможность определить положение объектов на координатной плоскости. Используя комбинацию числовых значений абсциссы и ординаты, мы можем указать точное местоположение объекта относительно начала координат.
Равномерная сетка: использование для определения координатных точек
Одним из главных преимуществ использования равномерной сетки является его способность обеспечивать точные и последовательные расположение координатных точек. В отличие от других методов, равномерная сетка предоставляет удобную систему отсчета и ориентирует нас в пространстве.
Построение равномерной сетки основано на принципе размещения равноотстоящих точек в пределах определенного интервала. Такая система координат помогает нам визуализировать и анализировать данные, так как позволяет нам определить положение объектов в двумерном пространстве.
Использование равномерной сетки имеет широкий спектр применения. Она может быть использована в геодезии, картографии, статистике, компьютерной графике и других областях, где требуется точное определение координатных точек.
Поэтому, равномерная сетка является незаменимым инструментом при работе с геометрическими и статистическими данными, позволяя нам упростить и ускорить процесс определения и анализа координатных точек на плоскости.
Использование координат в математике: основные концепции и применения
Применение координат в математике охватывает широкий спектр областей, включая геометрию, алгебру, анализ и многие другие. Создание и использование математических моделей, основанных на координатах, позволяет нам решать сложные задачи, представлять и анализировать данные, а также предсказывать и прогнозировать различные события и явления.
- Геометрия: В геометрии координаты помогают определять положение точек, линий, плоскостей и других геометрических фигур. Они также используются для измерения расстояний и углов между объектами.
- Алгебра: В алгебре координаты используются для решения систем уравнений, нахождения корней полиномов, а также для представления и оперирования с алгебраическими объектами, такими как векторы и матрицы.
- Анализ и дифференциальные уравнения: В анализе и дифференциальных уравнениях координаты играют важную роль в определении производных и интегралов, изучении функций и их графиков, а также в решении задач оптимизации и моделирования.
- Статистика и вероятность: В статистике и вероятности координаты используются для описания и анализа данных, построения графиков, вычисления статистических параметров, а также для моделирования вероятностных событий.
- Физика и инженерия: В физике и инженерии координаты применяются для описания движения объектов, моделирования физических систем, а также для проектирования и анализа различных технических конструкций.
Это лишь некоторые из областей, где применение координат позволяет нам более эффективно изучать и описывать мир вокруг нас. Понимание принципов и концепций координатной системы является важным фундаментом для успешного решения задач в математике и ее приложениях.
Практическое использование координат в повседневной жизни

В реальном мире существует бесчисленное количество ситуаций, в которых мы используем координаты для определения местоположения и ориентации. Наша способность понимать и использовать координаты помогает нам ориентироваться, находить нужные места, планировать путешествия и выполнять различные задачи.
Координаты можно применять в самых разных областях нашей жизни. В навигации, например, мы используем широту и долготу для определения места на земле и путешествия по миру. В графическом дизайне и архитектуре мы определяем положение элементов, создаем планы зданий и схемы помещений. Даже в спорте координаты играют важную роль, когда мы оцениваем положение игроков на поле и стратегии команды.
Важно понимать, что координаты предоставляют нам систему относительности, которая позволяет нам определить положение объекта или места в пространстве. Это универсальный язык, который позволяет нам точно описать и локализовать что-либо. Благодаря использованию координат мы можем легко передвигаться по карте, найти точное местоположение интересного нам места, а также эффективно планировать и организовывать свои действия.
Использование координат в повседневной жизни не только упрощает нашу жизнь, но и открывает новые возможности. Оно помогает нам изучать новые места, создавать и понимать графические изображения, анализировать данные и принимать взвешенные решения. Без координат было бы сложно представить мир вокруг нас, и потому важно осознавать и умело использовать их возможности.
Вопрос-ответ

Какое значение имеют абсцисса и ордината в геометрии?
Абсцисса и ордината - это координаты точки на плоскости и позволяют определить ее положение относительно начала координат.
Как можно найти местоположение абсциссы и ординаты на графике?
Для определения местоположения абсциссы и ординаты на графике необходимо провести перпендикулярные оси координат, где абсцисса обозначает горизонтальное положение, а ордината - вертикальное положение точки.
В каких областях науки и техники применяются абсциссы и ординаты?
Абсциссы и ординаты находят широкое применение в геометрии, физике, математике, инженерии, компьютерной графике и других областях науки и техники. Они используются, например, для построения графиков функций, решения уравнений, моделирования объектов и траекторий движения.
Какие основные принципы определения абсциссы и ординаты?
Основные принципы определения абсциссы и ординаты включают выбор начала координат, измерение расстояний от начала координат и использование знаков плюс и минус для указания положения точки относительно осей. Например, если точка находится правее начала координат, ее абсцисса будет положительной, а если точка находится выше начала координат, ее ордината будет положительной.