Перед нами требование продемонстрировать, что треугольник может быть прямоугольным, если он вписан в окружность. Изучение данной теоремы заставляет нас вглядеться в глубины геометрических форм и искать связи между ними. Пожалуй, одним из самых увлекательных аспектов математики является поиск косвенных доказательств, которые позволяют утверждать то, что сразу на глаза или с доступными нам инструментами не видно.
В этой статье мы рассмотрим несколько методов, чтобы приблизиться к финальному ответу и поблагодарить открытые умы великих ученых, которые открывали нам глаза на необычные связи в геометрии. Мы рассмотрим фундаментальные понятия, такие как углы, стороны, радиус, хорды и использование технологий для доказательства. Чтобы вникнуть в глубину математической мысли, нам понадобится умение сосредоточиться и анализировать каждый момент.
Подобные исследования находят применение не только в математике, но и в реальном мире: от архитектуры и конструирования до физики и астрономии. Развивая способность логическо-математического мышления, мы обогащаем нашу жизнь не только научными открытиями, но и понимаем гармонию, которая лежит в основе нашего мира. Готовы ли Вы отправиться вместе с нами в увлекательный мир геометрии и математического творчества?
Основные принципы определения прямоугольности треугольника в окружности
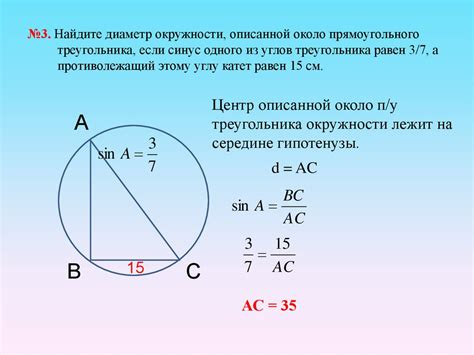
- Используйте теорему о вписанных углах: если два угла треугольника, образованные хордой, равны между собой, то треугольник прямоугольный.
- Примените свойства равномерно распределенных углов: если хорда, соединяющая две точки на окружности, делит остальные дуги на две равные части, то треугольник прямоугольный.
- Изучите касающуюся хорду: если хорда является диаметром окружности, то треугольник обязательно прямоугольный.
Совокупное использование этих основных идей позволяет провести анализ и определить прямоугольность треугольника в окружности.
Метод 1: применение свойств перпендикуляров и хорд
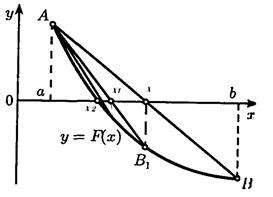
В данном разделе будет представлен метод, позволяющий доказать прямоугольность треугольника, образованного в окружности, с использованием свойств перпендикуляров и хорд.
- Построим треугольник ABC внутри окружности, а также проведем диаметр AB.
- Опустим перпендикуляр CD из вершины C на сторону AB.
- Используя свойства перпендикуляров, утверждаем, что угол ACB является прямым углом, так как угол между перпендикуляром и хордой, опущенным из общей точки (вершины C), всегда является прямым углом.
- Далее, применяя свойства перпендикуляров и хорд, утверждаем, что углы CAB и CBA также являются прямыми углами.
- Таким образом, треугольник ABC обладает тремя прямыми углами и является прямоугольным треугольником.
Шаг 1: выявление двух пересекающихся хорд, образующих прямые углы

Для определения таких хорд, исследуйте окружность и обратите внимание на две линии, которые пересекаются в одной точке и создают прямые углы. Важно отметить, что эти хорды должны быть перпендикулярными друг другу, что означает, что их угол встречи равен 90 градусам.
Шаг 2: исследование равенства дуг
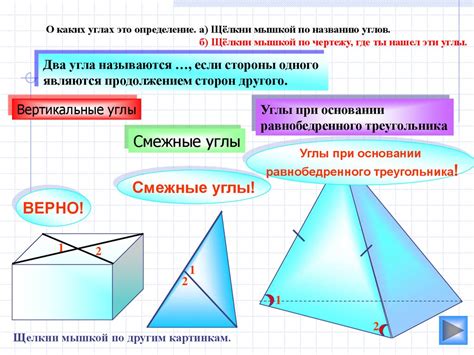
Приступая к проверке равенства дуг вокруг окружности в контексте доказательства прямоугольности треугольника, мы сосредотачиваемся на определении схожести величин этих дуг.
Для проведения данной проверки мы анализируем соответствующие углы и дуги, образующиеся внутри окружности, и сравниваем их между собой. Основываясь на свойствах геометрических фигур, мы ищем пары равных дуг, которые имеют одинаковые центральные углы.
Взаимное равенство дуг указывает на симметрию треугольника относительно окружности. Если мы обнаружим две равные дуги, формирующие угол равенство величин, то это может быть первым шагом в доказательстве прямого угла в треугольнике, который описывает окружность.
Необходимо учитывать различные свойства окружности, чтобы грамотно провести проверку равенства дуг. При обнаружении равных дуг и соответствующих углов, мы можем продвинуться к следующим шагам в процессе доказательства прямоугольности треугольника и использованию данной информации для определения прямого угла в окружности.
Шаг 3: применение свойства перпендикуляров
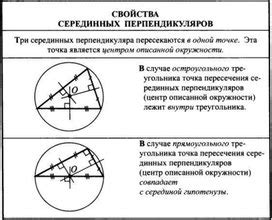
Метод 2: применение теоремы о равенстве углов

В данном разделе рассматривается один из методов доказательства прямоугольности треугольника вписанного в окружность с использованием теоремы о равенстве углов.
Для начала, представим треугольник, вписанный в окружность, и рассмотрим его углы. Один из углов треугольника, обозначим его как угол А, лежит на дуге окружности, а остальные два угла, обозначим их как углы B и C, лежат на хордах, соединяющих точки пересечения этой дуги с остальными сторонами треугольника.
Согласно теореме о равенстве углов, если два угла треугольника, лежащие на хордах окружности, равны между собой, то дуги, соответствующие этим углам, тоже равны. Это означает, что если угол B и угол C в треугольнике вписанном в окружность равны между собой, то дуги AB и AC на окружности имеют одинаковую длину.
Таким образом, применяя теорему о равенстве углов, можно доказать прямоугольность треугольника вписанного в окружность, основываясь на равенстве между углами B и C.
Шаг 1: Приобретение двух различных углов

Пример: Угол А и угол В являются двумя различными углами, которые мы получаем из исходного треугольника. Используя геометрические принципы и свойства окружности, мы можем определить, что эти два угла не равны друг другу. Например, угол А может быть аккуратным углом, а угол В - тупым. Это позволит нам начать доказательство и исследовать другие углы и стороны треугольника впоследствии.
Для получения двух неравных углов мы можем использовать различные методы, такие как измерение углов с помощью графической программы или использование геометрических формул для вычисления значений углов на основе известных данных. Важно отметить, что точность полученных углов будет зависеть от точности исходных данных и используемых методов измерения.
Вопрос-ответ

Как можно доказать, что треугольник является прямоугольным в окружности?
Для доказательства того, что треугольник прямоугольный в окружности, можно использовать несколько методов. Один из них - использование теоремы о центральном угле. Если в треугольнике есть угол, центральный для дуги, которая является диаметром окружности, то треугольник будет прямоугольным, и противолежащая этому углу сторона будет являться диаметром окружности. Или же можно использовать теорему о равенстве остроугольных треугольников, где прямоугольники равны по гипотенузе и катету.



