Магические числа, которые скрываются в круговой царстве тригонометрии, заботливо окружают нас с самого рождения. Они столь привычны, что мы даже не задумываемся о том, как и почему они так уверенно сопровождают наши жизни. То, что некоторые называют "секретами" синуса и косинуса, на самом деле является сложным и интригующим миром математических закономерностей и непостижимой гармонии.
В этом особом уголке математических знаний традиционные определения покажутся вам вторичными, ведь здесь мы присоединяемся к философской стороне размышлений, раскрывая глубину круга и его удивительных свойств. Мы приглашаем вас исследовать происхождение этих грациозных функций и увидеть, как они изменяются, приспосабливаются и эволюционируют, отражая всемирный порядок и гармонию природы.
Соприкосновение с изяществом синуса и косинуса на окружности обещает не только математическое развлечение, но и неоценимую пользу в различных сферах нашего существования. Здесь вы сможете узнать, как эти функции с легкостью решают сложные задачи, связанные с геометрией, физикой и инженерным проектированием. Готовьтесь к тому, чтобы увидеть насколько широкой и практической может быть область применения этого могущественного дуэта тригонометрии.
Описание сущности и функции тригонометрических функций на геометрическом объекте
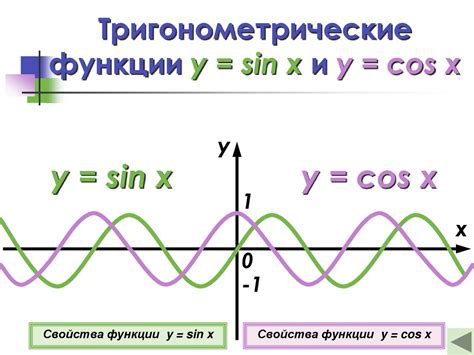
Для полного понимания природы и применения тригонометрических функций связанных с геометрическим объектом, крайне полезно ознакомиться с концепцией синуса и косинуса на окружности. Именно эти функции позволяют нам описать и прогнозировать различные явления и зависимости в мире геометрических форм и фигур.
Синус окружности - это математическая функция, которая связывает угол и отношение длины противоположного катета к гипотенузе при прямоугольном треугольнике, образованном радиусом окружности и смежным катетом. Это означает, что синус окружности может быть представлен как отношение длины противоположного катета к длине радиуса этой окружности.
Синус окружности также может рассматриваться как вертикальная координата точки на окружности, полученная путем проекции радиуса на ось координат.
В то же время, косинус окружности - это функция, которая связывает угол и отношение длины прилежащего катета к гипотенузе при том же прямоугольном треугольнике на окружности. Как и синус, косинус также может быть представлен как отношение длины прилежащего катета к длине радиуса окружности.
Косинус окружности также может рассматриваться как горизонтальная координата точки на окружности, полученная путем проекции радиуса на ось координат.
Знание и понимание синуса и косинуса на окружности открывают нам возможность решать сложные геометрические задачи, а также применять эти функции в физике, инженерии и других научных областях для определения зависимостей и решения различных проблем.
Важное правило: сумма квадратов синуса и косинуса

В данном разделе мы рассмотрим важное правило, связанное с синусом и косинусом, которое позволяет нам выразить сумму квадратов этих функций через конкретные значения на окружности.
Для начала приведем основные определения. Синус и косинус - это тригонометрические функции, которые связаны с углом между осью x и радиусом, проведенным к точке на окружности.
Итак, важное правило гласит: сумма квадратов синуса и косинуса любого угла на окружности всегда равна 1. Другими словами, sin^2(α) + cos^2(α) = 1, где α - угол на окружности.
Это правило имеет широкое применение в различных областях, таких как физика, инженерия, геометрия и другие. Например, оно позволяет нам вычислить одну тригонометрическую функцию, зная значение другой.
Для более наглядного представления можно использовать таблицу, в которой будут приведены значения синуса и косинуса для различных углов. Такая таблица поможет нам легко проверить справедливость данного правила.
| Угол (α) | Синус (sin(α)) | Косинус (cos(α)) |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 0.5 | 0.866 |
| 45° | 0.707 | 0.707 |
| 60° | 0.866 | 0.5 |
| 90° | 1 | 0 |
Как видно из таблицы, сумма квадратов синуса и косинуса для каждого угла равна 1, что подтверждает данное важное правило.
Как определить значения синуса и косинуса для заданного угла
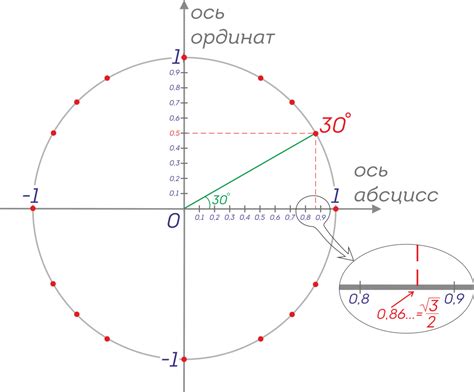
В данном разделе мы рассмотрим методы для определения значений синуса и косинуса для заданного угла без использования специфических формул и детальных математических расчетов. Мы представим простые шаги, которые помогут вам вычислить синус и косинус угла, используя синонимы и общепонятные примеры.
1. Используйте таблицу значений: воспользуйтесь таблицей значений синуса и косинуса, которая представляет собой удобный инструмент для быстрого определения значений данных функций при различных углах. По заданному углу найдите соответствующие значения для синуса и косинуса в таблице.
2. Используйте геометрические соотношения: использование геометрических связей между углами и сторонами треугольника может помочь в определении значений синуса и косинуса. Например, рассмотрите прямоугольный треугольник, где один из углов известен, а значения двух сторон треугольника известны или могут быть измерены. По формуле отношения сторон определите значения синуса и косинуса.
3. Используйте специализированные математические приложения: существует множество программ и приложений, которые могут автоматически вычислять значения синуса и косинуса для заданного угла. Используйте эти ресурсы для более точного и быстрого определения значений функций.
Используя эти методы, вы сможете легко определить значения синуса и косинуса для заданного угла без необходимости проведения сложных математических расчетов. Знание этих значений может быть полезно во множестве задач из различных областей, включая астрономию, физику, инженерию и т.д.
Методы расчета значений синуса и косинуса на различных углах
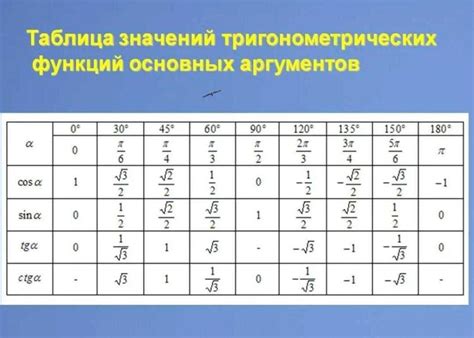
В данном разделе мы рассмотрим примеры расчетов значений синуса и косинуса для различных углов. С помощью данных методов, мы сможем определить значения этих тригонометрических функций для конкретных углов без использования сложных формул и таблиц.
1. Расчет синуса и косинуса для острых углов.
Для острых углов, меньших 90 градусов, мы можем использовать следующий способ расчета. Возьмем, например, угол 30 градусов. Для рассчета значения синуса и косинуса данного угла, мы делим длину противолежащего и прилежащего катетов прямоугольного треугольника на его гипотенузу. Таким образом, получим значения функций синус и косинус угла 30 градусов.
2. Расчет синуса и косинуса для тупых углов.
Для тупых углов, больших 90 градусов, мы также можем применить рассмотренный выше метод, однако необходимо учесть изменение знака значений синуса и косинуса. Например, для угла 120 градусов, мы также делим длину противолежащего и прилежащего катетов на гипотенузу, но при этом учитываем, что значения синуса и косинуса будут отрицательными.
3. Расчет синуса и косинуса для прямого угла.
При расчете значений синуса и косинуса для прямого угла (90 градусов), значенияю функций будут просто равны 1 и 0 соответственно. Это связано с особенностью геометрической постановки задачи и свойствами прямоугольных треугольников.
Используя описанные методы, мы можем легко и быстро рассчитывать значения синуса и косинуса для конкретных углов без углубления в сложные математические выкладки и формулы.
Рациональное применение тригонометрических функций в геометрии
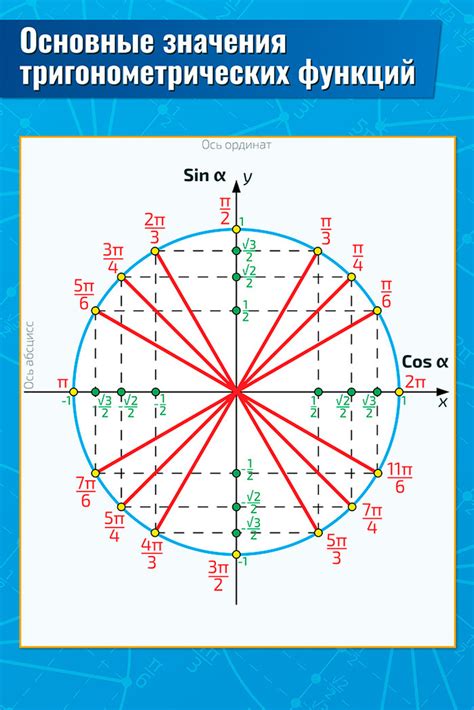
При использовании синуса и косинуса в геометрии полезно предварительно определить цель и понять, какая информация вам нужна. Например, если вы ищете длину незнакомой стороны треугольника, вы можете использовать теорему косинусов. Если же вам необходимо найти угол между двумя сторонами треугольника, может пригодиться теорема синусов. Правильное применение этих функций поможет вам решить задачу более эффективно и точно.
Однако, важно помнить, что использование синуса и косинуса требует осторожности. При работе с углами следует учитывать их меру – градусы или радианы. Это особенно важно при переходе от одной системы измерения к другой, чтобы избежать путаницы и ошибок в результатах расчетов.
Кроме того, синус и косинус широко применяются в построении геометрических фигур и моделировании. С их помощью можно находить координаты точек на плоскости, определять расстояния и углы между объектами, а также строить кривые и плоскости. Это открывает широкие возможности для решения разнообразных задач и создания новых геометрических конструкций.
Значение тригонометрических функций при решении физических задач

В физике синус и косинус широко используются при решении различных задач, связанных с движением, колебаниями и волными процессами. Знание значений синуса и косинуса на окружности позволяет нам анализировать и определять связь между различными физическими величинами.
Синус и косинус являются тригонометрическими функциями, которые зависят от угла, образованного радиусом окружности и горизонтальной осью. В физических задачах они позволяют нам определить отклонение от равновесного положения, амплитуду колебаний, скорость изменения величин и многое другое.
Например, при изучении гармонических колебаний с помощью синуса и косинуса мы можем определить максимальное смещение от положения равновесия, период колебаний и фазу колебаний. Для задач о движении по окружности с использованием тригонометрических функций можно определить радиальную и тангенциальную составляющие скорости, ускорение и силы.
Синус и косинус широко применяются в физике при расчетах траекторий движения тел, при анализе электромагнитных колебаний и волн, а также при изучении оптики и звуковых явлений. Знание значений синуса и косинуса позволяет нам получить количественную оценку и представление о многих физических величинах и процессах.
Как определить угол, зная значения синуса и косинуса
- Способ 1: Использование синуса
- Способ 2: Использование косинуса
- Способ 3: Использование соотношений между синусом и косинусом
Зная значение синуса угла, можно использовать обратную функцию arcsin, чтобы определить величину самого угла. Для этого необходимо найти в таблице или использовать калькулятор, который предоставляет возможность расчета arcsin. Подставляем значение синуса в функцию и получаем результат - величину угла.
Аналогично синусу, можно использовать обратную функцию arccos для определения угла по значению косинуса. Для этого необходимо найти в таблице или использовать калькулятор, который предоставляет возможность расчета arccos. Подставляем значение косинуса в функцию и получаем результат - величину угла.
Если известны значения и синуса, и косинуса, можно воспользоваться соотношениями между ними для определения угла. Например, если известно, что sin(угол) = 0.6, а cos(угол) = 0.8, то можно воспользоваться следующей формулой: угол = atan2(sin(угол), cos(угол)). Подставляем значения и получаем искомую величину угла.
Зная значения синуса и косинуса угла, мы можем использовать различные методы для определения его величины. Эти методы основаны на использовании обратных функций arcsin и arccos, а также на соотношениях между синусом и косинусом. Зная эти принципы, мы можем решать задачи на нахождение угла без использования его изначального значения.
Применение тригонометрических функций в уравнениях

В данном разделе мы рассмотрим применение синуса и косинуса в тригонометрических уравнениях. Уравнения, содержащие синус и косинус, возникают в различных областях науки и техники, таких как физика, электротехника, механика и другие.
Тригонометрические уравнения позволяют решать задачи, связанные с измерением углов и рассмотрением периодических явлений. Они позволяют найти значения неизвестных углов или длин сторон треугольников, основываясь на свойствах синуса и косинуса.
Важно знать, что синус и косинус - это функции, значения которых меняются от -1 до 1. Они зависят от значения угла, заданного в радианах, и представляют собой отношение сторон прямоугольного треугольника.
В тригонометрических уравнениях полезно применять свойства синуса и косинуса, такие как периодичность, четность и нечетность функций, а также соотношения между ними. Это помогает сократить уравнение, выражая его через одну из функций и находя нетривиальные решения.
Таблицы синусов и косинусов помогают найти значения функций при заданных углах. Они позволяют упростить процесс решения уравнений, облегчая вычисления и избегая ошибок при оценке значений функций.
Применение тригонометрических уравнений в различных областях позволяет решать сложные задачи, связанные с динамикой, колебаниями, измерением углов и другими явлениями. Понимание и умение применять синус и косинус существенно облегчают решение таких задач и повышают точность полученных результатов.
| Угол, градусы | Синус | Косинус |
|---|---|---|
| 0 | 0 | 1 |
| 30 | 0.5 | 0.87 |
| 45 | 0.71 | 0.71 |
| 60 | 0.87 | 0.5 |
| 90 | 1 | 0 |
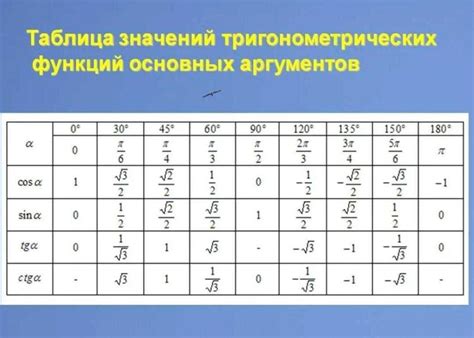
Таблица значений синуса и косинуса для углов, применяемых чаще всего
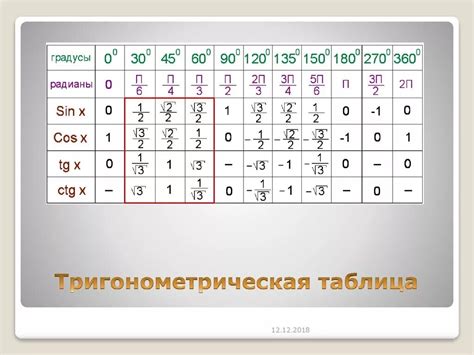
Таблица значений синуса и косинуса представляет собой удобный инструмент для быстрого и точного определения значений этих тригонометрических функций. Используя данную таблицу, можно найти значения синуса и косинуса для конкретного угла без необходимости повторных расчетов.
В таблице приведены значения синуса и косинуса для углов, выраженных в градусах. Также предоставлены эквивалентные значения углов в радианах для более удобной работы. Эта таблица позволяет быстро находить значения синуса и косинуса для стандартных углов, таких как 0°, 30°, 45°, 60° и 90°, а также для их комбинаций.
Знание таблицы значений синуса и косинуса позволяет упростить вычисления и убедиться в правильности результатов. Регулярное использование данной таблицы поможет закрепить навыки работы с тригонометрическими функциями и повысить точность расчетов.
Смысл синуса и косинуса в компьютерном программировании
В программировании существует широкий спектр применений для синуса и косинуса, двух математических функций, которые изначально связываются с геометрическими свойствами окружности. В данном разделе мы рассмотрим, как эти функции используются в компьютерных программных средах и как их значения могут быть полезны для различных задач и расчетов.
В основе многих алгоритмов и программных модулей лежат вычисления, связанные с геометрией и тригонометрией. Значение синуса и косинуса может быть применено для нахождения углов и координат точек в двумерном и трехмерном пространствах, а также для моделирования движения и взаимодействия объектов.
Чтобы вычислить синус и косинус определенного угла, используются числовые методы, включая ряды Тейлора и приближенные алгоритмы. Результаты этих вычислений могут быть представлены в виде десятичных дробей или вещественных чисел и могут служить важными параметрами для работы с графикой, анимацией, физикой и другими областями.
Синус и косинус также полезны для решения задачи работы с векторами и матрицами. Они используются для преобразования координат, поворотов, масштабирования и трансформаций объектов. Благодаря своей связи с геометрией, эти функции могут быть удобным инструментом при работе с трехмерными моделями, виртуальной реальностью и компьютерной графикой в целом.
В области компьютерного программирования синус и косинус могут быть использованы для решения ряда конкретных задач, таких как определение расстояния между координатами на плоскости или в пространстве, вычисление угловой скорости и перемещения объектов, а также для работы с треугольниками и другими геометрическими фигурами. Эти функции демонстрируют свою важность и широкое применение во многих программных продуктах и проектах, где точность и эффективность представляют большое значение.
- Вычисление углов
- Моделирование движения объектов
- Работа с графикой и анимацией
- Работа с векторами и матрицами
- Решение задач геометрии и физики
Вопрос-ответ

Для чего нужны синус и косинус на окружности?
Синус и косинус на окружности являются основными тригонометрическими функциями, которые широко применяются в математике, физике и других науках. Они помогают решать задачи, связанные с геометрией, динамикой, электричеством и многими другими областями. Кроме того, синус и косинус также имеют важное значение при работе с графиками функций, в оптике и обработке сигналов.
Как вычислить значения синуса и косинуса на окружности?
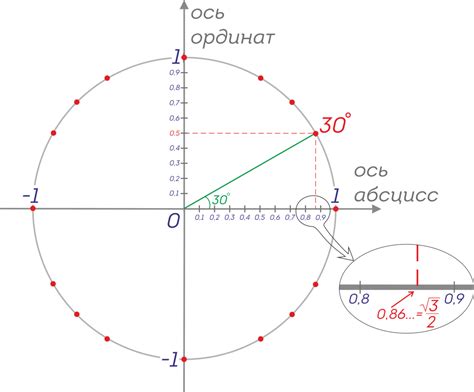
Значения синуса и косинуса на окружности могут быть вычислены с использованием так называемого единичного круга. Для этого на единичной окружности отмечаются точки, образующие углы, равные значению аргумента функции синуса или косинуса. Затем находятся соответствующие координаты этих точек по оси абсцисс и ординат. Например, для угла 30 градусов значения синуса и косинуса будут равны 0.5 и 0.866 соответственно.
Как использовать синус и косинус на окружности для решения геометрических задач?
Синус и косинус на окружности позволяют решать различные геометрические задачи, связанные с треугольниками и другими фигурами. Например, с их помощью можно находить длины сторон и углы треугольника, расстояние между точками на плоскости и многое другое. Для этого нужно знать значения синуса и косинуса для соответствующих углов и применять соответствующие тригонометрические формулы.
Можно ли рассчитать значения синуса и косинуса на окружности программно?
Да, значения синуса и косинуса на окружности могут быть рассчитаны при помощи программного кода. Для этого можно использовать различные математические библиотеки, которые предоставляют функции для вычисления тригонометрических значений. Например, в языке программирования Python существует библиотека math, которая содержит функции sin() и cos(), принимающие аргументы в радианах и возвращающие значения синуса и косинуса соответственно.