Возможно, многие из нас задумывались о том, откуда берутся числа, которые окружают нас в повседневной жизни. Они везде – счетная машина банковского терминала, ошибка в расчете количества продуктов в сумке из магазина, или же даже разности в расписаниях прилетов и отправлений на нашем ходульном телефоне. Мы не задумываемся откуда они берутся или как мы оказываемся перед ними в силу очевидности или отсутствия других вариантов.
Однако, мало кто задался вопросом о происхождении математических принципов, лежащих в основе всех этих чисел и формул, без которых наш мир не смог бы функционировать так, как мы привыкли. Именно математика – это язык, на котором зашифрованы все законы физики, информатики, экономики и других наук. Она – крупнейший инструмент человечества для измерения, вычисления и объяснения мира, в котором мы живем.
Однако, несмотря на все широту ее применения и наслоение множества различных областей знаний и новых открытий, математическое исследование при обыденном восприятии не превратилось в навязанный цикл изучения: школа-университет-научный институт. Математика как искусство овладения логическим мышлением и работы с формулами, стала неотъемлемой частью каждого человека, абсолютной необходимостью при решении простых задач и справлении с сложными проблемами.
Финансы и бюджетирование: роль математики в управлении деньгами

Когда дело касается управления финансами и планирования бюджета, математика играет незаменимую роль. Без использования математических принципов и методов, сложно представить себе эффективное управление денежными средствами и достижение финансовых целей.
Математика используется для расчета различных финансовых показателей, включая доходы, расходы, инвестиции, проценты, налоги, и многое другое. Основные математические операции, такие как сложение, вычитание, умножение и деление, применяются для бюджетирования и контроля финансового состояния. Кроме того, использование различных формул и алгоритмов позволяет прогнозировать будущие финансовые показатели и принимать решения на основе числовых данных.
Одной из важных областей, где математика применяется в финансах, является инвестиционный анализ. Математические модели и методы позволяют оценить риски и доходность различных инвестиционных инструментов, и определить наиболее оптимальный портфель, который обеспечит максимальную отдачу при минимальных рисках.
Использование математики также позволяет эффективно планировать бюджет и контролировать расходы. Анализ бюджета и доходов позволяет определить, какую долю доходов следует выделять на жилищные расходы, питание, транспорт, развлечения и другие категории, чтобы обеспечить баланс и избежать долгов. Математические расчеты позволяют создать бюджетную систему, которая позволяет эффективно планировать и используют доходы, а также прогнозировать возможные финансовые трудности и принимать меры по их предотвращению.
В итоге, математика является неотъемлемой частью управления финансами и бюджетирования, помогая принимать обоснованные решения и достигать финансовой стабильности и благополучия.
Размеры и пропорции в строительстве
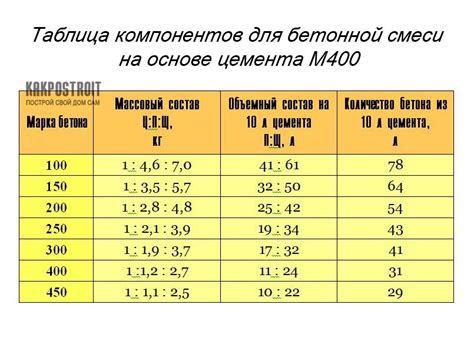
Математика используется при определении размеров фундаментов, стен, окон и дверей, а также при расчете пропорций внутреннего пространства здания. При проектировании строительных объектов, инженеры и архитекторы применяют геометрию, алгебру и тригонометрию, чтобы достичь симметрии и гармонии в каждой детали здания.
Например, при планировке помещений используются математические расчеты для определения оптимального расположения мебели и соотношения между пространствами. Правильные пропорции помогают создать комфортное и функциональное пространство, а несоблюдение пропорций может привести к неэффективному использованию площади или даже ухудшению условий для жизни и работы.
Кроме того, математика необходима при расчете материалов и стоимости строительства. Путем применения математических операций, анализа данных и учета разных факторов, можно определить необходимое количество строительных материалов и рассчитать примерную стоимость проекта.
Таким образом, использование математики и правильное применение размеров и пропорций являются неотъемлемой частью строительства и позволяют создавать надежные, функциональные и эстетически приятные здания.
Построение графиков и анализ данных
Анализ данных включает в себя сбор, обработку и интерпретацию информации в числовой форме. Он позволяет выявлять тренды, зависимости и особенности в данных, что может быть полезно для прогнозирования будущих событий или определения проблем в производстве или бизнесе.
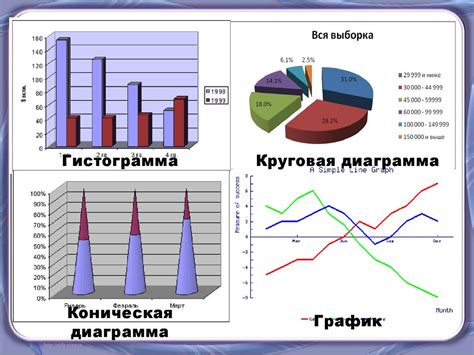
Построение графиков – это визуализация данных с помощью графических представлений, таких как линейные графики, столбчатые диаграммы или круговые диаграммы. Графики позволяют увидеть изменения в данных со временем, сравнить разные наборы данных и выявить аномалии или выбросы.
Примеры применения математического анализа данных и построения графиков в повседневной жизни многообразны: в науке и исследованиях, маркетинге и рекламе, финансах и инвестициях, здравоохранении и медицине, а также в управлении ресурсами и прогнозировании погоды.
С помощью анализа данных и графиков мы можем лучше понять мир вокруг нас, выявить закономерности и оптимизировать нашу жизнь и работу в различных сферах деятельности. Поэтому владение математикой и умение использовать ее методы и инструменты являются важными навыками в современном мире, где информация играет ключевую роль для принятия решений.
Реальные проявления геометрии в нашем окружении

Одним из ярких примеров геометрии в реальной жизни является архитектура. Здания возводятся согласно строгим геометрическим принципам: прямоугольные планировки, параболические арки, идеальные окружности в росписях куполов. Геометрия помогает архитекторам создавать эстетически привлекательные и функциональные сооружения, где каждая деталь представляет собой высокое математическое искусство.
Еще одним примером геометрии, неотъемлемо присутствующей в нашей повседневной жизни, является транспорт. Дороги, мосты, туннели, самолеты и автомобили - все они созданы с использованием геометрических принципов и формул. Геометрия помогает инженерам строить безопасные и эффективные системы передвижения, где расчеты углов, длин и площадей играют важную роль в обеспечении комфортной и безопасной поездки.
Также геометрия присутствует в искусстве. Картины, скульптуры, архитектурные сооружения - все они воплощают геометрические формы и пропорции, которые создают ощущение гармонии и красоты. Используя геометрию, художники и дизайнеры создают впечатляющие произведения, которые возбуждают наши чувства и вызывают эстетическое наслаждение.
Таким образом, геометрия не только является основой математики, но и проникает во все аспекты нашей повседневной жизни. Она помогает создавать красивые и функциональные сооружения, обеспечивает безопасность транспорта и воплощает красоту в искусстве. Понимание геометрии позволяет нам лучше познавать и воспринимать окружающий нас мир.
Расчеты расстояний и времени в путешествиях
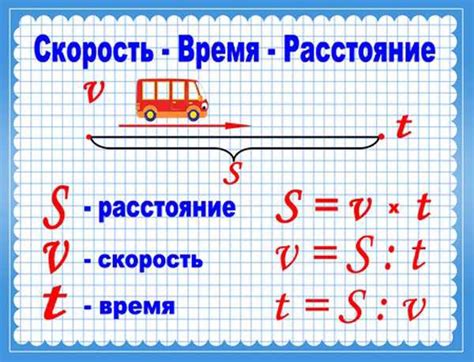
Одной из важных задач в путешествиях является определение расстояния между двумя точками. Для этого мы можем использовать формулу расстояния, основанную на геометрии. Это позволяет нам оценить протяженность пути и выбрать оптимальный маршрут. Кроме того, расчет расстояний также может быть полезен для определения стоимости топлива или билетов на общественный транспорт.
Помимо расстояний, мы также должны учитывать время, необходимое для путешествия. Здесь математика приходит на помощь с расчетом скорости движения. Независимо от того, на каком транспорте мы путешествуем, зная скорость, мы можем оценить время, которое займет нам путешествие от одной точки к другой. Это также помогает нам определить оптимальное время отправления, чтобы избежать пробок или задержек.
Математика также играет важную роль при вычислении средней скорости и прогнозировании прибытия. Например, если мы знаем, что до нашего места назначения осталось 200 км и мы движемся со скоростью 80 км/ч, мы можем легко рассчитать, что при данной скорости мы прибудем туда через 2.5 часа. Такие расчеты помогают нам оптимизировать наше время и составить реалистичные планы.
Расчеты во время покупок: искусство получения скидок и выгодных предложений

Каждый из нас сталкивался с ситуацией выбора между различными товарами на прилавках магазинов. Однако интересно задуматься, как математика помогает нам принять рациональное решение и получить максимальную выгоду от покупок? В этом разделе мы рассмотрим, как расчеты и простые математические операции позволяют умело маневрировать с ценами, скидками и акциями.
С помощью знаний математических принципов мы можем планировать свои покупки, проводить анализ акций и расчеты стоимости товаров с учетом скидок. Кроме того, умение моментально сравнивать цены и применять математические формулы позволяет нам оценить, действительно ли предложение является выгодным или оно лишь кажется таким.
Для начала, давайте рассмотрим простой пример. У вас есть два предложения на одну и ту же позицию: скидка 20% на первом и 30% на втором. Какое из них будет наиболее выгодным для вас? Многие автоматически выберут предложение с большей скидкой, но это не всегда правильный подход. Чтобы понять, какая скидка дает большую экономию, необходимо применить простую математику и вычислить итоговую цену после скидки.
Другим важным аспектом при расчетах покупок является сравнение стоимости товаров разных объемов и упаковок. С помощью математических операций мы можем оценить, какой вариант будет более выгодным для нас – покупка большего количества товара в одной упаковке или нескольких меньших упаковок того же товара с учетом стоимости на единицу товара.
Не менее важно уметь считать доли скидок и проценты, чтобы не попасть в ловушку маркетинговых ходов магазинов. Математические принципы позволяют нам проводить точные расчеты и понимать, насколько цена товара имеет реальную скидку, а не является просто "зацепкой". Это помогает нам принимать обдуманные решения и избегать пустых трат.
В завершение, математика имеет огромное значение при расчетах налогов, чаевых или долей счетов в ресторанах и кафе. Способность оперативно производить арифметические операции и делить сумму на несколько частей позволяет нам уверенно и справедливо делить расходы между участниками группы.
Таким образом, математика играет незаменимую роль в нашей повседневной жизни, особенно при покупках и применении скидок. Она помогает нам принимать рациональные и обоснованные решения, получать наибольшую выгоду от покупок и избегать ненужных трат. Умение применять математические принципы дает нам возможность стать умными потребителями и находить баланс между расходами и экономией.
Оценка вероятностей и рисков
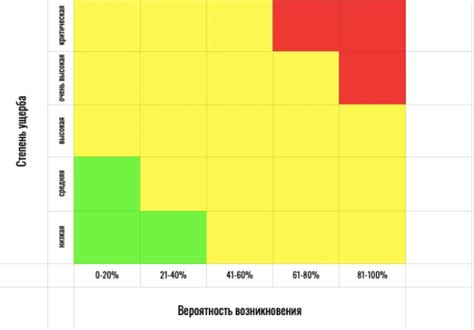
Оценка вероятностей позволяет нам оценить, насколько вероятно возникновение определенного события. Математические методы, такие как статистика и теория вероятностей, помогают проводить анализ данных и на основании полученных результатов делать прогнозы будущих событий.
Риск же, по сути, является связанным с неопределенностью потерей или неблагоприятным исходом. Он может быть измерен с помощью вероятностей и подвергаться оценке. Оценка рисков позволяет оценить, какие последствия можем понести при принятии определенных решений и какие шаги можно предпринять для снижения негативных последствий.
К примеру, при покупке недвижимости мы сталкиваемся с риском возникновения различных факторов, таких как изменение рыночной стоимости, юридические проблемы и т. д. Оценка рисков позволит нам сделать информированный выбор и снизить возможность финансовых потерь.
Таким образом, оценка вероятностей и рисков является неотъемлемой частью нашей повседневной жизни и помогает нам принимать обоснованные решения, минимизируя возможные негативные последствия. Математика играет ключевую роль в этом процессе, обеспечивая нам инструменты для анализа, оценки и прогнозирования вероятностей различных событий.
Прогнозирование погоды и климатических изменений
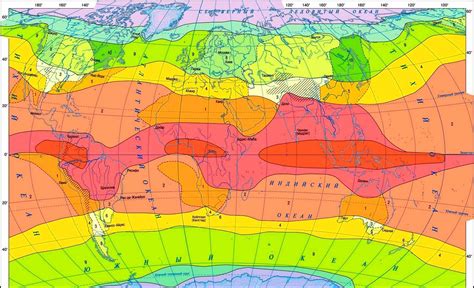
Один из ключевых аспектов прогнозирования погоды связан с анализом огромных объемов данных, полученных от метеорологических станций, спутников и других источников. С помощью математических алгоритмов и статистических моделей, мы можем обрабатывать эти данные и выявлять паттерны и закономерности, которые помогают нам понять текущие погодные условия и сделать предсказания о будущих изменениях.
Кроме того, визуализация данных о погоде и климате также играет важную роль. С помощью математических методов мы можем создавать графики, диаграммы и карты, которые позволяют наглядно представлять информацию о погодных условиях, климатических трендах и географическом распределении различных параметров.
Математическое моделирование также является неотъемлемой частью работы метеорологов и климатологов. Мы используем уравнения и модели, основанные на физических принципах, чтобы предсказывать поведение атмосферы, океана и других факторов, влияющих на погоду и климат. Эти модели позволяют нам проводить эксперименты и исследования, а также прогнозировать долгосрочные изменения климата, такие как глобальное потепление или изменения в осадках.
Важно понимать, что точность прогнозирования погоды и климатических изменений основана на математических методах и моделях, которые являются результатом многолетних исследований и непрерывного совершенствования. Поэтому математика играет неотъемлемую роль в повседневной жизни, помогая нам планировать активности на улице, принимать решения о безопасности и эффективности различных отраслей промышленности, а также разрабатывать стратегии адаптации к изменяющимся климатическим условиям.
В результате, математика способствует нашему пониманию окружающего мира и позволяет нам сделать более информированные и устойчивые решения в отношении погоды и климата.
Криптография и безопасность данных: математика в защите информации

Криптография – это наука о методах обеспечения конфиденциальности, целостности и аутентичности информации, а защита данных – это широкий спектр мер, направленных на предотвращение несанкционированного доступа к информации и обеспечение ее конфиденциальности. В обоих случаях математика играет ключевую роль в разработке и анализе криптографических алгоритмов, которые обеспечивают безопасность данных.
Математические алгоритмы и методы используются для шифрования данных, что позволяет передавать информацию по открытым каналам связи, таким как интернет, с минимальными рисками несанкционированного доступа к ней. Ключи, которые используются для шифрования и расшифрования данных, также создаются и управляются с помощью математических принципов.
Другой важным аспектом криптографии является цифровая подпись, которая позволяет проверить подлинность передаваемой информации и обеспечить ее целостность.
Создание криптографических алгоритмов и протоколов требует глубоких знаний математики, включая теорию чисел, дискретную математику, линейную алгебру и математическую статистику. Математическое обоснование криптографических методов позволяет оценивать их стойкость и надежность, а также разрабатывать новые алгоритмы в ответ на появляющиеся угрозы безопасности данных.
Таким образом, математика является неотъемлемой частью криптографии и защиты данных, обеспечивая надежность и конфиденциальность передаваемой информации в нашем современном цифровом мире.
Вопрос-ответ

Какие области повседневной жизни требуют применения математики?
Математика используется во многих областях повседневной жизни. Например, она необходима при расчете бюджета, планировании времени, покупке товаров в магазине, определении дистанции и времени путешествия, приготовлении пищи и многих других ситуациях.
Как математика помогает в финансовых вопросах?
Математика играет важную роль в финансовой сфере повседневной жизни. Она помогает в рассчете процентов по ссудам и депозитам, определении налогов и страховых выплат, планировании инвестиций, управлении личными финансами и т.д. Без математических навыков было бы сложно принимать рациональные финансовые решения.
Как математика применяется в строительстве и дизайне?
В строительстве и дизайне математика используется для расчета площади и объема помещений, определения размеров и пропорций объектов, размещения мебели и элементов интерьера, создания планов зданий и многое другое. Без математических знаний было бы очень сложно создать сбалансированную и эстетически приятную архитектурную или дизайнерскую конструкцию.
В чем роль математики в нашей цифровой жизни?
Математика играет важную роль в нашей цифровой жизни. Она используется в алгоритмах поисковых систем, шифровании данных, разработке программного обеспечения, оптимизации сетей связи, создании компьютерных графиков и многих других сферах. Без математических концепций и методов не было бы возможности развития современных информационных технологий.



