В мире геометрии есть нечто особенное в форме трех сторон, но никто никогда не говорит, насколько это увлекательно! Это именно то, что позволяет нам изучать и предсказывать различные аспекты нашей физической реальности. Мы с вами сегодня поговорим о площади треугольников, но необычным и нестандартным подходом, который раскроет перед нами новые горизонты и заставит задуматься о том, какие бесконечные возможности заложены в этой простой геометрической фигуре.
Каждый из нас в школьные годы сталкивался с этим понятием, но редко кто думал о его красоте и значимости. Ведь площадь треугольника - это не просто набор цифр, вычисляемых по определенным формулам. Она воплощает в себе глубокие законы природы и гармонию форм. И сегодня мы расширим наши горизонты, разберемся в методах расчета и узнаем, почему площадь треугольника может оказаться гораздо более интересной, чем вы могли представить.
Вперед, друзья, в увлекательное путешествие, чтобы узреть магию треугольников и понять, как можно выявить ее величие через наше с вами понимание площади! Неважно, как далеко вы продвинулись в изучении математики - этот уникальный путь откроет вам новые горизонты и покажет, что треугольник скрывает в себе гораздо больше, чем могут сказать сухие формулы и определения.
Метрика фигур с равными сторонами

Для вычисления площади такого треугольника можно использовать уже известные способы, однако существует и простой и эффективный способ, который позволяет получить результат без необходимости проводить сложные вычисления.
- Первый способ:
- Найдите длину одной стороны треугольника с равными сторонами.
- Возведите найденную длину в квадрат.
- Умножьте полученное значение на корень из трех и поделите на 4.
- Измерьте длину любой из сторон треугольника с равными сторонами.
- Возведите найденную длину в квадрат.
- Поделите полученное значение на 4.
- Умножьте полученный результат на корень из трех.
Эти простые методы позволяют быстро вычислить площадь равностороннего треугольника и достаточно точно оценить его размеры, даже без использования подробных математических расчетов.
Определение площади треугольника
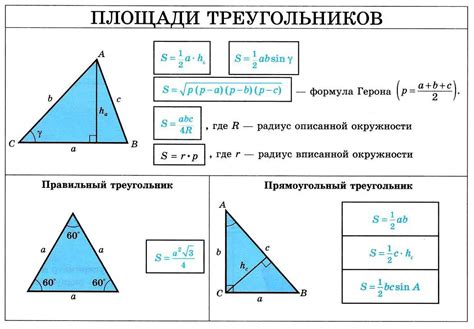
Данное разделение представляет собой описание процесса определения площади треугольника, используя различные методы и формулы.
Изучение размеров плоских фигур является важным в математике и имеет применение в различных областях, начиная от геометрии до инженерии. Определение площади треугольника является одной из основных задач, поскольку треугольники являются простейшими многоугольниками.
Определение площади треугольника может быть выполнено с использованием различных методов. Один из них - это использование формулы Герона, основанной на длинах сторон треугольника. Второй метод, который может быть применен, основан на использовании высоты треугольника. В каждом из этих методов есть свои преимущества и условия применения.
Важно отметить, что эффективность каждого метода зависит от доступной информации о треугольнике, например, известных значений сторон или высоты.
Определение площади треугольника является важным шагом для решения различных задач и может быть выполнено с помощью одного из методов, учитывая имеющуюся информацию о треугольнике.
Простой метод вычисления площади треугольника с использованием формулы Герона
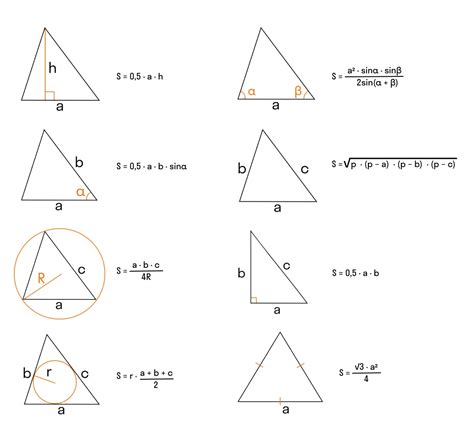
Расчет площади треугольника может быть выполнен с помощью простого и эффективного метода, основанного на формуле Герона. Данный метод позволяет получить точное значение площади треугольника, исходя из длин его сторон, без необходимости знания высоты или углов треугольника.
Формула Герона определяет, что площадь треугольника вычисляется как квадратный корень из произведения полупериметра треугольника и разностей полупериметра и длин его сторон:
| Формула Герона |
|---|
| S = √(p(p-a)(p-b)(p-c)) |
Где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c)/2), а a, b, c - длины сторон треугольника.
Этот метод является удобным для использования, так как требует всего лишь знания длин сторон треугольника и простой математической операции. Предлагаем вам попробовать использовать данный метод для расчета площади треугольников с разными сторонами и оценить его эффективность и точность.
Расчет площади треугольника при помощи полупериметра
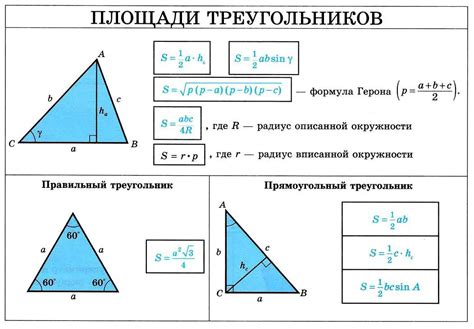
В данном разделе мы рассмотрим один из методов расчета площади треугольника, основанный на использовании полупериметра. Здесь мы избегаем директных определений и приводим общую идею данного подхода к расчету площади треугольника.
Работа с примерами: пошаговое вычисление площади треугольника
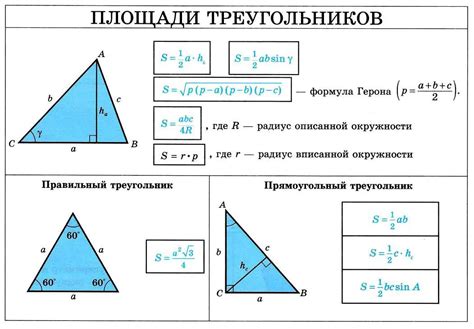
В этом разделе мы рассмотрим несколько примеров и шаг за шагом научимся находить площадь треугольника. Мы будем использовать альтернативные термины, чтобы разнообразить текст и избежать повторений.
Давайте начнем с первого примера, в котором у нас есть треугольник с заданными сторонами. Наша задача - вычислить площадь этого треугольника, используя доступную информацию. Мы применим некоторые основные формулы и методы для достижения этой цели.
Также мы рассмотрим пример с заданными значениями высоты и основанием треугольника. Мы узнаем, как эти значения могут помочь нам определить площадь треугольника и какие шаги нам необходимо предпринять для ее вычисления.
В следующем примере мы рассмотрим ситуацию, когда нам даны координаты вершин треугольника на плоскости. Мы узнаем, как применить формулу для расчета площади треугольника по координатам вершин и какие шаги важно выполнить для достижения желаемого результата.
Каждый из этих примеров поможет вам понять, как найти площадь треугольника, начиная с различных входных данных. Следуя нашим подробным инструкциям, вы сможете легко вычислить площадь треугольника, даже если у вас нет точных значений его сторон.
Упражнения для развития навыков вычисления площади треугольника
Раздел "Упражнения для тренировки нахождения площади треугольника" предлагает набор задач, которые помогут вам развить навыки вычисления площади треугольников без использования специальных формул или заданных размеров сторон. В отличие от простых расчетов площади, эти упражнения требуют от вас творческого мышления и способности абстрагироваться от конкретных данных.
В процессе выполнения задач вы будете использовать общие понятия треугольника и связанные с ним свойства, чтобы сформулировать и решить каждую задачу. Этот тип упражнений развивает не только навык вычисления площади треугольников, но и способность анализировать ситуацию, применять логику и принимать обоснованные решения.
- Упражнение 1: Поиск площади подобного треугольника
- Упражнение 2: Построение треугольника с заданной площадью
- Упражнение 3: Разделение треугольника на более мелкие фигуры
- Упражнение 4: Площадь треугольника через высоту и основание
- Упражнение 5: Расчет площади треугольника по известным углам
Каждое упражнение предлагает уникальный подход к вычислению площади треугольника и предоставляет возможность попрактиковаться в использовании разных методов и приемов. Выполняя данные задачи, вы будете тренировать свое интуитивное понимание геометрии и углубленное понимание свойств треугольников.
Запаситесь карандашом, бумагой и готовьтесь к захватывающим головоломкам! Упражнения для тренировки нахождения площади треугольника помогут вам стать настоящим экспертом в геометрии и открыть новые способы подхода к решению задач.
Приложения изучения площади треугольника в реальных ситуациях

1. Землеустройство: Понимание площади треугольника является неотъемлемой частью землеустройства. Земельные участки, границы и земельные карты определяются с использованием треугольников, и знание площади и их геометрических свойств помогает с определением размеров и координат местоположения.
2. Инженерное строительство: Площадь треугольника полезна для инженеров при проектировании и строительстве различных сооружений. Расчет площади позволяет определить необходимое количество материалов, таких как кирпич, бетон или плиты для строительства фундамента, стен или крыши.
3. Навигация: Определение площади треугольника может быть полезно в навигации и ориентации в пространстве. Например, при навигации по морю или воздуху, зная площадь треугольника, можно определить площади зоны видимости для ориентации и планирования пути.
4. Дизайн интерьера: В области дизайна интерьера, знание площади треугольника помогает в планировании расположения мебели и декоративных элементов. Правильное использование пространства требует учета площади и симметрии треугольников для создания гармоничного дизайна.
Понимание и применение площади треугольника играют важную роль в различных сферах жизни. От архитектуры до землеустройства, от инженерии до дизайна, наше умение расчитывать площадь треугольника помогает нам эффективно и точно решать задачи в реальном мире.
Вопрос-ответ

Как найти площадь треугольника?
Для расчета площади треугольника, нужно знать длины его сторон и применить формулу Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь, p - полупериметр треугольника, a, b, c - длины сторон.
Как использовать формулу Герона для нахождения площади треугольника?
Для этого нужно найти полупериметр треугольника, сложив длины всех его сторон и поделив на 2. Затем, подставить найденные значения в формулу S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь, p - полупериметр, a, b, c - длины сторон.
Как найти площадь треугольника, если известны только длины его сторон?
Если известны только длины сторон треугольника, то можно воспользоваться формулой Герона. Найдите полупериметр треугольника, то есть сложите длины всех его сторон и разделите на 2. Затем, подставьте найденные значения в формулу S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь, p - полупериметр, a, b, c - длины сторон.
Можно ли найти площадь треугольника, зная только его высоту?
Да, можно. Если известна высота треугольника, то площадь можно найти по формуле S = (a * h) / 2, где S - площадь, a - длина основания треугольника, h - высота треугольника.
Можно ли найти площадь треугольника, если неизвестны длины его сторон?
Нет, без информации о длинах сторон треугольника нельзя точно найти его площадь. Для расчета площади треугольника необходимы длины его сторон, либо длина основания и высота. Исходя из этих данных, можно использовать соответствующие формулы для нахождения площади треугольника.