Как определить высоту треугольника по известной основе - простые шаги для измерения и исследования

В изучении геометрии треугольники занимают особое место. Мы сталкиваемся с ними повсюду: в строительстве, инженерии, архитектуре и даже в кулинарии. Знание высоты треугольника является важным элементом для решения таких задач, как определение площади или нахождение других сторон. В этой статье мы рассмотрим способы определения высоты треугольника, пользуясь лишь информацией о его одной стороне.

Высота треугольника – это отрезок, проведенный из вершины до противоположной стороны и перпендикулярный ей. Проблема заключается в том, что высота треугольника не всегда является известной величиной. Во многих задачах мы имеем информацию только о его сторонах или углах. К счастью, существуют способы определить высоту треугольника, используя лишь одну из его сторон и дополнительные геометрические свойства.

Определение высоты треугольника может быть осуществлено с помощью различных методов и формул. Некоторые из них требуют использования треугольника Пифагора или подобных треугольников, другие опираются на теорему синусов или теорему косинусов. Для простоты мы рассмотрим наиболее распространенный метод – использование площади треугольника.

Основная концепция определения высоты треугольника

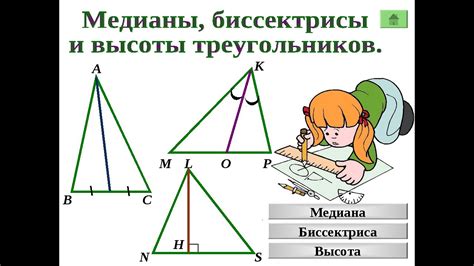
Теорема углового подобия: При рассмотрении прямолинейных треугольников можно использовать пропорции между сторонами и высотами, чтобы определить высоту треугольника. Данная теорема основана на свойствах радиусов и тангенса углов и поможет нам найти высоту треугольника с помощью уже имеющихся данных о его сторонах и диагоналях.
Теорема Пифагора: Применение этой теоремы позволяет нам определить высоту треугольника, когда даны его катеты. Зная длины катетов треугольника и применяя теорему Пифагора, мы можем вычислить длину гипотенузы и применить полученные данные для определения высоты.
Метод синусов: Обратившись к теореме синусов, мы можем определить высоту треугольника, если известны длины его сторон и углы. Применение данной теоремы позволит нам вычислить высоту треугольника, используя соотношения между сторонами и синусами соответствующих углов.

Использование этих основных принципов позволяет определить высоту треугольника без необходимости измерений и обеспечивает более гибкое и универсальное решение этой задачи.

Формула для вычисления площади треугольника при известной основе и высоте

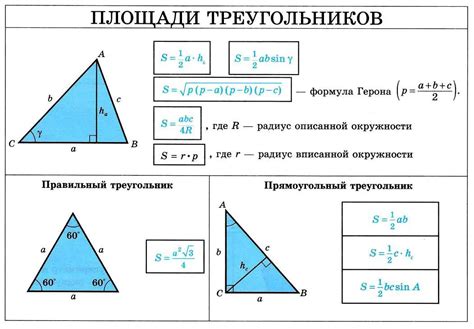
Установить площадь треугольника можно с помощью формулы, которая основана на известной длине основы и высоте данной фигуры. Расчет площади треугольника представляет собой важную задачу в геометрии, позволяющую определить площадь треугольника без знания дополнительных параметров.

Для начала необходимо определить, что основа треугольника является одной из его сторон, относительно которой рассчитывается его высота. Высота треугольника - это отрезок, опускаемый из вершины фигуры на ее основание под прямым углом.

Формула для вычисления площади треугольника при известной основе и высоте выглядит следующим образом:

Площадь = (Основа * Высота) / 2

Здесь "Основа" представляет собой длину основания треугольника, а "Высота" обозначает его высоту, построенную на это основание. Для применения данной формулы необходимо знать значения основы и высоты треугольника.

Таким образом, нахождение площади треугольника по известной основе и высоте может быть осуществлено с использованием простой математической формулы, которая позволяет установить площадь фигуры, основываясь только на основе и высоте треугольника.

Методы вычисления высоты треугольника при неизвестной площади

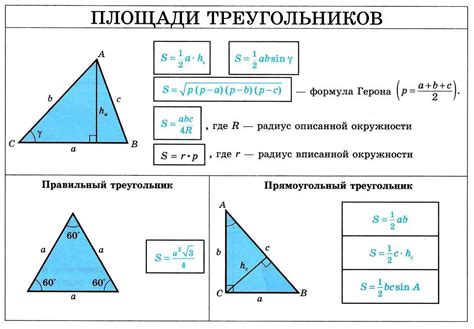
Найдение высоты треугольника может быть сложной задачей, особенно когда площадь треугольника неизвестна. Однако, существуют различные методы, которые позволяют определить высоту треугольника, даже когда основные параметры неизвестны.

1. Использование подобия треугольников: одним из способов определения высоты треугольника без информации о его площади является использование подобия треугольников. При условии, что треугольник задан своей основой и углами, можно найти подобный треугольник с известной площадью и применить свойства подобных треугольников для определения высоты.

2. Использование формулы герона: формула герона позволяет вычислить площадь треугольника по длинам его сторон. Если известны длины всех сторон треугольника, можно использовать формулу герона для нахождения площади и затем применить соответствующий метод для определения высоты.

3. Использование теоремы Пифагора: в некоторых случаях, когда треугольник является прямоугольным, можно применить теорему Пифагора для определения длины неизвестной стороны. Затем, имея информацию о длине основы треугольника, можно вычислить площадь и, в конечном итоге, определить высоту.

Использование этих методов позволяет определить высоту треугольника, не зная его площадь. Однако, для более точного определения высоты рекомендуется иметь как можно больше известных параметров треугольника.

Использование Теоремы Пифагора для расчета высоты треугольника

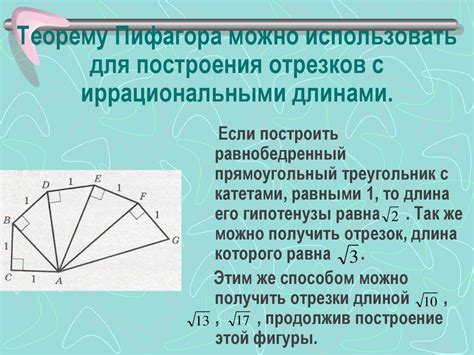
В данном разделе мы рассмотрим метод, основанный на использовании знаменитой Теоремы Пифагора, который позволяет нам определить высоту треугольника. Применение этого подхода позволяет нам расчетать длину высоты треугольника, необходимую для решения различных геометрических задач.

В качестве отправной точки используем известную основу треугольника, анализируя ее длину и соотношения между сторонами треугольника. С использованием Теоремы Пифагора, мы можем вывести формулу, которая позволяет нам вычислить длину высоты треугольника, используя известные данные. Формула основана на применении теоремы Пифагора к одной из боковых сторон треугольника.

Для использования этого метода необходимо знать длину основы треугольника и его боковых сторон. Затем мы можем использовать формулу, чтобы определить третью сторону треугольника, неизвестную нам. После этого, применяя Теорему Пифагора, мы можем рассчитать длину высоты треугольника. Этот метод может быть полезен в различных задачах, связанных с определением высоты треугольника, как в геометрических расчетах, так и в практических применениях.

Шаг 1: Известная основа треугольника
Шаг 2: Измерение боковых сторон треугольника
Шаг 3: Вычисление третьей стороны треугольника
Шаг 4: Применение Теоремы Пифагора для определения высоты треугольника

Использование Теоремы Пифагора для определения высоты треугольника является эффективным и универсальным методом, который может быть применен в различных ситуациях. Этот подход позволяет нам получить значение высоты треугольника, используя информацию о его основе и боковых сторонах. Он предоставляет нам удобный инструмент для решения задач геометрии и дает возможность проводить точные расчеты в различных областях, требующих определения высоты треугольника.

Геометрический подход к определению высоты треугольника

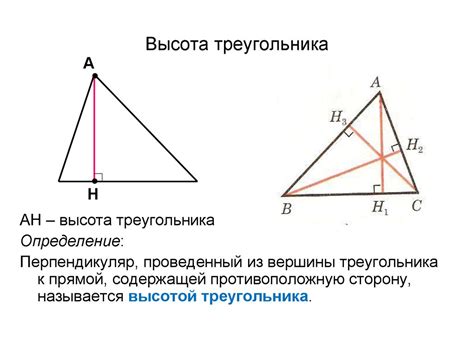
Геометрический способ нахождения высоты треугольника представляет собой уникальный подход к определению этого параметра, используя информацию о длине основы и геометрические свойства треугольника. С помощью этого метода можно точно определить высоту треугольника, не зная значения углов или длины других сторон.

Для проведения геометрического подсчета высоты треугольника, исходя из заданной основы, необходимо воспользоваться одним из свойств треугольника. Например, одной из наиболее распространенных теорем, используемых для этого, является теорема Пифагора. Эта теорема основывается на связи между сторонами прямоугольного треугольника и может быть применима в различных случаях.

Применимость этой теоремы в нахождении высоты треугольника основана на его свойствах, в частности на том, что высота, опущенная на основу, является перпендикуляром к этой основе. Поэтому, зная длину основы и одну из других сторон треугольника, можно использовать теорему Пифагора для определения высоты.

В применении геометрического подхода определения высоты треугольника важно учитывать углы и стороны треугольника, чтобы использовать соответствующие свойства и формулы. Например, в случае равнобедренного треугольника имеется дополнительное свойство, когда высота, опущенная от вершины до основания, является биссектрисой треугольника. Это свойство можно использовать для нахождения высоты с помощью геометрических выкладок и формул, основанных на углах и сторонах треугольника.

Практическое применение вертикали треугольника

Практическое использование в архитектуре и строительстве: зная высоту треугольника, можно определить длину лестницы, необходимую для достижения определенной высоты здания. Также, для расчета конструкций в зданиях, архитекторы и инженеры используют высоту треугольника как основной параметр.
Применение в геодезии и картографии: определение высоты треугольника помогает специалистам определять высоту зданий, гор и других объектов по известной основе. Это необходимо для составления точных карт и географических планов.
Использование в физике: высота треугольника играет важную роль в законе Архимеда для определения объема тела, погруженного в жидкость или газ. Этот принцип находит свое применение в расчетах плавучести и взаимодействия тел с жидкостью.
Применение в геометрии и математике: высота треугольника служит ключевым инструментом для решения различных геометрических задач, таких как нахождение площадей и объемов, вычисление длин сторон и углов треугольника, а также определение свойств треугольника в общем.
Применение в аэронавтике и навигации: в определении высоты самолетов, ракет и спутников используется принцип треугольника и известная основа. Это помогает определить точное положение объекта в пространстве и правильно учитывать его относительное положение к поверхности Земли.

Способы измерения высоты треугольника в реальных условиях

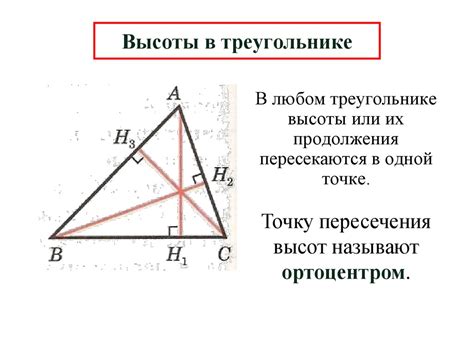
В реальных условиях, когда нет возможности использовать математические формулы и точные измерения, существуют различные способы определения высоты треугольника по заданной основе. Рассмотрим несколько методов, которые могут быть полезными при решении данной задачи.

1. Использование теодолита:

Определение точки на основе треугольника, от которой будет проводиться вертикальная линия;
Установка теодолита так, чтобы он был направлен на выбранную точку;
Измерение угла наклона теодолита и вычисление высоты треугольника с помощью геометрических формул.

2. Метод с использованием угломера:

Установка угломера на основе треугольника, направленного на землю;
Измерение углов между горизонтом и отрезками, соединяющими вершины треугольника с точкой, от которой будет проводиться вертикальная линия;
Вычисление высоты треугольника с использованием геометрических формул.

3. Визуальный метод с использованием уровня:

Установка уровня на основе треугольника так, чтобы он был параллелен земле;
Определение точки на основе треугольника, от которой будет проводиться вертикальная линия;
Определение отклонения уровня от горизонтального положения и вычисление высоты треугольника с помощью геометрических формул.

Каждый из этих методов имеет свои преимущества и ограничения, и выбор конкретного способа зависит от доступных инструментов и условий проведения измерений. Независимо от выбранного метода, важно учитывать точность измерений и возможные погрешности, чтобы получить наиболее достоверный результат.

Задачи на нахождение высоты треугольника в геометрии

Одной из таких задач является нахождение высоты треугольника на основе его сторон. Предположим, что у нас есть треугольник с известными значениями длин его сторон. Необходимо определить высоту этого треугольника. В данной задаче мы рассмотрим разные методы, с помощью которых можно найти высоту треугольника и описать их применение.

Другой интересной задачей является определение высоты треугольника на основе его площади и одной из сторон. В данном случае, известны площадь треугольника и длина одной из его сторон, и требуется найти высоту. Мы рассмотрим различные подходы к решению этой задачи и изучим их особенности.

Кроме того, существуют и другие задачи, где требуется определить высоту треугольника на основе различных данных, таких как углы треугольника или радиус вписанной окружности. Мы рассмотрим такие случаи и рассмотрим их решения.

Расчеты с использованием тригонометрии для определения высоты треугольника

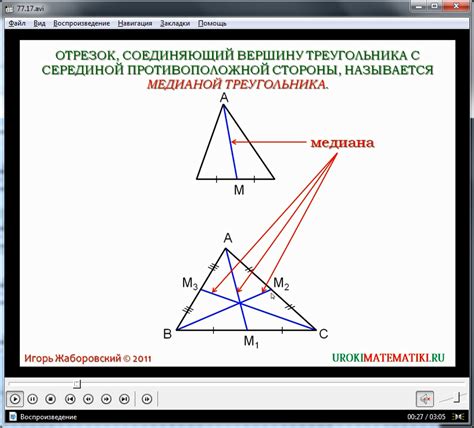
В данном разделе мы рассмотрим методы расчета высоты треугольника с использованием тригонометрических функций. С помощью этих методов можно определить вертикальное расстояние от одной вершины треугольника до противолежащей стороны.

Применение теоремы синусов:

Первый способ позволяет определить высоту треугольника, если известны длина основы и соответствующий угол.

Для начала, найдем синус данного угла, разделив противолежащую сторону на гипотенузу. Затем, умножим полученное значение на длину основы, чтобы получить высоту треугольника.

Формула для расчета высоты треугольника:

h = a * sin(α)

Где h - высота треугольника, a - длина основы, α - угол между основой и противолежащей стороной.

Применение теоремы косинусов:

Второй способ использует теорему косинусов для определения высоты треугольника при известных длинах всех сторон.

Для начала, найдем косинус угла, образованного противолежащей стороной и основой. Затем, умножим полученное значение на длину основы, чтобы найти высоту треугольника.

Формула для расчета высоты треугольника:

h = a * cos(β)

Где h - высота треугольника, a - длина основы, β - угол между основой и противолежащей стороной.

Используя эти методы расчета высоты треугольника, вы сможете более точно определить его геометрические параметры и применить полученные данные в различных математических и физических задачах.

Вопрос-ответ