Необходимо осмыслить и понять, как изменяются значения определенных функций при изменении угла в системе координат. Это позволит более глубоко понять связь между геометрическим представлением и математическими выражениями.
В данном разделе мы предлагаем рассмотреть зависимости между углами и функциями, которые могут быть представлены графически и аналитически. У нас есть возможность исследовать функции, определенные на единичном круге и понять, как они изменяются, когда угол меняется от 0 до 360 градусов.
Основные понятия и свойства окружности
Основное понятие, характеризующее окружность, - это ее радиус. Радиус определяется как расстояние от центра окружности до любой ее точки. Фактически, радиус является элементарным строительным блоком для определения других важных величин, связанных с окружностью.
Другая значимая характеристика окружности - ее диаметр. Диаметром окружности называется отрезок, соединяющий две противоположные точки на окружности и проходящий через ее центр. Диаметр является в два раза больше радиуса и служит для задания масштаба окружности.
Важной концепцией, связанной с окружностью, является окружной угол. Окружным углом называется угол между двумя лучами, имеющими общую начальную точку, лежащую на окружности, и точкой пересечения этих лучей, также находящейся на окружности.
Окружности обладают целым рядом свойств, которые являются основой для решения различных задач. Например, равенство длин окружностей соответствующих радиусов, равенство центральных углов окружностей с одинаковыми диаметрами, а также формула для вычисления площади круга - все эти свойства делают окружности уникальными и очень полезными объектами изучения.
Что такое круг и какие у него особенности?
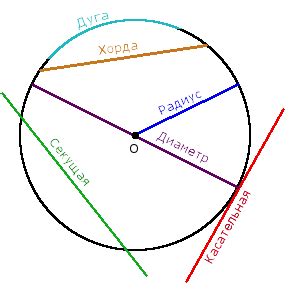
Главная характеристика окружности - это то, что она представляет собой единую замкнутую кривую линию, состоящую из точек, равноудаленных от одной фиксированной точки, называемой центром. Точки, принадлежащие окружности, называются ее точками.
Диаметр – это отрезок, соединяющий две противоположные точки на окружности и проходящий через ее центр. Длина диаметра равна удвоенному радиусу окружности.
Радиус - это отрезок, соединяющий центр окружности с ее точкой. Радиус является основным показателем размера окружности.
Окружность имеет множество свойств и характеристик:
- Периметр окружности равен удвоенному произведению числа π (пи) на радиус окружности.
- Площадь окружности равна произведению числа π (пи) на квадрат радиуса окружности.
- Всякая окружность однозначно задается своим радиусом.
- Если две окружности имеют одинаковые радиусы, то они считаются равными между собой.
- На окружности можно определить дуги – части окружности между двумя ее точками.
- Хорда – отрезок, соединяющий две точки на окружности.
Знание свойств и особенностей окружности, а также умение работать с ними, являются важными и необходимыми величинами при изучении и использовании геометрии, физики, инженерных и научных расчетов.
Тригонометрические функции и геометрические свойства на окружности
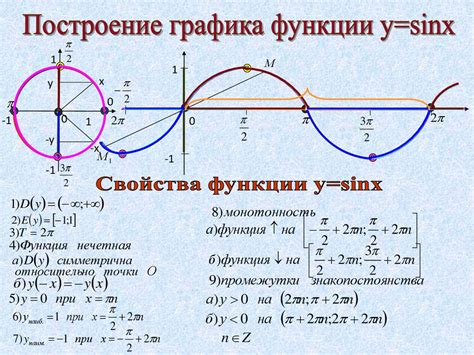
В данном разделе представлены основные идеи и свойства тригонометрических функций, которые находят свое применение в геометрии окружности. Здесь мы исследуем взаимосвязь между углами, радиусами и длинами дуг на окружности, а также их соотношение с синусом и косинусом.
Используя геометрические инструменты, такие как таблицы и измерения, мы сможем показать, как тригонометрические функции связаны с геометрическими характеристиками окружности, такими как радиус и длина дуги. Мы рассмотрим свойства синуса и косинуса и их отношение к движению точки на окружности.
| Угол | Синус | Косинус |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 1/2 | √3/2 |
| 45° | √2/2 | √2/2 |
| 60° | √3/2 | 1/2 |
| 90° | 1 | 0 |
Также мы рассмотрим правила нахождения значений синуса и косинуса для углов больше 90°, используя примеры на окружности. Это поможет нам полностью понять, как тригонометрические функции работают и применяются в геометрии.
Исследование этих тем и свойств тригонометрических функций на окружности поможет нам лучше понять и использовать их в контексте геометрических задач и вычислений.
Что такое синус и косинус и каковы их характеристики?
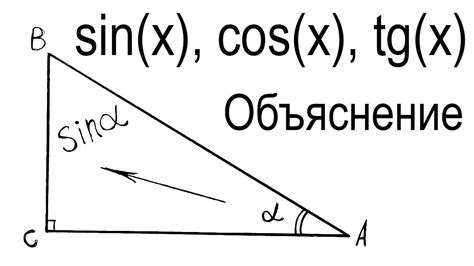
Синус можно рассматривать как характеристику объекта, отображающую его высоту или расстояние от некоторой базовой линии. Косинус, с другой стороны, является показателем горизонтальной составляющей объекта относительно этой базовой линии.
Оба этих понятия имеют ряд важных свойств, которые делают их полезными в различных областях. Например, синус и косинус являются периодическими функциями, что означает, что их значения повторяются через регулярные интервалы. Они также являются непрерывными функциями, что означает, что они могут быть представлены как гладкие кривые.
Кроме того, синус и косинус являются взаимосвязанными функциями, а именно, они связаны между собой формулой Пифагора: синус в квадрате плюс косинус в квадрате равны единице. Это свойство позволяет нам использовать эти функции для вычисления и анализа друг друга.
Синус и косинус также играют важную роль в геометрии, особенно в отношении окружностей. Они позволяют нам определить положение точек на окружности и вычислить углы между различными линиями и поверхностями.
Таким образом, синус и косинус представляют собой мощные и многофункциональные математические инструменты, которые помогают нам лучше понимать и описывать мир вокруг нас. Их свойства и возможности чрезвычайно широки и находят применение в различных научных и практических областях, от физики и инженерии до компьютерной графики и статистики.
Как получить значения тригонометрических функций при работе с углами на окружности?

Для решения различных задач, связанных с углами на окружности, необходимо иметь навыки определения значений синуса и косинуса. Вместо прямого упоминания этих функций, мы будем искать способы расчета вспомогательных величин, позволяющих нам получить значения синонимов этих функций.
Один из подходов к решению этой задачи - использование отношений между сторонами треугольников, образованных при соединении точек окружности с началом координат и точкой на окружности.
Важно отметить, что значение синуса угла на окружности всегда будет находиться в диапазоне от -1 до 1, а значение косинуса - также в диапазоне от -1 до 1.
Таким образом, при изучении и применении тригонометрических функций при работе с углами на окружности, необходимо уметь определять соответствующие значения, используя вспомогательные величины и отношения между ними.
Геометрическое и тригонометрическое представление синуса и косинуса

Этот раздел посвящен геометрическому и тригонометрическому представлению синуса и косинуса. Здесь мы рассмотрим связь между этими тригонометрическими функциями и геометрическими объектами, а также способы их определения без использования прямых определений.
- Геометрическое представление
- Тригонометрическое представление
- Связь между геометрическим и тригонометрическим представлением
Первый способ представления синуса и косинуса основан на геометрическом представлении окружности и треугольника. Мы рассмотрим связь между этими функциями и радиусом окружности, а также показатели и углы между радиусом и прямой, проходящей через конец радиуса и центр окружности.
Второй способ представления синуса и косинуса основан на использовании тригонометрических функций и отношений между сторонами треугольника. Мы изучим основные тригонометрические соотношения и формулы, позволяющие определить эти функции для различных углов и треугольников.
В заключительной части раздела мы рассмотрим связь между геометрическим и тригонометрическим представлением синуса и косинуса. Будет рассмотрен подход, позволяющий использовать геометрические концепции для дальнейшего изучения свойств и применений этих тригонометрических функций.
Представление синуса и косинуса угла в геометрическом и тригонометрическом виде

Рассмотрим способы представления синуса и косинуса угла, которые возникают при изучении геометрии и тригонометрии. В геометрическом виде синус и косинус угла можно представить с помощью геометрических фигур, таких как треугольник или единичная окружность. Тригонометрическое представление синуса и косинуса угла основано на отношении сторон треугольника и часто используется в решении задач связанных с расчетами с данными функциями.
При использовании геометрического представления синус и косинус угла могут быть выражены отношениями сторон треугольника. Синус угла равен отношению противолежащего катета и гипотенузы, а косинус угла равен отношению прилежащего катета и гипотенузы. Это геометрическое понимание синуса и косинуса позволяет визуализировать эти функции, особенно при решении задач, связанных с треугольниками и их свойствами.
В тригонометрическом представлении синус и косинус угла представлены с помощью величин, зависящих только от значения угла. Синус угла определяется как отношение противолежащего катета к гипотенузе, а косинус угла - как отношение прилежащего катета к гипотенузе. В отличие от геометрического представления, тригонометрическое представление позволяет работать с функциями синуса и косинуса независимо от конкретных геометрических фигур, что делает их удобными для математических вычислений и анализа.
- Геометрическое представление синуса и косинуса угла основано на отношениях сторон треугольника.
- Тригонометрическое представление синуса и косинуса угла выражается величинами, зависящими только от значения угла.
- Понимание и использование обоих способов представления синуса и косинуса позволяет решать разнообразные задачи, связанные с геометрией и тригонометрией.
Вопрос-ответ

Как можно найти синус и косинус на окружности?
Чтобы найти синус и косинус на окружности, нужно использовать геометрические свойства треугольника. Для этого можно взять произвольную точку на окружности и построить прямые линии, соединяющие эту точку с началом координат и вершиной окружности. Длина горизонтального отрезка, соединяющего начало координат с вершиной, будет равна косинусу угла, а длина вертикального отрезка будет равна синусу угла.
Какой угол соответствует синусу или косинусу на окружности?
Угол, соответствующий синусу или косинусу на окружности, зависит от выбранной точки на окружности и начала координат. Если мы берем точку на окружности, соединяем ее с началом координат и вершиной окружности, то угол, образуемый горизонтальной осью и этим отрезком, будет соответствовать косинусу. В то же время, угол между вертикальной осью и этим отрезком будет соответствовать синусу.
Какое значение может иметь синус или косинус на окружности?
Значение синуса и косинуса на окружности может изменяться в пределах от -1 до 1. Это связано с тем, что длины отрезков, соответствующих синусу и косинусу, всегда меньше радиуса окружности, а радиус окружности равен 1. Таким образом, синус и косинус могут принимать любые значения от -1 до 1 включительно.
Как можно использовать значения синуса и косинуса на окружности в математике?
Значения синуса и косинуса на окружности широко используются в математике и физике. Они помогают в решении уравнений, изучении периодических функций, нахождении амплитуды и фазы колебаний, а также во многих других областях. Эти значения также используются в построении графиков тригонометрических функций.
Как можно найти значения синуса и косинуса на окружности?
Чтобы найти значения синуса и косинуса на окружности, необходимо использовать координаты точки на окружности. Для этого можно воспользоваться тригонометрическим кругом и теоремой Пифагора.



