Все мы обращали внимание на то, что окружность - это одно из основных понятий геометрии. Эта геометрическая фигура, не имеющая начала и конца, обладает множеством удивительных свойств, которые привлекают внимание учёных и любознательных исследователей. Однако, не всегда нам нужно изучать идеальные окружности в их полном виде. Иногда нам нужно найти только часть окружности, и делать это может быть не так уж и просто.
Что же делать в таких ситуациях? Каким образом мы можем посчитать длину сегмента окружности, зная только его диаметр? Оказывается, существуют простые шаги и формулы, которые помогут нам справиться с этой задачей. В данной статье мы поговорим о том, каким образом можно вычислить длину сегмента окружности при известном диаметре, не прибегая к сложным математическим выкладкам.
Сначала давайте разберёмся, что такое сегмент окружности. Это часть плоскости, которая ограничена окружностью и дугой, соединяющей две точки на окружности. Сегмент окружности может быть как маленьким и почти равным дуге, так и большим и охватывающим практически половину окружности.
Длина окружности: от диаметра к границам
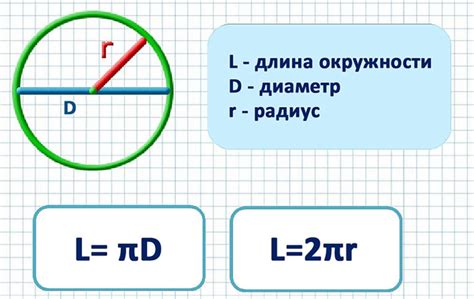
Для вычисления длины окружности мы можем использовать знакомую формулу: "длина окружности равна произведению диаметра на число π". Данный подход позволяет найти точное значение длины окружности и использовать его в дальнейших расчетах.
Однако, если нам требуется приближенное значение, можно воспользоваться аппроксимацией, сокращая значение числа π до простого десятичного числа. Это позволяет снизить сложность вычислений и упростить дальнейшие расчеты в различных сферах деятельности.
Итак, чтобы найти длину окружности, вам нужно записать формулу: L = πd, где L обозначает длину окружности, а d - диаметр. Затем вычислите произведение числа π на заданный диаметр и получите точное или приближенное значение длины окружности в зависимости от ваших целей.
Простые инструкции для расчета площади круга c помощью диаметра
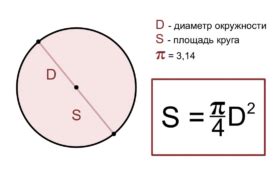
В этом разделе мы рассмотрим простые шаги для определения площади круга на основе известного значения его диаметра. При помощи нескольких математических формул и конкретных алгоритмов вы сможете рассчитать площадь круга без особых трудностей.
- Измерьте диаметр круга: данный параметр представляет собой прямую линию, проходящую через центр круга и имеющую две равные части.
- Найдите радиус круга: радиус - это половина диаметра и обозначает расстояние от центра круга до его любой точки.
- Воспользуйтесь формулой площади круга: площадь круга можно рассчитать по формуле S = π * r², где π (пи) приблизительно равно 3,14, а r обозначает радиус.
- Умножьте полученное значение площади на π (пи): согласно формуле, для нахождения площади круга, нужно умножить полученную площадь на значение числа π, приблизительно равного 3,14.
После выполнения этих простых шагов вы получите точное значение площади круга на основе известного диаметра. Запомните, что диаметр является ключевым параметром для расчета площади круга, поскольку он определяет его размеры и форму.
Расчет доли окружности при заданном диаметре

Перейдем к вычислениям. Для начала, рассмотрим формулу для нахождения длины окружности, которая определяется следующим образом:
- Диаметр окружности обозначим за D.
- Найдем радиус окружности по формуле R = D/2.
- Длина окружности определяется по формуле L = 2πR, где π - математическая константа, примерно равная 3.14159.
Теперь, чтобы найти долю окружности, нам нужно знать, какую часть от общей длины окружности мы хотим найти. Эту часть обозначим за P в процентах. Для вычисления формулы необходимо выполнить следующие действия:
- Переведем проценты в десятичную дробь, разделив значение P на 100.
- Вычислим длину дуги окружности по формуле A = (P/100) * L.
- Таким образом, мы получим длину дуги окружности, которая является заданной частью от всей окружности.
Эта формула позволяет точно определить долю окружности при известном диаметре и заданной величине в процентах. Учтите, что полученная длина дуги окружности может быть выражена в любых единицах измерения, в которых измеряется длина диаметра и радиуса окружности.
Применение формулы для вычисления длины дуги окружности: руководство шаг за шагом
Шаг 1: Определите известные параметры: радиус и центральный угол
Прежде чем мы сможем приступить к использованию формулы для расчета длины дуги окружности, нам необходимо знать два основных параметра: радиус окружности и центральный угол, образуемый этой дугой. Радиус - это расстояние от центра окружности до ее любой точки, а центральный угол - это угол, измеряемый в радианах, между начальной и конечной точками дуги.
Шаг 2: Примените формулу для вычисления длины дуги окружности
Теперь, когда у нас есть необходимые сведения, мы можем приступить к применению формулы для определения длины дуги окружности. Формула, используемая для вычисления, основывается на соотношении между центральным углом и полным углом окружности.
(Здесь можно упомянуть формулу длины дуги окружности на базе длины окружности)
Шаг 3: Рассчитайте и получите длину дуги окружности
Последним шагом является вычисление и окончательное получение длины дуги окружности. Просто замените известные значения радиуса и центрального угла в формулу и выполните несложные математические операции для получения точного результата.
Теперь, зная простые шаги и применяя соответствующую формулу, вы можете эффективно определить длину дуги окружности без необходимости знать ее диаметр. Этот метод является полезным инструментом не только в математике, но и в других областях, где требуется вычисление протяженности окружностей.
Вопрос-ответ

Как найти длину дуги при известном диаметре окружности?
Длина дуги окружности может быть найдена с помощью формулы: L = π * d, где L - длина дуги, π - математическая константа, приблизительно равная 3.14, d - диаметр окружности.
Как найти угол, соответствующий заданной части окружности?
Угол, соответствующий заданной части окружности, может быть найден с помощью формулы: α = 360 * (L / (π * d)), где α - угол в градусах, L - длина дуги окружности, π - математическая константа, приблизительно равная 3.14, d - диаметр окружности.
Можно ли найти часть окружности, не зная диаметр?
Да, можно найти часть окружности, не зная диаметр. Для этого необходимо знать либо длину дуги, либо центральный угол, соответствующий этой части окружности, и использовать соответствующую формулу для расчета нужного параметра.
Как найти радиус окружности, зная диаметр?
Радиус окружности может быть найден с помощью формулы: r = d / 2, где r - радиус окружности, d - диаметр окружности.
Как найти длину дуги окружности, если известен угол, соответствующий этой дуге?
Длина дуги окружности может быть найдена с помощью формулы: L = α * (π * d) / 360, где L - длина дуги, α - угол в градусах, π - математическая константа, приблизительно равная 3.14, d - диаметр окружности.
Какой диаметр окружности следует знать для расчета ее части?
Для расчета части окружности, необходимо знать ее диаметр, то есть расстояние между двумя противоположными точками на окружности, проходящими через ее центр.



