Рассмотрим одну из интересных задач геометрии, связанную с равнобедренными треугольниками. Эти треугольники, как сразу понятно из названия, имеют две равные стороны и два равных угла. В таких фигурах есть особенность, касающаяся положения основания, которая вызывает множество вопросов и требует специальных методов определения.
Необходимость определить положение основания в равнобедренном треугольнике возникает при решении различных задач геометрии, а также при проектировании и построении разных сооружений. От правильного решения этой задачи зависит точность и качество дальнейших вычислений, а также безопасность и надежность строительства.
Существуют разные методы определения положения основания в равнобедренном треугольнике, каждый из которых подходит для определенных условий и задач. Некоторые методы основаны на использовании подобия треугольников, другие позволяют рассчитать координаты основания с помощью тригонометрических функций. При выборе метода необходимо учитывать доступность и точность используемых инструментов, а также сложность и объем вычислений.
Тригонометрический метод установления местонахождения базы в треугольнике с равными боковыми сторонами
Для определения местонахождения базы применяются математические вычисления, основанные на соотношениях между углами и сторонами треугольника. При использовании тригонометрического метода необходимо учитывать сходство правильных прямоугольных треугольников, а также соотношения между площадью треугольника, его сторонами и углами.
Для определения местоположения базы в равнобедренном треугольнике можно использовать такие понятия, как синусы, косинусы и тангенсы углов треугольника. Главное преимущество тригонометрического метода заключается в его точности и возможности применения для различных типов треугольников.
Таким образом, тригонометрический метод является эффективным инструментом для определения местонахождения базы в равнобедренном треугольнике. Он позволяет с высокой точностью вычислить координаты основания, основываясь на теоремах и формулах тригонометрии и используя соотношения между углами и сторонами треугольника.
Расчет местоположения основания в равнобедренном треугольнике через теоремы синусов и косинусов
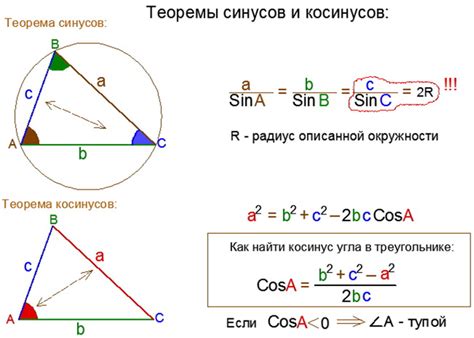
Теорема синусов устанавливает соотношение между длинами сторон треугольника и синусами соответствующих им углов. Используя эту теорему, можно вычислить длину одной из сторон равнобедренного треугольника, основываясь на известных значениях углов и длины другой стороны.
С другой стороны, теорема косинусов позволяет определить длину одной из сторон треугольника, используя длины двух других сторон и значение косинуса угла между ними. Это может быть полезно при расчете расстояния от вершины треугольника до основания.
- Используя теорему синусов, можно получить выражение для длины стороны основания треугольника через синус половины вершинного угла и длину одной из боковых сторон.
- Теорема косинусов позволяет найти горизонтальную составляющую длины стороны основания через значения косинусов углов при основании и половину угла при вершине.
- Сочетание этих двух теорем позволяет определить положение основания в равнобедренном треугольнике путем расчета длины стороны основания или расстояния от вершины треугольника до основания.
Использование теорем синусов и косинусов позволяет более точно определить местоположение основания в равнобедренном треугольнике и провести необходимые расчеты с высокой точностью.
Геометрический способ определения положения основания в равнобоком треугольнике

В данном разделе будут рассмотрены геометрические методы, позволяющие определить положение основания в равнобедренном треугольнике. Эти методы основаны на использовании свойств и геометрических закономерностей данного типа треугольника.
- Первый метод основывается на построении перпендикуляра к основанию из вершины, которая расположена противоположно основанию. Этот перпендикуляр будет проходить через середину основания и служит для определения его положения.
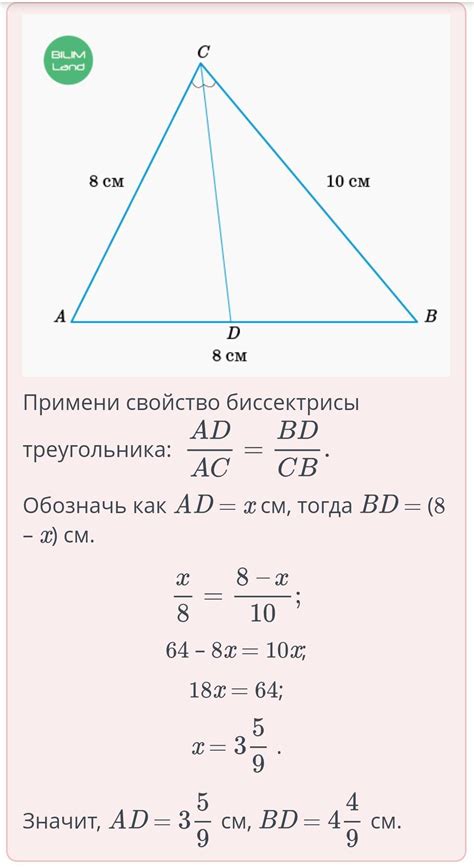
- Второй метод основан на использовании угла, напротив основания, который является биссектрисой прилежащего к нему угла. Путем построения этой биссектрисы и ее пересечения с противоположным ребром, можно определить положение основания.
- Третий метод связан с построением высоты, проведенной из вершины треугольника на основание. Высота будет проходить через середину основания, что позволяет определить его положение.
Каждый из этих геометрических методов обладает своими особенностями и применяется в зависимости от имеющихся данных и условий задачи. Знание этих методов позволяет точно определить положение основания в равнобедренном треугольнике и использовать эту информацию для решения геометрических задач и задач практического характера.
Использование особенностей внутренних и внешних касательных в равнобедренном треугольнике
В данном разделе рассмотрим интересный подход к определению местоположения основания в равнобедренном треугольнике, который основан на использовании особенностей внутренних и внешних касательных.
Основное свойство внутренней касательной в равнобедренном треугольнике заключается в том, что она делит основание на две равные части. Это позволяет нам легко определить положение основания при условии, что известна длина внутренней касательной и другие характеристики треугольника.
В то же время, внешняя касательная также имеет свои особенности. Она делит продолжение основания в отношении равном соотношению сторон равнобедренного треугольника. Это дает нам дополнительную информацию для определения местоположения основания и создает новые возможности для расчетов.
Используя сочетание информации о внутренней и внешней касательных, можно более точно определить местоположение основания в равнобедренном треугольнике. Это позволяет нам решать разнообразные задачи, связанные с этим классом треугольников, включая нахождение площади, высоты и других характеристик.
Метод оценки размещения основания в фигуре со сходными сторонами и углами
Этот метод основывается на наблюдении за фигурой и определении характеристик, которые отражают особенности размещения основания. Одним из ключевых факторов является симметричность треугольника относительно оси, проходящей через его вершину и центр основания. Визуально основание находится в осевом положении, когда его симметрично отражение в этой оси совпадает с исходным основанием. Однако, данная оценка является приблизительной и требует учета иных характеристик.
Кроме того, форма высоты треугольника также может быть использована для анализа размещения основания. В случае, когда высота проходит вблизи вершины треугольника и пересекает его основание близко к ее середине, можно предположить, что основание находится по центру фигуры и имеет равное расстояние до каждой из вершин. Это обусловлено свойством равномерного распределения площади фигуры.
Таким образом, метод визуальной оценки позволяет предварительно определить приближенное расположение основания в равнобедренном треугольнике, используя симметрию и форму фигуры. Однако, для получения точных результатов рекомендуется применять точные методы измерения и вычисления.
Ориентирование по длине и углам при наблюдении

В данном разделе рассматривается один из способов определения положения точки наблюдения в равнобедренном треугольнике. При использовании метода ориентирования по длине и углам, особое внимание уделяется измерению расстояний между точками и определению угловых отклонений. Этот метод позволяет определить точное местоположение точки наблюдения в треугольнике, основываясь на измерениях и ориентации по углам.
Интуитивное описание этого метода заключается в измерении длин отрезков и углов между ними при помощи инструментов и ориентации по ним. При наблюдении достаточно знать длину отрезка и угол, чтобы точно определить свое положение в равнобедренном треугольнике. При этом, углы могут быть измерены с использованием различных приборов или просто оценены глазом на основе ориентации по окружающим объектам.
Понимание принципов ориентирования по длине и углам позволяет более точно определить местоположение и движение внутри равнобедренного треугольника. Этот метод является важным инструментом для навигации и ориентации в различных ситуациях, таких как геодезия, картография, строительство и путешествия в незнакомых местах.
Аналитический подход к определению расположения базы в треугольнике с равными сторонами
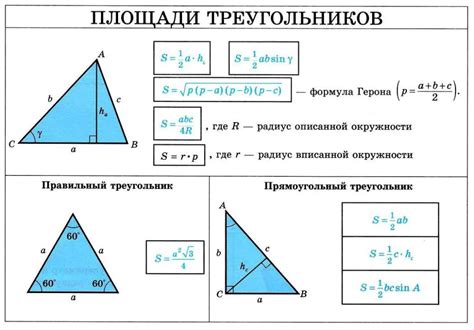
В данном разделе рассмотрим метод, основанный на аналитических подходах к определению расположения базы в треугольнике, где все стороны равны между собой.
Вместо использования терминов "местоположение" и "основание", мы будем исследовать "расположение" и "точку приложения", соответственно. Для избегания повторений, будем также использовать синонимы, чтобы представить общую идею данного раздела.
Аналитический метод основан на использовании геометрических формул и алгебраических выражений для определения координат точки приложения основания треугольника с равными сторонами. Основная идея заключается в применении известных свойств этого типа треугольников и преобразования геометрических данных в математические выражения.
Для начала, необходимо определить координаты вершин треугольника, используя известную информацию о его сторонах и углах. Затем мы можем применить специализированные формулы для вычисления координат точки приложения, например, координаты середины основания или координаты пятой вершины треугольника.
Аналитический подход позволяет более точно определить расположение базы в треугольнике с равными сторонами, поскольку он основан на математических моделях и точных вычислениях. Этот метод может быть полезен при решении различных задач, связанных с геометрией и треугольниками, таких как вычисление площади или длины сторон, определение координат других точек треугольника и многое другое.
В итоге, аналитический метод представляет собой мощный инструмент для определения точного расположения основания в равнобедренном треугольнике, что позволяет применять его в различных прикладных сферах, где требуется точность вычислений и анализа геометрических данных.
Вопрос-ответ

Какими методами можно определить местоположение основания в равнобедренном треугольнике?
В равнобедренном треугольнике можно определить местоположение основания с помощью различных методов. Некоторые из них включают использование высоты треугольника, биссектрисы угла при основании и медианы, проходящей через вершину основания.
Как работает метод определения местоположения основания с использованием высоты треугольника?
Для определения местоположения основания с использованием высоты треугольника нужно провести высоту из вершины этого треугольника. После этого основание будет находиться на пересечении высоты и основания треугольника. Для этого метода важно знать длину высоты и координаты вершины треугольника.
Что такое биссектриса угла при основании равнобедренного треугольника и как использовать ее для определения местоположения основания?
Биссектриса угла при основании равнобедренного треугольника - это отрезок, который делит данный угол пополам. Чтобы определить местоположение основания с помощью биссектрисы, нужно провести биссектрису угла при основании и найти точку пересечения с основанием треугольника. Зная координаты вершины треугольника и длины биссектрисы, можно рассчитать координаты основания.