Когда требуется определить, пересекаются ли два прямоугольника или нет, часто встает вопрос о выборе подхода и алгоритма для решения этой задачи. Независимо от того, целью является построение геометрического решения или выполнение вычислений на компьютере, понимание методов нахождения пересечения прямоугольников играет важную роль.
В данном разделе мы рассмотрим несколько подходов к определению пересечения прямоугольников, которые основываются на различных математических концепциях с целью предоставить полное представление о возможных методах. Каждый из этих методов обладает своими преимуществами и ограничениями, и их использование зависит от конкретной задачи, а также требований к производительности и точности решения.
Прежде всего, рассмотрим методы, основанные на вычислении координатной площади пересечения двух прямоугольников. Обычно это сводится к вычислению площади пересечения общей области двух фигур с известными координатами и размерами. Один из подходов заключается в использовании формулы площади прямоугольника и метода интервалов для определения координатного диапазона пересечения. Однако этот метод имеет свои недостатки, такие как не учет возможности смещения или поворота прямоугольников.
Другой подход основан на использовании векторных операций для определения пересекающихся сторон и углов прямоугольников. Суть этого подхода заключается в анализе векторов, соединяющих вершины прямоугольников, и проверке их взаимного положения с использованием скалярного произведения и других операций над векторами. Этот метод обычно требует более сложных вычислений, но позволяет более точно определить пересечение при различных взаимных расположениях прямоугольников.
Значение выявления пересечения прямоугольников по координатам
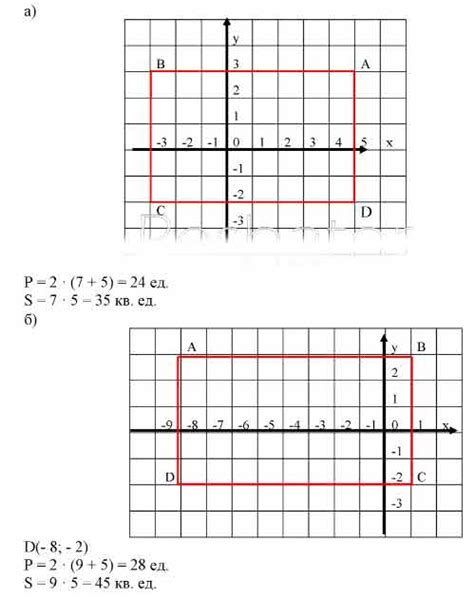
Путем анализа пересечения прямоугольников можно определить их взаимное положение относительно друг друга - пересекаются ли они вообще, перекрывают ли один другой или не имеют никакого контакта. Эта информация может быть полезна при создании программного обеспечения, которое работает с объектами, взаимодействующими на плоскости.
Одной из важных задач, связанных с выявлением пересечения прямоугольников, является определение области, где они пересекаются. Это позволяет рассчитать площадь пересечения, определить, сколько прямоугольников пересекается в конкретной точке и т.д. Эта информация может быть полезна при решении графических задач, таких как построение столкновений объектов в играх или построение трасс дорог в географических приложениях.
| Преимущества: |
|
Исследование способов обнаружения взаимного перекрытия прямоугольных областей
В данном разделе мы рассмотрим методы и подходы к определению наличия пересечения между прямоугольниками. Определение пересечения применяется во множестве задач и алгоритмов, где необходимо выявить и учесть ситуации, когда две области на плоскости перекрываются или нет. Мы рассмотрим различные подходы и алгоритмы, позволяющие эффективно определить, есть ли пересечение между заданными прямоугольниками.
Один из наиболее распространенных методов - это анализ координат вершин прямоугольников и их соотношение. Мы рассмотрим как геометрический подход, основанный на идее, что если один прямоугольник находится полностью внутри другого, то они пересекаются, так и алгоритмические методы, которые позволяют вычислить точные координаты пересечения.
Также мы рассмотрим альтернативные подходы к определению пересечения, основанные на использовании векторов, захватывающих общую площадь, а также на анализе длин и отношения сторон прямоугольников. Кроме того, будет представлен метод использования численных вычислений и аппроксимации для определения пересечения в случаях, когда прямоугольники имеют сложные формы или их вершины заданы вещественными координатами.
Метод разделения осей
Преимущество метода разделения осей заключается в его скорости работы и простоте реализации. Он может быть использован для определения пересечения не только прямоугольников, но и других геометрических фигур. Благодаря своей эффективности, метод разделения осей используется во множестве задач компьютерной графики, визуализации данных и коллизионного обнаружения.
Метод перебора точек

Рассмотрим один из возможных подходов к решению задачи определения пересечения прямоугольников. Этот метод основан на переборе всех возможных точек, которые могут принадлежать пересечению двух прямоугольников.
Во-первых, необходимо определить границы пространства, в котором могут находиться точки пересечения. В рамках данного метода можно ограничиться прямоугольником, охватывающим два исходных прямоугольника вместе с их возможным пересечением.
Далее следует перебрать все точки внутри этого прямоугольника с определенным шагом. Шаг может быть выбран достаточно маленьким, чтобы точность результата была приемлемой. Для каждой точки необходимо проверить, входит ли она внутрь обоих исходных прямоугольников. Если точка удовлетворяет этому условию, то она может быть точкой пересечения.
Важно отметить, что такой метод перебора точек может оказаться вычислительно затратным, особенно при больших размерах прямоугольников и малых значениях шага. Однако, он может быть полезен, если точность результата является первостепенной задачей, и время выполнения не является ограничивающим фактором.
Метод рекурсивного деления: эффективный подход к определению пересечения прямоугольников
Идея метода рекурсивного деления заключается в разбиении прямоугольников на более мелкие части, а затем определении пересечения для каждой из них отдельно. Это позволяет снизить вычислительную сложность задачи и улучшить производительность алгоритма.
Пересечение прямоугольников можно определить следующим образом с использованием метода рекурсивного деления:
- 1. Разделить каждый прямоугольник на четыре более мелких части;
- 2. Проверить пересечение каждой пары соответствующих частей прямоугольников;
- 3. Если у одной из пар частей прямоугольников есть пересечение, повторить шаги 1-2 для этих частей;
- 4. Если у всех пар частей прямоугольников есть пересечение, то исходные прямоугольники также пересекаются.
Метод рекурсивного деления позволяет эффективно определить пересечение прямоугольников, необходимые для дальнейшего анализа или решения задачи. За счет разбиения прямоугольников на меньшие части и проверки пересечения только этих частей, достигается снижение вычислительной сложности и экономия ресурсов системы.
Обнаружение перекрытия прямоугольников: алгоритм и принцип работы
Взаимное пересечение прямоугольников представляет собой важную задачу для определения, существует ли общая площадь между двумя прямоугольниками на плоскости. Умение эффективно проверять перекрытие прямоугольников необходимо во многих областях компьютерных наук и графики, таких как обработка изображений, компьютерное зрение, игровая разработка и многих других.
Алгоритм проверки пересечения прямоугольников - это математический алгоритм, который позволяет определить, имеют ли два прямоугольника общую часть. Идея алгоритма заключается в определении условий, при которых прямоугольники пересекаются и возвращает результат в виде булевого значения, показывающего, происходит ли пересечение или нет.
Один из простых методов для проверки пересечения прямоугольников - это сравнение их координатных значений. Если один из прямоугольников находится полностью слева от другого, то они не перекрываются. Аналогично, если один из прямоугольников находится полностью справа от другого, они также не пересекаются. Алгоритм также применяется для проверки вертикальных положений прямоугольников: если один прямоугольник находится полностью выше или ниже другого, они не перекрыты.
Более сложным алгоритмом проверки пересечения прямоугольников является алгоритм расчета пересекающихся границ. Он основан на проверке пересечения каждой границы одного прямоугольника с другим. Если хотя бы одна граница пересекает другую, то прямоугольники имеют общую площадь.
Алгоритмы проверки пересечения прямоугольников являются основной основой для сложных алгоритмов в компьютерной графике, таких как обнаружение столкновений в играх, выделение объектов на фотографиях, обработка изображений и многие другие. Изучение этих алгоритмов и методов обеспечивает понимание, как эффективно решать подобные задачи и создавать интуитивно понятные и мощные приложения.
Шаг 1: Определение координат четырех углов каждого прямоугольника
Для этого можно использовать различные методы и подходы в зависимости от предоставленных данных. Наиболее распространенный и простой способ - задать четыре угла прямоугольника с помощью точек, которые определяются их x и y координатами.
Таким образом, для каждого прямоугольника необходимо найти четыре точки: левый верхний угол, правый верхний угол, левый нижний угол и правый нижний угол. Эти точки будут иметь свои координаты и будут использоваться далее для определения пересечения прямоугольников.
Шаг 2: Анализ последовательности координат для определения взаимного положения прямоугольников
Для определения взаимного положения двух прямоугольников необходимо произвести сравнение и анализ координат их вершин. Этот шаг позволяет выявить пересечение или отсутствие пересечения между прямоугольниками в зависимости от расположения их вершин относительно друг друга.
Для начала нам потребуется анализировать, какие вершины прямоугольников лежат ближе друг к другу, а также определить, какие они принадлежат каждому из прямоугольников. Для этого можем использовать следующие сравнения и вычисления:
- Сравнение значения координаты x вершины каждого прямоугольника с соответствующими значениями координат x других вершин.
- Сравнение значения координаты y вершины каждого прямоугольника с соответствующими значениями координат y других вершин.
- Сравнение расстояний между вершинами каждого прямоугольника с суммой длин его сторон.
Вопрос-ответ

Как узнать, пересекаются ли два прямоугольника?
Для определения пересечения двух прямоугольников необходимо сравнить координаты их сторон. Если хотя бы одна из сторон одного прямоугольника пересекается с любой из сторон другого прямоугольника, то прямоугольники пересекаются.
Какие методы можно использовать для определения пересечения прямоугольников?
Для определения пересечения прямоугольников существует несколько методов. Один из них - метод сравнения координат, о котором уже упоминалось. Другой метод - использование геометрических формул векторного анализа, таких как проекция, скалярное произведение и евклидово расстояние. Эти методы позволяют точно определить, пересекаются ли прямоугольники и вычислить площадь их пересечения.
Можно ли определить точку пересечения двух прямоугольников?
Да, точку пересечения двух прямоугольников можно определить, если она существует. Для этого необходимо найти пересечение сторон каждого прямоугольника и вычислить координаты этой точки пересечения. Это можно сделать с использованием геометрических методов и алгоритмов.
Какой алгоритм наиболее эффективен для определения пересечения прямоугольников по координатам?
Наиболее эффективным алгоритмом для определения пересечения прямоугольников по координатам является алгоритм МТВ (Метод типичных координатных сечений). Он позволяет сократить количество сравнений координат сторон прямоугольников, основываясь на предварительно вычисленных данным алгоритмом типичных координатных сечениях.



