Взгляните на окружающий мир. Помните ли вы, как учились искать скрытое за поверхностью? Задачи геометрии как загадки, которые требуют разгадывания, дарят уникальную возможность нашему разуму испытать взлет и падение рационального мышления. Сегодня предлагаем вам одну из таких загадок, которая касается фигур в пространстве. Готовы провести наш виртуальный путь через точки и линии, вглядываясь в тайны геометрических конструкций? Тогда пристегните ремни, ведь мы отправляемся в шестое измерение – мир шестиугольников!
Знание геометрии дарит нам инструменты для изучения и анализа пространства, которое нас окружает. От того, как мы помним и применяем эти инструменты, зависит наше понимание мира. Основные понятия этой науки, такие как фигура, линия, угол и радиус, являются ключами к великой головоломке – загадке геометрии. Именно с помощью этих понятий мы сможем раскрыть тайну шестиугольника, понять его форму и размеры. Сегодня мы сконцентрируем внимание на радиусе вписанной окружности – загадочном показателе, который привязывает все стороны шестиугольника к его центру.
Для начала предлагаем представить фигуру, которую мы будем исследовать. Визуализируйте в уме шестиугольник – многогранный объект, который обладает шестью равными сторонами и шестью равными углами. Он имеет достаточно интересные свойства и может быть использован в самых разнообразных областях, от создания узоров до строительства больших сооружений. И вот пришло время потрогать грани этой формы, начертить линии поверхности и вместе разгадать загадку шестиугольника! Но прежде чем мы это сделаем, давайте уделем особое внимание окружности, которая вписана в нашу фигуру. Ведь именно она и ее радиус будут ключом к поиску стороны нашего геометрического пазла.
Определение геометрической фигуры, в которую может быть вписана окружность
В рамках данного раздела рассматривается одна из важных характеристик геометрической фигуры, а именно, возможность вписать окружность в данную фигуру. Вписанная окружность обладает особыми свойствами и может быть использована для решения различных задач и построений.
Говоря о вписанной окружности, имеется в виду окружность, которая полностью помещается внутри геометрической фигуры, касаясь всех ее сторон внутренним касанием. В отличие от описанной окружности, вписанная окружность лежит строго внутри фигуры и не выходит за ее границы.
Возможность вписать окружность в геометрическую фигуру является особой характеристикой этой фигуры. Некоторые фигуры, такие как круг, всегда могут содержать в себе вписанную окружность. Однако для других фигур, например треугольника или шестиугольника, возможность вписать окружность зависит от конкретных условий.
Вписанная окружность обладает рядом важных свойств и особенностей, которые делают ее полезным инструментом в геометрии. Знание о том, как определить геометрическую фигуру, в которую может быть вписана окружность, позволяет решать разнообразные задачи, связанные с этими фигурами, и использовать вписанную окружность в решении различных геометрических задач.
Связь между размером радиуса вписанной окружности и длиной стороны шестиугольника
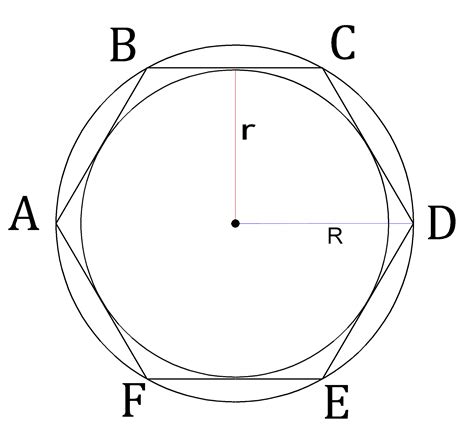
Этот раздел посвящен изучению прямой зависимости между значением радиуса вписанной окружности и длиной стороны шестиугольника. Мы рассмотрим, как изменения величины радиуса оказывают влияние на размер стороны шестиугольника, представим необходимые формулы и приведем примеры расчетов.
Этот аспект является важным при конструировании и изучении шестиугольников, так как позволяет определить сторону шестиугольника уже зная значение радиуса вписанной окружности и наоборот.
Для начала введем основные определения. Радиусом вписанной окружности называется расстояние от центра окружности до любой точки на ее границе. Стороны шестиугольника представляют собой отрезки, соединяющие соседние вершины шестиугольника.
При анализе связи между радиусом и стороной шестиугольника важно помнить, что эти величины тесно связаны друг с другом. При увеличении радиуса вписанной окружности, сторона шестиугольника также увеличивается, и наоборот, при уменьшении радиуса сторона шестиугольника уменьшается.
Для определения этой связи можно использовать различные математические формулы, позволяющие выразить сторону шестиугольника через радиус вписанной окружности и наоборот. Кроме того, можно провести соответствующие расчеты и воспользоваться значениями, полученными в различных исследованиях и опытах.
- Формула для вычисления длины стороны шестиугольника при известном радиусе вписанной окружности: S = 2 * R * sin(π/6).
- Обратная формула, позволяющая определить радиус вписанной окружности по известной длине стороны шестиугольника: R = s / (2 * sin(π/6)).
Приведенные формулы позволяют установить связь между радиусом вписанной окружности и длиной стороны шестиугольника, что является важным инструментом при решении геометрических задач и приложении этого знания в различных областях, таких как архитектура, инженерия и дизайн.
Конструкция для определения длины стороны шестиугольника
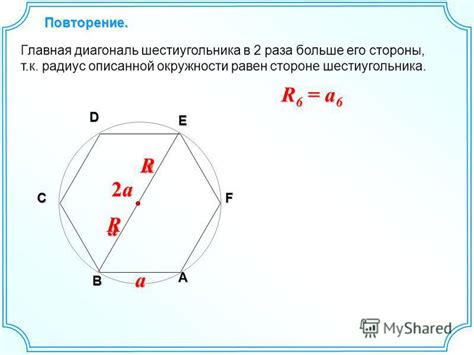
Этот раздел предоставит вам формулу, позволяющую рассчитать длину стороны шестиугольника. Узнав конкретные значения параметров и следуя данной инструкции, вы сможете получить точный результат, необходимый для вашего анализа или проектирования.
- Шаг 1: Подготовка исходных данных
- Шаг 2: Применение формулы
- Шаг 3: Проверка и адаптация результата
Прежде чем перейти непосредственно к расчетам, необходимо собрать все необходимые значения. Это включает в себя координаты центра вписанной окружности и радиус этой окружности. Запишите эти данные, чтобы в дальнейшем использовать их в формуле.
После сбора исходных данных вы можете приступить к вычислению длины стороны шестиугольника. Для этого применяется специальная формула, основанная на треугольниках.
Пройдите по каждому треугольнику, образованному при соединении центра вписанной окружности и точек пересечения линий с окружностью. Рассчитайте длину каждого из этих треугольников. Затем сложите полученные значения, чтобы получить общую длину стороны шестиугольника.
Полученный результат представляет собой длину стороны шестиугольника. Однако всегда целесообразно проверить и адаптировать его в соответствии с потребностями и целями вашего проекта. Обратите внимание на единицы измерения и произведите необходимые преобразования, чтобы получить итоговое значение, удовлетворяющее вашим требованиям.
Примеры вычислений стороны шестиугольника по радиусу вписанной окружности

В данном разделе мы рассмотрим несколько примеров, демонстрирующих способы вычисления стороны шестиугольника по известному радиусу вписанной окружности. Благодаря этим примерам вы сможете легко расчитать длину стороны шестиугольника, даже если у вас нет геометрических инструментов или доступа к специальному программному обеспечению.
Пример 1: Допустим, у нас имеется вписанная окружность радиусом R. Чтобы найти длину стороны шестиугольника, можно воспользоваться формулой L = 6R, где L - длина стороны шестиугольника. Таким образом, если радиус вписанной окружности равен 5 см, то длина стороны шестиугольника будет равна 30 см.
Пример 2: Предположим, что известна площадь шестиугольника, а также радиус вписанной окружности. Один из способов вычисления длины стороны шестиугольника в этом случае - использование формулы L = √(S/√3), где L - длина стороны шестиугольника, S - площадь шестиугольника. Например, если площадь шестиугольника составляет 100 см², а радиус вписанной окружности равен 4 см, то длина стороны шестиугольника будет примерно 10 см.
Пример 3: Еще одним методом определения длины стороны шестиугольника может быть использование формулы L = 2Rsin(π/6), где L - длина стороны шестиугольника, R - радиус вписанной окружности. Например, если радиус вписанной окружности равен 6 см, то длина стороны шестиугольника будет примерно 6 см.
Таким образом, по известному радиусу вписанной окружности можно легко вычислить сторону шестиугольника, используя соответствующие геометрические формулы. При этом следует учитывать различные особенности каждой формулы и подбирать наиболее подходящий метод для конкретной ситуации.
Вопрос-ответ

Чему равна сторона шестиугольника, если известен радиус вписанной окружности?
Для нахождения длины стороны шестиугольника, исходя из радиуса вписанной окружности, можно использовать следующую формулу: длина стороны равна двукратному значению радиуса, умноженного на тангенс 30 градусов.
Как узнать сторону шестиугольника, если известен радиус окружности, вписанной в него?
Для определения стороны шестиугольника по радиусу вписанной окружности нужно воспользоваться формулой: длина стороны равна удвоенному значению радиуса, умноженному на √3 (корень квадратный из 3).
Я знаю радиус вписанной окружности шестиугольника. Как мне найти длину его стороны?
Для определения длины стороны шестиугольника по радиусу вписанной окружности следует воспользоваться формулой: длина стороны равна двукратному значению радиуса, умноженному на tang 30° (тангенс 30 градусов).
Как определить сторону шестиугольника, если известен радиус окружности, которая вписана в него?
Длина стороны шестиугольника может быть найдена по формуле: длина стороны равна удвоенному значению радиуса, умноженному на корень квадратный из 3 (√3).
Можно ли определить сторону шестиугольника по радиусу вписанной окружности?
Да, можно определить длину стороны шестиугольника, зная радиус вписанной окружности. Для этого используется формула: длина стороны равна двукратному значению радиуса, умноженного на тангенс 30 градусов.



