Подробное понимание принципов определения объема пирамиды является неотъемлемой частью изучения трехмерной геометрии. Когда мы рассматриваем фигуры в трехмерном пространстве, важно иметь точное представление о их свойствах и характеристикам.
Одной из ключевых характеристик пирамиды является ее объем - это величина, отражающая количество трехмерного пространства, занимаемого данной фигурой. В данной статье мы рассмотрим подробное руководство по определению объема пирамиды по координатам ее вершин.
Вершины пирамиды являются основными элементами для расчета ее объема. Координаты этих вершин могут быть представлены в виде трехмерных точек в пространстве. Наша задача - восстановить геометрическую форму пирамиды и определить ее объем, используя эти координаты вершин.
Понятие пирамиды и ее особенности

Каждая пирамида имеет некоторые отличительные черты:
- Форма основания: основание пирамиды может быть в виде различных многоугольников, таких как треугольник, квадрат, пятиугольник и т.д.;
- Вершина: вершина пирамиды является точкой, которая соединяется с вершинами основания;
- Грани и ребра: у пирамиды есть грани, которые образуются путем соединения вершины с каждой вершиной основания, а также ребра, которые представляют собой линии, соединяющие вершину и вершины основания;
- Высота: высота пирамиды - это расстояние между ее вершиной и плоскостью основания.
Изучение особенностей пирамиды позволяет лучше понять ее форму, структуру и свойства, что в свою очередь способствует определению ее объема по заданным координатам вершин. Далее мы рассмотрим подробные методы для расчета объема пирамиды.
Определение пирамиды в геометрии

Понятие пирамиды играет важную роль в геометрии и может быть определено как вытянутая фигура, состоящая из вершины и плоской основы, которая соединяется с вершиной через триангуляцию.
В основе понимания пирамиды лежит представление её в виде основания и боковых граней, сходящихся в вершине. Определение пирамиды позволяет изучать и анализировать её геометрические свойства и отношения с другими фигурами.
Пирамида может иметь различную форму основания: треугольную, четырехугольную, пятиугольную и т.д. От выбранной формы основания зависит структура боковых граней пирамиды и её общий вид.
Боковые грани пирамиды являются треугольниками, а их количество определяется формой основания. Пересечение боковых граней друг с другом происходит в ребрах пирамиды.
Определение пирамиды в геометрии позволяет нам анализировать и вычислять различные характеристики этой фигуры, включая объем, площадь основания и боковых граней, а также длины ребер.
Шаг 1: Определение положения вершин пирамиды в пространстве

Каждая вершина пирамиды имеет свои координаты в пространстве. С помощью этих координат мы можем точно определить местонахождение каждой вершины относительно начала координатной системы.
Для этого нам понадобятся три числа, обозначающие координаты вершины по осям x, y и z. Ось x направлена горизонтально, ось y - вертикально вверх, а ось z - вертикально вглубь. Координаты могут быть выражены в любых единицах измерения, будь то метры, сантиметры или пиксели.
Определив координаты всех вершин пирамиды, мы сможем перейти к следующему шагу - вычислению объема пирамиды.
Определение координат вершин пирамиды в трехмерном пространстве
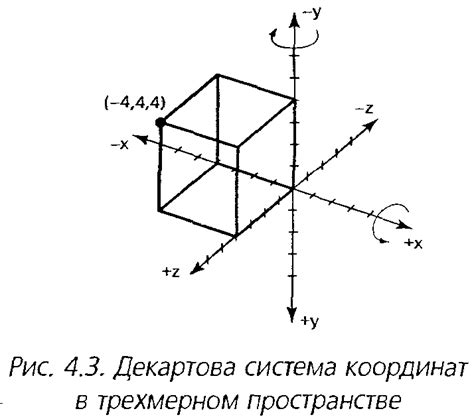
В этом разделе мы рассмотрим методы и подходы к определению координат вершин пирамиды в трехмерном пространстве. Мы изучим различные техники, которые позволят нам точно определить положение вершин пирамиды относительно координатной системы.
Определение координат вершин пирамиды в трехмерном пространстве
Для того чтобы определить координаты вершин пирамиды, мы должны учитывать положение и ориентацию самой пирамиды в трехмерном пространстве. Для начала, необходимо определить базовую точку пирамиды, которая может быть одной из вершин или центром основания пирамиды.
Затем, используя информацию о геометрических параметрах пирамиды, таких как высота и углы, мы можем определить координаты оставшихся вершин пирамиды. Это может быть достигнуто путем использования синусов и косинусов для нахождения координат вершин в трехмерном пространстве относительно базовой точки пирамиды.
Примечание: Важно помнить, что для определения координат вершин пирамиды, нам нужно иметь точные измерения и информацию о ее форме и размерах. Использование специализированного программного обеспечения или математических формул может значительно облегчить процесс определения координат вершин пирамиды в трехмерном пространстве.
Шаг 2: Определение длин сторон пирамиды
Для начала, необходимо вычислить расстояние между каждой парой вершин пирамиды. Это можно сделать с помощью формулы расстояния между двумя точками в трехмерном пространстве. Интуитивно, это расстояние представляет собой длину прямой линии, соединяющей две вершины пирамиды.
Чтобы определить длину ребра, следует найти максимальное расстояние между всеми возможными парами вершин. Таким образом, мы получим наибольшую сторону пирамиды, которая будет играть важную роль при вычислении ее объема.
Для более ясного представления результатов, рекомендуется использовать таблицу или список, в котором каждая строка будет соответствовать отдельному ребру пирамиды, а значения будут представлять длины соответствующих сторон.
Методы измерения длин ребер пирамиды и их значения
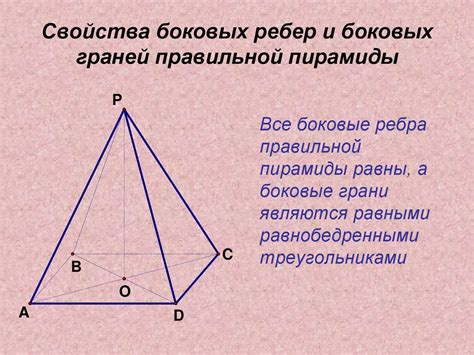
В данном разделе мы рассмотрим различные методы измерения длин ребер пирамиды и их важность при расчете объема данной геометрической фигуры. При измерении длин ребер пирамиды необходимо использовать определенные приемы и инструменты, чтобы получить точные значения и обеспечить верное определение объема пирамиды.
Измерение длины ребер пирамиды можно осуществлять с помощью геометрических инструментов, таких как линейка или метрологическая лента. Для этого необходимо определить начальную и конечную точки ребра и провести измерение между ними, учитывая все изгибы и повороты. Затем полученное значение должно быть записано для использования в дальнейших расчетах.
Важно учитывать, что длины ребер пирамиды могут иметь различные значения в зависимости от их положения и ориентации в пространстве. Некоторые ребра могут быть параллельными или совпадающими, что может влиять на общий объем пирамиды. Поэтому точное измерение каждого ребра является важным этапом при расчете объема пирамиды.
Кроме классических методов измерения ребер пирамиды, также существуют современные инструменты и техники, позволяющие получить более точные и надежные значения длин. Например, использование лазерного измерителя может значительно упростить процесс и повысить точность измерений. Также важно учитывать возможные погрешности и выбирать подходящий метод в зависимости от требуемой точности результата.
Шаг 3: Определение площадей граней пирамиды

Для начала мы рассмотрим метод, основанный на расчете площади треугольника с помощью его вершин. В таблице ниже представлены координаты вершин каждой грани пирамиды, а также вычисленные площади треугольников.
| Грань | Вершина A | Вершина B | Вершина C | Площадь |
|---|---|---|---|---|
| Грань 1 | (x1, y1, z1) | (x2, y2, z2) | (x3, y3, z3) | S1 |
| Грань 2 | (x4, y4, z4) | (x5, y5, z5) | (x6, y6, z6) | S2 |
| Грань 3 | (x7, y7, z7) | (x8, y8, z8) | (x9, y9, z9) | S3 |
После того, как мы вычислили площади каждой грани, мы можем использовать их значения для дальнейшего расчета объема пирамиды. Этот метод позволяет нам получить точные результаты в случае, если пирамида обладает правильной геометрией и вершины заданы верно.
Определение площадей граней пирамиды по координатам вершин
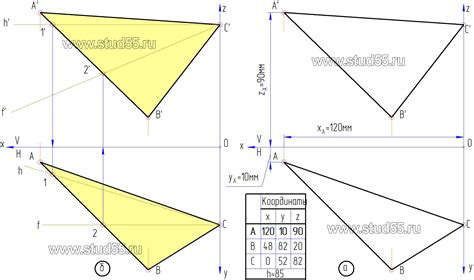
В этом разделе мы рассмотрим методы определения площадей граней пирамиды, основываясь на координатах ее вершин. Знание площадей граней позволяет лучше понять геометрическую структуру пирамиды и использовать это знание в решении различных задач.
Для определения площадей граней пирамиды по ее вершинам мы воспользуемся методом, основанным на использовании треугольников. Пирамида состоит из нескольких треугольных граней, и каждая из них имеет свою площадь. Для каждой грани пирамиды мы определим ее треугольную форму, используя координаты вершин, и затем применим соответствующую формулу для вычисления площади треугольника.
При определении площадей граней пирамиды по координатам ее вершин необходимо использовать формулу для площади треугольника, которая включает в себя длины его сторон и высоту. Для вычисления этих значений воспользуемся методами геометрии, такими как расстояние между двумя точками и длина вектора. После вычисления всех необходимых значений мы сможем определить площадь каждой грани пирамиды.
Определение площадей граней пирамиды по координатам вершин является важным шагом в анализе и изучении геометрии пирамиды. Знание площадей граней позволяет более глубоко понять ее форму и взаимное расположение граней, а также использовать это знание для решения различных задач и проблем, связанных с пирамидами.
| Грань | Площадь |
|---|---|
| Грань 1 | ... |
| Грань 2 | ... |
| Грань 3 | ... |
Вопрос-ответ

Как найти объем пирамиды по координатам вершин?
Чтобы найти объем пирамиды по координатам вершин, необходимо воспользоваться формулой Герона-Филона. Сначала вычисляется площадь основания, а затем высота пирамиды. После этого, используя найденные значения, производится расчет объема пирамиды. Подробное руководство с примерами и шагами расчета можно найти в статье.
Какие данные нужны для вычисления объема пирамиды с использованием координат вершин?
Для вычисления объема пирамиды по координатам вершин необходимы координаты всех вершин основания и координаты вершины пирамиды. Все эти данные позволят определить основание пирамиды, его площадь и высоту. Зная эти значения, можно применить формулу для расчета объема пирамиды.
Как применить формулу Герона-Филона для вычисления объема пирамиды?
Для применения формулы Герона-Филона необходимо сначала вычислить площадь основания пирамиды. Для этого используют формулу площади треугольника по его координатам. Затем, с помощью найденной площади и высоты, можно применить формулу для расчета объема пирамиды. Подробное руководство с пошаговыми инструкциями можно найти в статье.



