В мире математики существует огромное разнообразие функций, каждая из которых обладает своим уникальным графиком. График функции – это визуальное представление ее зависимости от переменных. Понять, как определить форму и характер графика, является одной из основных задач при изучении функций.
Определение графика функции – это процесс, требующий тщательного анализа и набора инструментов. Это похоже на раскрытие сложного головоломочного пазла, где каждый элемент отысканной картины раскрывает глубину и интенсивность взаимосвязей переменных. График функции – это графическое отображение значений функции, где она исследуется на своем природном поле, расположенном на пересечении осей координат.
Язык математики наполнен множеством терминов и обозначений, без которых невозможно осмыслить этот магический мир функций. Определить график функции – значит понять все его особенности: точки перегиба, максимумы и минимумы, асимптоты и многое другое. Осознавая все признаки, благодаря которым определить форму графика становится возможным, мы получаем возможность насладиться красотой математики и раскрыть потенциал лежащих в основе неделимых составляющих объективной реальности.
Роль функций в математике и её основные понятия

Понятие функции в математике основывается на идеи отображения, где каждому элементу из некоторого множества (называемого областью определения) сопоставляется ровно один элемент другого множества (называемого множеством значений). Функции могут быть представлены аналитически, с помощью формул и уравнений, или графически, через построение графиков, и обладают различными свойствами, такими как непрерывность, дифференцируемость или монотонность.
Основные понятия, связанные с функциями, включают понятия аргумента и значения, области определения и значений, соответственно. Аргумент представляет собой входное значение функции, в то время как значение - выходное значение, получаемое в результате применения функции к аргументу. Область определения определяет, какие значения может принимать аргумент, а область значений - какие значения могут быть получены в результате выполнения функции.
Изучение функций и их графиков позволяет анализировать их свойства и поведение, такие как экстремумы, асимптоты, пересечения с осями координат и т. д. Графики функций можно использовать для визуализации математических моделей, изучения изменений значений в зависимости от аргумента и построения прогнозов в различных областях науки и инженерии.
Значение графика функции для анализа её поведения

График функции позволяет нам визуализировать, как значения функции варьируются при различных входных значениях. Анализируя график, мы можем определить основные характеристики функции, такие как экстремумы, интервалы возрастания и убывания, асимптоты, точки разрыва и особые точки.
Понимание поведения функции в различных областях определения может помочь нам решать уравнения и неравенства, находить максимальные и минимальные значения функции, определять её симметричность или несимметричность относительно осей координат, а также предсказывать её поведение при изменении входных параметров.
Использование графика функции как инструмента для понимания её поведения является важным аспектом математического анализа и помогает нам проникнуть в суть функций, их свойств и особенностей. Отличное понимание графика функции помогает нам решать задачи из различных областей, включая физику, экономику и инженерию.
График линейной функции: основные свойства и форма
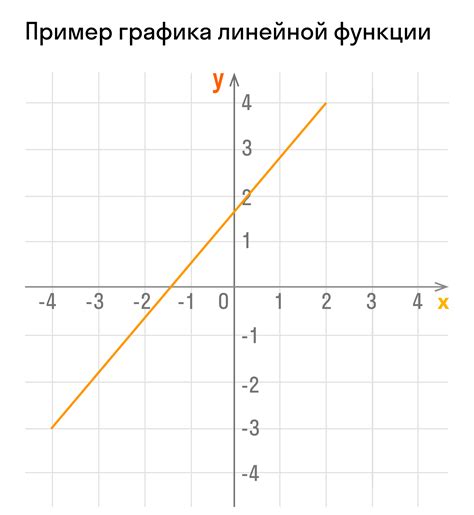
В данном разделе мы рассмотрим основные характеристики и форму графика линейной функции, обозначим их особенности и способы анализа.
| Свойство | Описание |
|---|---|
| Наклон прямой | Линейная функция характеризуется постоянным наклоном, который определяет ее поведение на графике. |
| Точка пересечения с осью ординат | График линейной функции всегда пересекает ось ординат в некоторой точке, которая определяет значение свободного коэффициента. |
| Уровнение прямой | Линейную функцию можно описать уравнением Ax + By = C, где A, B и C - это коэффициенты, определяемые свойствами функции. |
| Изменение значений | График линейной функции является прямой линией на плоскости, характеризующейся постоянным изменением значений при изменении аргумента. |
Анализ формы графика линейной функции позволяет нам определить ее характер и взаимосвязь между аргументом и значением функции. Улучшение навыков в определении и анализе графиков функций позволяет лучше понять и применять их в решении разнообразных математических задач.
Определение вида графика параболической функции: ключевые особенности

Для успешного анализа и понимания графика параболической функции необходимо уметь определить ее визуальные признаки. Однако, когда речь идет об определении типовых характеристик, важно избегать шаблонного использования понятий "Как", "определить", "график", "функции:", "советы" и "признаки". В данном разделе мы рассмотрим ключевые особенности, которые помогут вам точнее идентифицировать вид параболического графика, ориентируясь на его форму и расположение относительно осей координат.
1. Симметрия: В основе параболического графика лежит симметричность, и это является одним из главных признаков. Исследуйте, имеет ли график параболы ось симметрии, где симметричные точки находятся на одинаковом расстоянии от данной оси.
2. Вершина параболы: Важным элементом понимания параболической функции является ее вершина. Она представляет точку, где график достигает наивысшей или наименьшей точки, в зависимости от направления открытости параболы. При анализе параболы обратите внимание на ее вершину и особенности ее расположения.
3. Направление открытости: Различные параболические функции могут быть направлены вверх или вниз в зависимости от знака коэффициента при старшем члене параболы. Изучите направление открытости параболы, чтобы обнаружить особенности ее вида и тренда.
4. Расстояние до оси OX: Относительное положение графика относительно оси OX также является важным признаком определения параболической функции. Исследуйте, насколько график поднимается над осью OX или опускается под нее.
Запомните, что определение вида параболического графика основывается на анализе его визуальных характеристик. Наличие симметрии, вершины, направления открытости и относительного положения относительно оси OX являются ключевыми признаками, помогающими вам более точно определить информацию, закодированную на графике.
Особенности симметрии графиков функций: как ее распознать
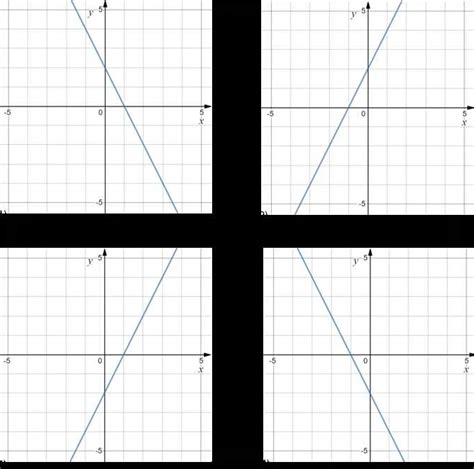
- Симметрия относительно оси абсцисс. Если график функции симметричен относительно оси абсцисс, то это означает, что при изменении знака аргумента функции ее значения остаются неизменными. Мы рассмотрим, как различить данную симметрию и как она влияет на характеристики функции.
- Симметрия по центру. Симметрия графика функции относительно некоторой точки называется симметрией по центру. Мы рассмотрим, как определить центр симметрии и какие характеристики графика функции можно извлечь из этого свойства.
- Комбинированная симметрия. Некоторые графики функций обладают комбинированной симметрией, то есть сочетанием нескольких видов симметрии. Мы изучим различные комбинации симметрии и узнаем, какая информация о функции может быть получена из каждой симметричной особенности.
Характеристики и форма графика экспоненциальной функции
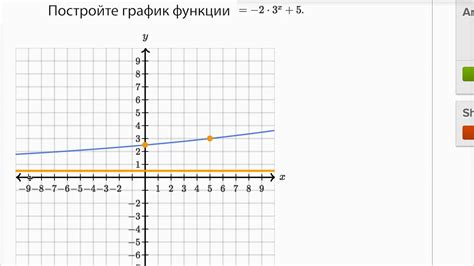
Раздел посвящен изучению особенностей и внешнего вида графиков экспоненциальных функций. Здесь мы рассмотрим характеристики, которые помогут понять и описать форму графика данного типа функции.
Как распознать периодическую формулу графика

Некоторые функции обладают особенностью, которая позволяет заметить закономерности в их графиках. Эти функции имеют периодический характер, т.е. их графики повторяются через определенные интервалы. Умение распознать периодическую формулу графика может быть полезным при анализе и описании различных процессов и явлений.
Если вы хотите определить, является ли график функции периодическим, обратите внимание на несколько ключевых признаков. Во-первых, периодическая функция будет иметь повторяющийся узор или форму, который можно выделить на графике. В этом случае можно говорить о графическом равенстве функции на разных интервалах, что указывает на наличие периода.
Во-вторых, у периодической функции будет существовать период, т.е. конкретное значение аргумента, при котором график функции повторяется снова. Это значит, что при изменении аргумента на значение периода функция принимает такое же значение, как и на предыдущем периоде.
Кроме того, периодическая формула графика может иметь специфические свойства, такие как симметрия, периодичность по обоим осям, особые точки и интервалы. Важно уметь улавливать эти особенности и использовать их для определения периодичности графика функции.
Выделение периодической формулы графика функции играет важную роль в анализе и исследовании процессов и явлений, где она может быть полезна в построении моделей, предсказании будущих значений и общем понимании закономерностей. Теперь, когда вы знаете несколько признаков и подходов для определения периодического графика функции, вы можете использовать этот инструмент для своих задач и поиска новых интересных закономерностей в мире математики и науки в целом.
Особенности графиков тригонометрических функций
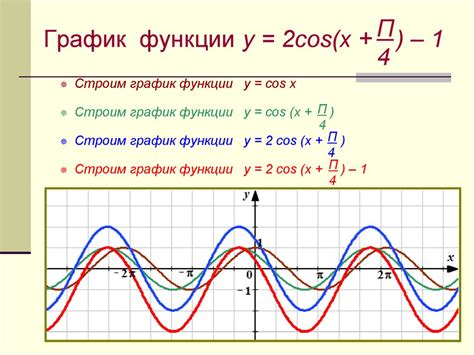
Графики тригонометрических функций отличаются от графиков обычных функций и имеют свои уникальные особенности. Они обладают периодичностью и симметрией, что позволяет увидеть определенные закономерности и поведение функций на протяжении определенного интервала.
Одним из важных понятий в графиках тригонометрических функций является период функции. Период определяет минимальное положительное значение x, на котором функция повторяется. Знание периода позволяет определить интервал, на котором требуется строить график.
Также нужно обратить внимание на значение амплитуды – наибольшего расстояния между графиком функции и осью OX. Амплитуда определяет вертикальное изменение функции и влияет на высоту графика.
Графики тригонометрических функций также можно классифицировать по их ограниченности и монотонности. Некоторые функции имеют ограниченный диапазон значений, в то время как другие – нет. Некоторые функции могут быть монотонными, т.е. строго возрастающими или убывающими в определенном интервале, тогда как другие могут иметь точки экстремума или периодически изменять свое поведение.
Понимание основных особенностей графиков тригонометрических функций является ключевым для успешного решения задач и анализа явлений в различных областях науки и техники.
Асимптоты графика функции: основные концепции и способы определения
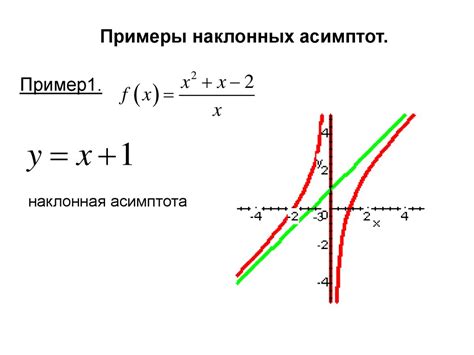
Определение асимптоты графика функции должно учитывать ее взаимосвязь с функцией, предельное значение функции при стремлении аргумента к бесконечности, а также характер поведения графика на бесконечно удаленных значениях аргумента.
Для определения вертикальной асимптоты графика функции необходимо найти значения, при которых функция не определена. Эти значения могут быть пределами на бесконечности, делением на ноль или возведением в отрицательную степень.
Горизонтальная асимптота графика функции определяется при стремлении аргумента к бесконечности. Если функция имеет предел в бесконечности, то график функции будет приближаться к горизонтальной прямой, которую мы и называем асимптотой.
Наклонная асимптота графика функции может существовать только при наличии горизонтальной асимптоты. Она определяется тем, как функция ведет себя на бесконечности и как она приближается к горизонтальной асимптоте.
- Для определения наклонной асимптоты можно использовать деление многочленов.
- Также можно использовать производные функции для определения наклонной асимптоты.
- Уточнение графика функции и определение асимптот происходит с помощью анализа поведения функции на участке около асимптоты.
Понимание основных концепций и способов определения асимптот графика функции поможет нам более точно представить поведение функции на бесконечно удаленных значениях аргумента и строить график функции с большей грамотностью.
Вопрос-ответ

Можно ли определить график функции только по ее аналитическому выражению?
Да, определить график функции можно по ее аналитическому выражению, если известны основные признаки функции, такие как точки пересечения осей, экстремумы, интервалы возрастания и убывания, асимптоты и другие.
Какие признаки функции помогают определить ее график?
Для определения графика функции необходимо узнать ее основные признаки, такие как точки пересечения осей, экстремумы, интервалы возрастания и убывания, асимптоты и другие. Эти признаки позволяют более точно представить и нарисовать график функции.
Какие инструменты можно использовать для построения графика функции?
Для построения графика функции можно использовать различные инструменты, такие как математические программы, графические калькуляторы, онлайн-сервисы для построения графиков. Возможности этих инструментов позволяют строить графики функций с высокой точностью и гибкостью.
Какие основные ошибки допускают при определении графика функции?
При определении графика функции можно допустить ошибки, такие как неправильная интерпретация аналитической записи функции, неправильное определение основных признаков функции, недостаточное количество точек для построения графика, неправильные масштабы на осях координат. Все эти ошибки могут привести к неверному представлению графика функции.
Какую информацию о функции можно получить по ее графику?
По графику функции можно получить различную информацию, такую как точки пересечения осей, наличие и тип экстремумов, интервалы возрастания и убывания, наличие асимптот и другие признаки функции. Также по графику можно примерно оценить поведение функции в различных областях и решать задачи, связанные с функциональной зависимостью.
Как определить график функции?
Для определения графика функции необходимо анализировать ее уравнение и определять основные характеристики: точки пересечения осей, экстремумы, интервалы монотонности и выпуклости, асимптоты и другие особенности.