В мире математики существует множество красивых и глубоких концепций, которые зачастую кажутся нам абсолютно непонятными. Одной из таких концепций является хорда, которая стягивает дугу. Но что означает это загадочное определение? Как можно найти такую хорду и как она связана с измерением углов?
Для начинающих математиков или любознательных умов представляется огромной задачей войти в мир этой темы, но несмотря на это, разобраться в основах и найти хорду, сжимающую дугу в 60 градусов, можно с некоторыми усилиями и пониманием.
В данном руководстве мы рассмотрим ключевые понятия, которые помогут нам разобраться в структуре хорды и ее связи с дугой. Мы научимся анализировать углы и применять геометрические законы, чтобы точно определить, какая именно хорда сжимает дугу на 60 градусов.
Основы геометрии для новичков

В данном разделе мы познакомимся с основами геометрии, которые помогут вам лучше понять и применять геометрические концепции. Здесь вы найдете некоторые ключевые понятия и свойства, которые описывают отношения и формы в пространстве.
| Термин | Описание |
|---|---|
| Прямая | Это одномерный объект, состоящий из бесконечного числа точек, расположенных на одной линии. |
| Угол | Это область в пространстве между двумя лучами, которые имеют общее начало и называются стартовым и конечным лучами. |
| Треугольник | Это фигура, состоящая из трех отрезков, соединяющих три точки. |
| Параллельные прямые | Это две прямые, которые никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга. |
| Перпендикулярные прямые | Это две прямые, которые пересекаются друг с другом и образуют прямой угол. |
Это лишь небольшая часть основ геометрии, которые пригодятся вам при изучении и применении геометрических концепций. Знание этих концепций позволит вам с легкостью оперировать фигурами и отношениями между ними, что сделает вашу работу с геометрией более эффективной и удобной.
Значение хорды, конгруэнтной данной дуге
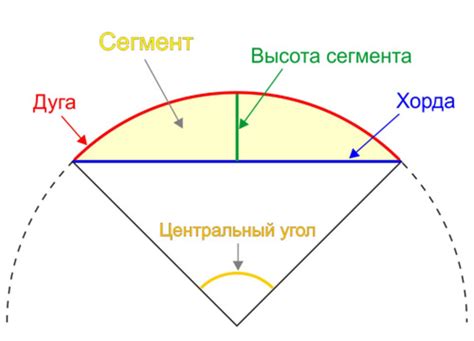
Длина хорды стягивающей дугу может быть определена с использованием геометрических методов, основанных на знании углов и длин других известных отрезков. Найдя значение хорды, мы можем рассчитать различные аспекты, такие как расстояние между точками дуги или площадь сектора, ограниченного этой дугой и хордой.
Существует несколько методов для нахождения длины хорды стягивающей дугу. Один из них, основанный на теореме синусов, позволяет вычислить длину хорды с использованием знания радиуса окружности, на которой находится дуга, и известного угла, охватываемого дугой. Другой метод основан на использовании формулы для нахождения длины хорды с помощью расстояния до центра окружности и длины хорды перпендикулярной к искомой хорде.
- Метод 1: использование теоремы синусов
- Метод 2: использование формулы для длины хорды
Оба метода имеют свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и имеющейся информации. На практике, для нахождения длины хорды, рекомендуется использовать компьютерные программы или онлайн-ресурсы, которые могут автоматически выполнить соответствующие вычисления.
Путь к решению: основные этапы
В данном разделе мы рассмотрим основные шаги, которые помогут вам найти необходимую хорду, стягивающую дугу под углом в 60 градусов. Будут представлены простые и понятные инструкции, которые помогут вам успешно выполнить поставленную задачу.
- Определение центра дуги: первый шаг в решении задачи - определить центр дуги. Для этого вам понадобится следующие инструменты: ... Методика... После определения центра дуги, вы сможете перейти к следующему шагу.
- Измерение радиуса: после определения центра, необходимо измерить радиус дуги. Радиус – это расстояние от центра дуги до ее края. Высчитав точное значение радиуса, вы сможете перейти к следующему этапу.
- Расчёт по формуле: на данном этапе вам понадобится математическая формула.... Необходимо использовать данную формулу, подставив вместо переменных известные значения, чтобы найти искомую хорду.
- Проверка результата: после проведения расчетов, важно проверить полученный результат. Не забывайте учитывать погрешности измерений и возможные ошибки при расчетах.
- Итоговые действия: в данном шаге необходимо привести итоговый результат и описать дальнейшие действия, которые могут потребоваться в зависимости от задачи.
Процесс измерения угла в 60 градусов
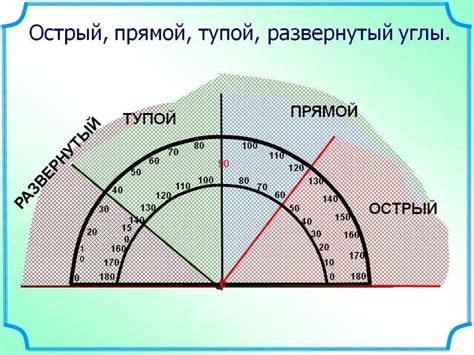
В этом разделе мы рассмотрим процесс определения угла величиной 60 градусов, без описания поиска стягивающей дуги или использования хорд.
Когда нам необходимо измерить угол, мы должны использовать определенные инструменты и методы. Для измерения угла в 60 градусов мы можем воспользоваться специальной измерительной инструментацией, такой как гониометр или профессиональный угломер. Эти инструменты позволяют нам точно определить угол и его величину, основываясь на принципах математики и геометрии.
Прежде чем измерять угол, необходимо установить точку начала и точку конца отсчета. Это может быть ориентир на плоскости или определенная геометрическая фигура, например, угол. Затем, используя инструмент для измерения углов, мы сможем определить расстояние между этими точками и получить числовое значение угла в градусах.
Измерение угла в 60 градусов важно в различных областях, таких как строительство, дизайн, геодезия и многое другое. Точность и надежность измерения угла играют значимую роль в проектах и работах, где требуется точное позиционирование и геометрическая согласованность.
Использование транспортира для определения угла
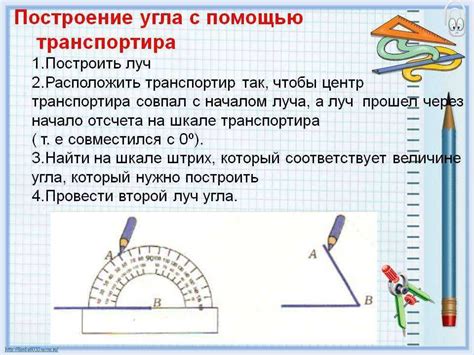
В данном разделе мы рассмотрим методику использования транспортира в измерении угла. Транспортир представляет собой инструмент, способный помочь вам определить точный угол между двумя отрезками в плоскости. Это особенно полезно при поиске хорды, стягивающей заданную дугу.
Угол – это мера поворота между двумя линиями вокруг общей точки. В нашем случае, хорда, стягивающая дугу, образует угол 60 градусов. Транспортир позволит нам убедиться, что выбранная нами хорда соответствует заданному углу.
Шаг 1: Расположите транспортир на плоскости и поверните его так, чтобы одна из его сторон совпадала с одним из отрезков, образующих хорду. Транспортир должен прилегать к обоим отрезкам в точке, где они пересекаются.
Шаг 2: Обратите внимание на шкалу транспортира и найдите отметку, соответствующую заданному углу в 60 градусов. Обычно она обозначена точкой или стрелкой.
Шаг 3: Поверните транспортир вокруг точки пересечения отрезков так, чтобы заданная отметка совпала с вторым отрезком. Убедитесь, что транспортир все еще примыкает к обоим отрезкам.
Шаг 4: Проверьте, что рассматриваемая хорда проходит через точку пересечения отрезков. Если это так, то эта хорда стягивает дугу под заданным углом 60 градусов.
Важно помнить, что использование транспортира является лишь одним из методов определения хорды стягивающей дугу в 60 градусов. В зависимости от ситуации и доступности инструментов, вы можете использовать и другие подходы для выполнения этой задачи.
Равносторонний треугольник: простое руководство для воспроизведения

В этом разделе мы изучим, как нарисовать равносторонний треугольник, который имеет все три стороны одинаковой длины и все три угла равны. Равносторонний треугольник может быть создан с помощью нескольких простых шагов, и наша инструкция поможет вам освоить это с легкостью.
Шаг 1: Подготовьте рабочую поверхность Перед тем, как начать рисовать равносторонний треугольник, выберите рабочую поверхность, на которой будете работать. Это может быть лист бумаги или холст. Убедитесь, что ваша рабочая поверхность пуста и чиста, чтобы избежать помех и отвлечений во время рисования. |
Шаг 2: Рисуйте основу треугольника Начните с рисования вертикальной линии на вашей рабочей поверхности. Это будет основа равностороннего треугольника. Обозначьте середину этой линии, так как она будет являться точкой встречи всех трех сторон треугольника. |
Шаг 3: Рисуйте боковые стороны Из точки встречи основы треугольника проведите две линии, исходящие вверх в виде угла под углом в 60 градусов. Эти линии будут боковыми сторонами равностороннего треугольника. Убедитесь, что обе линии имеют одинаковую длину, чтобы гарантировать равные стороны треугольника. |
Шаг 4: Замыкайте треугольник Соедините концы боковых сторон равностороннего треугольника, чтобы получить закрытый контур. Убедитесь, что углы между боковыми сторонами и основой равны 60 градусам каждый. Ваш равносторонний треугольник готов! |
Теперь вы знаете, как нарисовать равносторонний треугольник безо всяких сложностей. Практикуйтесь в рисовании и исследуйте возможности этой удивительной геометрической формы. Равносторонние треугольники часто встречаются в различных областях, таких как строительство и дизайн, поэтому это полезное умение для начинающих в любой сфере.
Расчет длины хорды при заданном угле

Этот раздел посвящен методике определения длины хорды, которая стягивает дугу под определенным углом. Вместо прямого указания, как найти хорду, мы рассмотрим алгоритм расчета длины хорды на основе заданного угла.
Для начала, необходимо понять, что хорда - это отрезок, соединяющий две точки на окружности. Угол же, образуемый этой хордой и радиусом, позволяет определить длину хорды. Путем применения тригонометрических пропорций и формулы угловой меры, мы можем получить точное значение искомой длины.
Давайте представим себе задачу: у нас есть окружность с известным радиусом и нам нужно найти длину хорды, образующей угол в 60 градусов с радиусом. Для такого расчета нам понадобятся формулы синуса и косинуса, которые позволяют определить отношение сторон треугольника с углом 60 градусов.
Применяя формулу, мы сможем точно рассчитать длину хорды, исходя из заданного угла, радиуса окружности и использования тригонометрических функций. Такой подход обеспечит нам точность и результативность в вычислениях, позволяя находить длину хорды для различных углов, не только для 60 градусов.
Особенности определения хорды в различных геометрических фигурах
В случае квадрата, каждая сторона может быть рассмотрена как хорда, соединяющая две вершины. Для прямоугольника, у которого все углы прямые, существует две горизонтальные и две вертикальные хорды, соединяющие противоположные вершины. В треугольнике переменные стороны могут служить хордами, соединяющими соответствующие вершины.
- В круге хорда является отрезком, соединяющим две точки на окружности. Хорда, проходящая через центр окружности, называется диаметром. Диаметр является самой длинной хордой и делит окружность на две равные дуги.
- В эллипсе хорда является линией, соединяющей две точки, лежащие на границе эллипса. Эллипс имеет два фокуса, и сумма расстояний от эллипса до каждого фокуса одинакова для всех точек на эллипсе. Хорды в эллипсе обладают разными свойствами, связанными с его формой и размерами.
- В острых треугольниках хорды, соединяющие вершины, могут быть использованы для решения разнообразных задач, например, для определения высоты или медианы треугольника. В тупоугольном треугольнике хорды, соединяющие вершины, не могут быть использованы в качестве высоты или медианы, но они все равно являются важными элементами для изучения особенностей фигуры.
Важно помнить, что нахождение хорды зависит от конкретной геометрической фигуры, ее особенностей и задачи, которую необходимо решить. Понимание этих особенностей поможет вам более точно и эффективно работать с хордами в разных фигурах и использовать их для решения задач.
Нахождение хорды в круге

В данном разделе мы рассмотрим методы и принципы определения хорды внутри круга. Хорда представляет собой отрезок, соединяющий две точки на окружности. Определение хорды составляет важную часть геометрии и находит применение в различных областях, таких как архитектура, строительство и дизайн. Мы рассмотрим основные концепции и шаги, позволяющие точно определить хорду внутри круга.
Определение геометрической характеристики: Для начала необходимо определить центр круга - точку, равноудаленную от всех точек на окружности. Затем можно приступить к поиску хорды, которая будет стягивать заданную дугу в определенном угле, например, в 60 градусов. Хорда должна проходить через точку, находящуюся на окружности и лежащую на прямой, образованной центром круга и концами дуги.
Различные способы определения: Существует несколько способов нахождения хорды в круге. Один из них - использование теоремы о перпендикулярности касательной и радиуса, которая позволяет найти точки пересечения хорды с окружностью. Другим способом является использование формул и вычислений на основе углов и радиусов круга. Подходящий метод выбирается в зависимости от известных данных и образуемых условий.
Использование графических и вычислительных инструментов: Современные технологии и программы позволяют упростить процесс нахождения хорды в круге. Графические инструменты, такие как компьютерные программы для построения и редактирования фигур, позволяют наглядно визуализировать геометрические объекты и получить точные результаты. Кроме того, вычислительные инструменты, такие как электронные таблицы или специализированные программы, могут быть использованы для выполнения сложных математических расчетов и получения точных значений параметров хорды.
В заключении, нахождение хорды в круге требует понимания основных геометрических принципов и использования соответствующих методов. Независимо от способа нахождения, необходимо быть внимательным и точным в работе с геометрическими объектами, чтобы получить достоверные результаты.
Поиск линейного сегмента в эллипсе и параболе
Этот раздел посвящен методам нахождения хорды в кривых типа эллипса и параболы. Мы рассмотрим основные принципы и подходы, которые помогут вам найти и определить линейный сегмент в данных математических объектах, также известных как конические сечения.
Перед тем как мы приступим к деталям, важно понять, что эллипс и парабола представляют собой две различные геометрические фигуры с уникальными характеристиками. Наш раздел охватит оба варианта и объяснит особенности каждого из них.
Мы рассмотрим различные подходы, которые можно использовать для поиска хорды в эллипсе и параболе. Одним из них является использование математических формул и уравнений, связанных с этими кривыми. Вторым подходом будет графическое представление с использованием геометрических конструкций и инструментов.
Для эллипса будут рассмотрены методы, основанные на определении фокусных точек и применении соответствующих свойств и уравнений для нахождения хорды. Затем мы изучим параболу и рассмотрим способы использования ее фокуса и осей симметрии для определения хорды.
Важно отметить, что представленные методы подходят как для начинающих, так и для более продвинутых математиков. Они помогут вам лучше понять и развить свои навыки в области геометрии и анализа кривых. Готовы начать поиск хорды в эллипсе и параболе? Тогда давайте приступим!
Сложности при определении поперечных линий в разносторонних фигурах
При изучении фигур с конечным числом сторон и углов возникает необходимость определить поперечные линии, такие как хорды, которые пересекают дуги или стороны фигур. Однако процесс нахождения этих линий может быть сложным из-за ряда проблем, с которыми сталкиваются исследователи.
Несовершенная информация: Во многих случаях, чтобы определить хорду, нам требуется знать точные значения углов и длин сторон фигуры. Однако в реальных условиях информация может быть приблизительной или недостаточной, что затрудняет процесс определения искомых поперечных линий.
Геометрическая сложность: Изучение поперечных линий требует применения различных геометрических методов и инструментов. Это может включать использование теорем, формул и построение соответствующих фигур. Отсутствие достаточной геометрической подготовки может затруднить понимание процесса нахождения хорды.
Множество вариантов: В зависимости от формы и размеров фигуры, возможно существование нескольких вариантов поперечных линий, способных стягивать дугу под определенным углом. Это требует от исследователя принятия решения о выборе наиболее подходящей хорды в конкретной ситуации.
Выбор избыточности: В некоторых случаях может возникнуть проблема определения наиболее подходящей поперечной линии из множества возможных вариантов. Интуитивный выбор может привести к неточным результатам или неправильному пониманию исследуемой фигуры.
В результате, при поиске поперечных линий, таких как хорда стягивающая дугу под определенным углом, необходимо учитывать сложности, связанные с получением достоверной информации, использованием геометрических методов, выбором подходящей линии и представлением точных результатов. Только учитывая эти сложности и преодолевая их, мы сможем успешно находить хорды в разносторонних фигурах.
Вопрос-ответ

Как найти хорду стягивающую дугу в 60 градусов?
Для того, чтобы найти хорду, стягивающую дугу в 60 градусов, нужно выполнить несколько шагов. Во-первых, определите радиус окружности, на которой находится дуга. Затем умножьте радиус на удвоенное значение синуса половины угла дуги. Таким образом, вы получите длину хорды, которую ищете. Отметьте начало и конец хорды на окружности, и проведите прямую через эти точки - это и будет хорда, стягивающая дугу в 60 градусов.
Как найти значение угла для стягивания хорды дуги в 60 градусов?
Чтобы найти значение угла для стягивания хорды дуги в 60 градусов, нужно воспользоваться формулой синуса. Сначала найдите длину хорды и радиус окружности, на которой находится дуга. Затем поделите длину хорды на удвоенное значение радиуса. Извлеките арксинус этого отношения и умножьте полученное значение на 2. Таким образом, вы получите угол, который нужно стянуть этой хордой для создания дуги в 60 градусов.
Существуют ли какие-то дополнительные формулы или методы для нахождения хорды стягивающей дугу в 60 градусов?
Да, помимо основной формулы, существуют и другие методы для нахождения хорды, стягивающей дугу в 60 градусов. Например, воспользовавшись геометрической конструкцией, вы можете провести радиус, перпендикулярный хорде и проходящий через ее середину. Затем, используя некоторые свойства треугольника, можно найти длину хорды. Важно отметить, что каждый способ имеет свои особенности и может быть более или менее удобным в различных ситуациях.
Что нужно знать о радиусе и дуге, чтобы успешно найти хорду стягивающую дугу в 60 градусов?
Для успешного нахождения хорды, стягивающей дугу в 60 градусов, необходимо знать значения радиуса окружности и угла дуги. Радиус позволяет определить масштаб и размеры окружности, на которой находится дуга. Определение угла дуги позволяет корректно вычислить длину хорды, которую нужно найти. Также полезно знать основные геометрические свойства окружностей и треугольников, чтобы применять соответствующие формулы и методы.
Как найти хорду стягивающую дугу в 60 градусов?
Для того чтобы найти хорду, стягивающую дугу в 60 градусов, необходимо использовать тригонометрические функции. Для начала, определите радиус окружности, на которой находится дуга. Затем, используя формулу для нахождения хорды, вычислите ее длину. В данном случае, формула будет выглядеть следующим образом: длина хорды = 2 * радиус * sin(угол/2). Подставьте значения в данную формулу и получите результат.



