В мире математики существует удивительное множество законов и теорем, которые отличаются от основных и установленных правил. Они проникают в самые глубины наших понятий о математике, расширяя границы нашего понимания и преображая общепринятые представления.
Из представленных в этом разделе исключений вы можете погрузиться в привычную математику, пропустив конкретные определения и технические термины, которые часто сложны для восприятия. Вместо этого будут представлены впечатления и особенности уникальных законов и теорем, чтобы показать вам другую сторону науки чисел и формул.
Возможно, вы никогда не слышали о тех законах и теоремах, которые затрагивают различные области математики, такие как геометрия, алгебра или теория вероятностей. И все же они существуют – некоторые из них были открыты совсем недавно, а другим, настоящим камням преткновения для ученых, потребовались годы исследований и наблюдений. Они вызывают интерес и вдохновляют на новые открытия, нередко ставя под сомнение традиционные представления о математике.
Революционные отклонения от основополагающих принципов математики
Некоторые математические концепции исключительными образом отклоняются от установленных законов и теорем, удивляя своей уникальностью. Они представляют собой истории о появлении новых подходов и принципов, которые меняют наше понимание математики и приводят к откровенным сомнениям по поводу прежних правил.
Парадокс Банаха-Тарского Этот парадокс носит поразительное свойство того, что объем конкретного объекта может быть разделен и снова скомпонован таким образом, чтобы получить два полностью идентичных объема объекта. Понять это можно лишь погружаясь в мир теории множеств и нон-линейной математики. |
Центрированные фракталы Фракталы, созданные с использованием математических формул, могут обладать потрясающим свойством – при каждом масштабировании и повороте, они всегда имеют одну и ту же центральную точку. Это отклонение от традиционной математики и приводит к созданию визуально захватывающих изображений. |
Иррациональные числа Иррациональные числа, такие как √2 или π, не могут быть представлены в виде десятичной дроби или отношения двух целых чисел. Они противоречат общепринятому правилу, что любое число можно представить в виде рациональной дроби, и являются фундаментальным компонентом математических отклонений и аномалий. |
Эти революционные отклонения от законов математики открывают новые горизонты и вызывают нас задуматься о границах нашего понимания мира чисел и формул. Их уникальные свойства способны потрясти наши представления о стабильности и единстве математических законов, принося непредсказуемость и необычные результаты.
Закон Бенфорда: примеры числовой неравномерности распределения
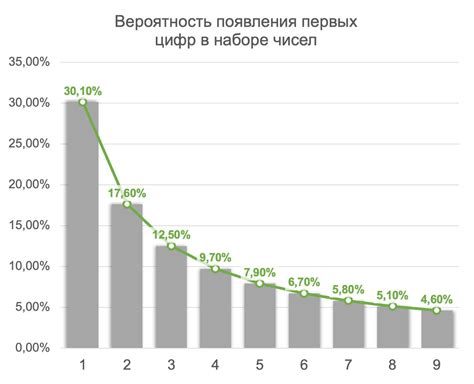
Числа, которые встречаются в нашей повседневной жизни, могут оказаться далеко не такими равномерно распределенными, какими кажутся на первый взгляд. Существует закон, названный в честь американского физика Фрэнка Бенфорда, который зависимость распределения цифр в числах. Закон Бенфорда показывает, что некоторые цифры в числах встречаются значительно чаще, чем другие, противореча общему ожиданию.
Давайте рассмотрим несколько примеров, чтобы лучше понять это явление. Подсчитаем, сколько раз встречается каждая цифра в наборе чисел, представляющих, например, площади всех стран мира. Оказывается, что цифра 1 встречается значительно чаще, чем остальные цифры. По закону Бенфорда, в таком случае, в числах, представляющих площади стран, цифра 1 будет встречаться примерно в 30% случаев, в то время как цифра 9 – всего лишь в 5% случаев.
Еще один интересный пример – распределение первых цифр в числах в различных базах данных. Анализ данных о населении городов, выручке компаний или суммах денег на банковских счетах позволяет заметить, что цифра 1 снова является лидером, встречаясь примерно в 30% случаев. В то же время цифра 9 встречается всего в 5% случаев. Это открытие может быть полезным для обнаружения мошеннических схем, так как некоторые числа, созданные искусственно, не соответствуют закону Бенфорда и могут указывать на манипуляции с данными.
| Цифра | Частота встречаемости (%) |
|---|---|
| 1 | 30 |
| 2 | 17 |
| 3 | 12 |
| 4 | 10 |
| 5 | 8 |
| 6 | 7 |
| 7 | 6 |
| 8 | 5 |
| 9 | 5 |
Закон Бенфорда является примером математического исключения из правил, который показывает, что равномерное распределение чисел не всегда является типичным явлением. Использование этого закона позволяет находить аномалии в данных и обнаруживать мошеннические схемы, основанные на искажении числовых значений. Изучение закона Бенфорда также является интересной областью исследования для математиков, статистиков и специалистов по анализу данных.
Парадокс Монти Холла: подстерегающая ловушка вероятности
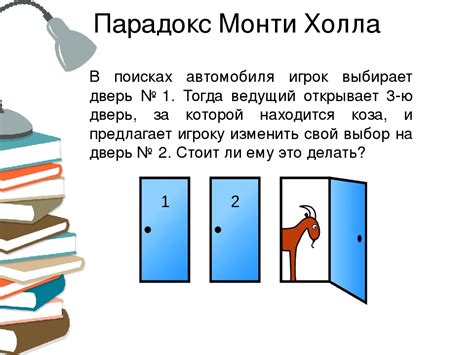
Возможно, каждый из нас сталкивался с ситуацией, когда необходимо сделать выбор из нескольких альтернатив. Представьте себе, что перед вами стоят три закрытых двери, за одной из которых находится ценный приз, а за двумя другими - ничего ценного. Ваша задача состоит в том, чтобы выбрать правильную дверь и выиграть приз.
Стоит отметить, что именно на этом этапе возникает парадокс: последователи Монти Холла утверждают, что вероятность выбора правильной двери существенно изменяется, если в процессе игры предоставляется дополнительная информация.
- На самом деле, при первом выборе вероятность попасть на дверь с призом составляет 1/3.
- Однако, здесь наступает интересный момент: после вашего первоначального выбора ведущий, знающий, где находится приз, открывает одну из оставшихся дверей, за которой нет приза.
- Теперь у вас есть возможность изменить свой выбор и перейти к оставшейся закрытой двери.
- Последователи парадокса утверждают, что вероятность выигрыша при изменении выбора составляет 2/3, в то время как вероятность выигрыша при оставшемся прежнем выборе составляет всего лишь 1/3.
Парадокс Монти Холла вызывает дискуссии и споры среди математиков, так как он противоречит интуиции и повседневному опыту. И хотя кажется, что поменять свой выбор не должно влиять на вероятность выигрыша, математические расчеты доказывают обратное, заставляя нас задуматься о том, насколько изменимы наши убеждения на основе новой информации.
Особенности связи между делимостью и геометрическими представлениями

В данном разделе мы рассмотрим Теорему Безу, которая открывает перед нами новую перспективу на взаимосвязь между делимостью и графиками. Эта теорема позволяет нам установить интересные зависимости между алгебраическими свойствами чисел и их геометрическими представлениями.
Теорема Безу утверждает, что если два многочлена имеют общий корень, то их сумма всегда будет делиться на многочлен, который имеет этот корень. Таким образом, мы можем устанавливать зависимость между делимостью многочленов и характеристиками их графиков.
Теорема Безу имеет далеко идущие практические применения. Она находит своё применение в различных областях, таких как криптография, теория кодирования и конструкции сеток.
Таким образом, изучение Теоремы Безу позволяет нам расширить наши знания о связи между делимостью и геометрическими представлениями. Эта теорема показывает нам, что математика способна устанавливать особые взаимосвязи между различными предметными областями и открывает новые возможности для исследования и понимания мира чисел и форм.
Парадокс произведения: когда произведение равно 1

Обычно мы привыкли, что умножение чисел приводит к увеличению их значения. Но что делать, когда умножение даёт неожиданный результат? Такое происходит, когда одно из умножаемых чисел подчиняется особенному правилу – быть равным 1.
На первый взгляд такое правило может показаться странным. Каким образом произведение может быть равно 1, если один из множителей несет в себе информацию о самом единичном значении? Этот парадокс может показаться нелогичным, но в математике нет места случайностям, и всё имеет свои обоснования и объяснения.
Принимая во внимание постулат о произведении произвольных чисел, оказывается, что когда одно из чисел равно 1, результат умножения всегда будет равен другому числу. При этом, число, равное 1, является нейтральным элементом для операции умножения. Именно благодаря этому можно получить результат, отличный от обычного поведения и ожиданий.
Интересно отметить, что этот парадокс не ограничивается натуральными числами, он распространяется и на другие виды чисел, такие как дроби или действительные числа. Все они подчиняются тому же постулату, позволяющему произведению быть равным 1.
Постулат о произведении произвольных чисел, приводящий к парадоксу равенства 1, является одним из множества интересных аспектов, которые математика предлагает нам изучить. В таких исключениях можно найти удивительные закономерности и расширить наше понимание об основах математического мира.
Законченность множества натуральных чисел: бесконечность не всегда бесконечна

Мы привыкли считать, что множество натуральных чисел не имеет конца и бесконечно увеличивается с каждым последующим числом. Однако, математика нас удивляет: оказывается, что бесконечность не всегда равная бесконечности. Существуют случаи, когда одно множество бесконечно, а другое множество, казалось бы, "меньше", тем не менее имеет такое же количество элементов.
В этом разделе мы рассмотрим концепцию конечных и бесконечных множеств, а также рассмотрим примеры, демонстрирующие, что число элементов множества не всегда определяет его размер. Будет раскрыт принцип равномощности и понятие "счетного множества", которое, несмотря на свою бесконечность, оказывается вполне сравнимым с множеством натуральных чисел.
Парадоксы бесконечности: отрицательная бесконечность и сравнительная бесконечность

Отрицательная бесконечность – понятие, которое вызывает множество вопросов и смущений. Это понятие отличается от традиционного представления о бесконечности, которое часто связывается с положительными числами. Бесконечность в отрицательном направлении представляет собой интересную ситуацию, где числа становятся все более и более малыми за бесконечно большое количество шагов. В этом контексте мы попытаемся разобраться, как отрицательная бесконечность функционирует в математическом мире и как она может быть использована в реальных задачах и моделях.
Сравнительная бесконечность является другим интересным парадоксом, который вызывает недоумение и споры в мире математики. Это понятие связано с тем, что существует несколько разных бесконечностей, которые имеют различные "размеры". Это означает, что некоторые бесконечные множества могут быть больше или меньше других бесконечных множеств. В данном разделе мы рассмотрим эти явления и попытаемся разобраться, как они соотносятся между собой и какое значение они имеют в контексте математических моделей и теорий.
В итоге, изучение парадоксов отрицательной и сравнительной бесконечности позволяет нам расширить наше понимание о числах и их свойствах. Эти парадоксы становятся прекрасным инструментом для анализа и изучения математической реальности за пределами установленных правил и законов. Подробное рассмотрение этих парадоксов поможет нам лучше понять природу бесконечности и ее влияние на наши математические модели и теории.
Парадокс Рассела: возможно ли создать множество, которое исключает само себя?
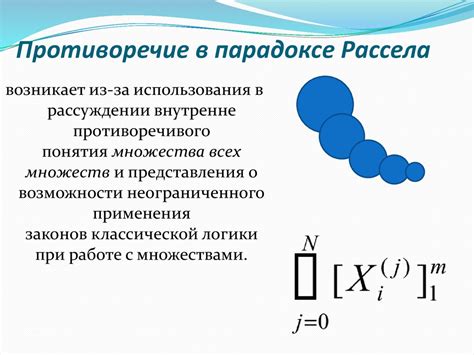
Для демонстрации парадокса Рассела, рассмотрим идею "множество всех множеств, которые не содержат самих себя в качестве элементов". Подробное рассмотрение этого предположения приводит к странной ситуации: если такое множество содержит само себя в качестве элемента, то оно должно быть исключено из самого множества, но в таком случае оно уже не может быть его элементом. Если же оно не содержит само себя в качестве элемента, то оно должно быть включено в множество, как элемент, но тогда оно не соответствует определению множества. В итоге, независимо от того, включено ли множество в себя или исключено из него, возникает противоречие.
| Парадокс Рассела: |
|---|
| Множество всех множеств, которые не содержат самих себя в качестве элементов |
| содержит само себя |
| не содержит само себя |
Такой парадокс отображает важность четкого формулирования и определения в математике и логике. Он также подчеркивает ограничения предметно-категориального подхода и показывает, что существуют явления, которые не могут быть логически объяснены или представлены в рамках привычных правил и законов.
Динамические системы: когда неизменность окружения нарушает математические принципы

В мире математики есть некоторые законы и теоремы, которые считаются абсолютными и неизменными. Однако, существуют сферы, где динамические системы нарушают эти принципы и привносят непредсказуемость в математические модели. Такая ситуация возникает, когда константность окружающей среды становится под вопросом, и математика, изначально основывавшаяся на стабильности, сталкивается с неожиданными явлениями.
Один из примеров такого нарушения математических законов – погода. Вряд ли можно найти человека, который сможет точно предсказать, какой будет погода в определенный день. Несмотря на обширные наблюдения и сбор данных, динамические системы, к которым относится природная среда, остаются непредсказуемыми. Такие системы отклоняются от стандартных математических законов и заставляют ученых постоянно искать новые подходы и модели.
Другим примером является финансовая сфера. Внешние факторы, такие как политические события или экономические кризисы, могут привести к глобальным изменениям в финансовой системе и рынке ценных бумаг. Динамические системы, деятельность которых определяется внешними факторами, вмешиваются в математические модели и создают новые правила, которые не всегда соответствуют общепринятым теоремам.
Природа и финансы – это лишь некоторые примеры динамических систем, которые нарушают математические законы. Возникающая в таких системах непредсказуемость является сложным объектом изучения для математиков, и способы ее моделирования продолжают развиваться. Однако, понимание того, как окружение может воздействовать на математические принципы, помогает нам лучше понять и объяснить множество явлений, которые мы наблюдаем в реальном мире.
| Примеры динамических систем | Влияние окружающей среды |
|---|---|
| Погода | Неопределенность в прогнозировании |
| Финансовая сфера | Непредсказуемость ценных бумаг |
| Биологические системы | Изменение эволюционного развития |
| Социальные системы | Непостоянство поведения людей |
Математическая головоломка: загадка вычислений

Теорема Морлая открывает перед нами дверь в мир математической загадочности. Она представляет собой настоящую головоломку, в которой функция существует и однозначно определена, но невозможно вычислить ее значение точно. Таким образом, мы сталкиваемся с ситуацией, когда математика предлагает нам некий объект, но не обеспечивает нам полной информации о нем.
Теорема Морлая вызывает у нас чувство удивления и мысли о том, насколько глубока и неисчерпаема математика. Она наталкивает нас на мысль о том, что не все в этом мире можно достичь и познать полностью. Возможно, это похоже на мир неразгаданных загадок, где нам постоянно будут встречаться преграды, стимулируя и наш ум и наше воображение.
Таким образом, Теорема Морлая представляет собой интересное исключение из обычных математических правил. Она призывает нас к смирению перед неразгаданными загадками математики и к постоянному стремлению к новым открытиям и познанию. Когда мы вспоминаем о Теореме Морлая, мы понимаем, что математика - это не просто набор формул и правил, но и увлекательное исследование неизвестного.
Вопрос-ответ

Какие законы и теоремы можно отнести к уникальным в математике?
В математике существует множество уникальных законов и теорем, например, теорема Ферма, теорема Пифагора, закон больших чисел и многие другие. Каждая из них имеет свои особенности и применяется в различных областях математики.
Как уникальные законы и теоремы определяются и доказываются?
Определение и доказательство уникальных законов и теорем в математике обычно требует глубокого анализа, логического мышления и применения различных математических методов. Математики проводят исследования, используют леммы, пользуются уже известными теоремами и принципами для создания новых доказательств и определений.
Какова роль уникальных законов и теорем в развитии математики?
Уникальные законы и теоремы являются основой развития математики. Они помогают математикам решать сложные задачи, открывать новые области и подтверждать правильность математических моделей. Эти законы и теоремы позволяют открыть новые закономерности и развивать новые математические направления.
Какие примеры уникальных законов и теорем можно привести в математике?
Примерами уникальных законов и теорем в математике являются теорема Ферма, закон больших чисел, теорема Пифагора, формулы Ньютона-Лейбница и Эйлера, теория вероятностей и много других. Каждая из них имеет свои особенности и применяется в различных областях математики.
Как уникальные законы и теоремы влияют на практическую применимость математики?
Уникальные законы и теоремы в математике обеспечивают практическую применимость этой науки. Они используются в различных областях, таких как физика, экономика, информационные технологии и т.д. Например, закон больших чисел позволяет прогнозировать результаты случайных событий, а теорема Пифагора используется при решении геометрических задач.
Чему посвящена статья "Математика исключения из правил: уникальные законы и теоремы"?
Статья посвящена уникальным законам и теоремам в математике, которые отличаются от общепринятых правил и представляют собой особые исключения.



