Позиционирование центра окружности внутри трапеции - это одно из главных понятий, которые применяются в геометрии для определения и изучения свойств этой фигуры. Наше понимание расположения середины окружности в трапеции играет важную роль в решении различных задач, связанных с этой геометрической фигурой. В этом разделе рассмотрим основные принципы и методы, которые позволят нам достичь глубокого понимания того, как вычислять и визуализировать положение центра окружности внутри трапеции.
Начнем с самых базовых моментов: что такое трапеция? В геометрии трапеция - это фигура, имеющая две параллельные стороны, но не все стороны равны в длине. Одна из самых важных характеристик трапеции - ее основания, которые представляют собой две параллельные стороны. Середина окружности, или центр окружности, является значимым атрибутом, который можно определить внутри границ трапеции.
Что такое центр окружности? Центр окружности - это точка внутри окружности, которая находится на равном расстоянии от всех ее точек. Определение положения центра окружности внутри трапеции является ключевым моментом, который отражает особенности геометрической структуры данной фигуры. Знание точного положения центра окружности внутри трапеции позволяет нам проводить дальнейшие вычисления и анализировать свойства этой геометрической фигуры.
Определение геометрического центра трапеции
Геометрический центр трапеции определяется как точка пересечения медиан, проведенных из середин оснований. То есть, если мы возьмем середины оснований трапеции - точки, где делится основание пополам, и соединим их медианами, то их пересечение будет точкой, которая является геометрическим центром трапеции.
Геометрический центр трапеции имеет свойства, которые делают его важным элементом в положении фигуры. Он равноудален от всех вершин трапеции, а также делит отрезки между вершинами и серединами оснований на две равные части. Это свойство позволяет использовать геометрический центр трапеции для определения различных параметров и построения геометрических конструкций.
Определение геометрического центра трапеции является важным шагом в изучении и понимании данной геометрической фигуры. Знание положения и свойств геометрического центра позволяет решать задачи и проводить различные конструкции, связанные с трапецией.
- Геометрический центр трапеции находится в точке пересечения медиан.
- Геометрический центр равноудален от всех вершин трапеции.
- Геометрический центр делит каждое из оснований на две равные части.
- Геометрический центр трапеции используется для решения задач и построения геометрических конструкций.
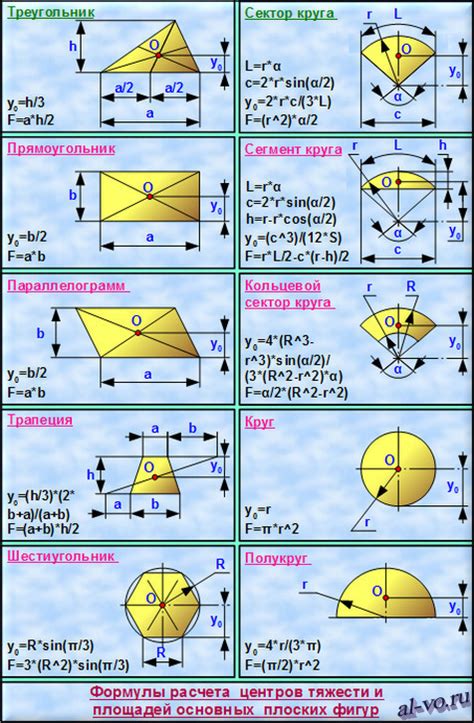
Формула вычисления положения центра вписанной окружности в трапецию
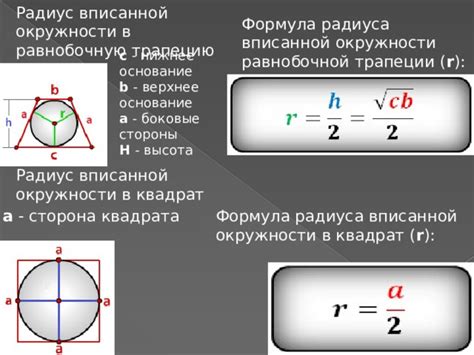
В данном разделе рассмотрим метод определения координат центра окружности, вписанной в трапецию. Этот метод позволяет вычислять точное положение центра окружности без необходимости знать другие параметры фигуры.
Для того чтобы найти центр вписанной окружности в трапецию, используются основные свойства геометрической фигуры. Основной идеей является нахождение точки пересечения двух диагоналей трапеции.
Представим себе трапецию как таблицу, где строками выступают ее стороны, а столбцами - ее вершины. Одна из сторон обозначается как основание, а другая - как верхнее основание. Затем, используя значения координат точек, можно построить уравнения прямых, которые образуют диагонали трапеции.
Для найденных уравнений прямых используется метод решения системы уравнений, позволяющий найти точку пересечения диагоналей. Координаты этой точки и являются координатами центра вписанной окружности в трапецию.
Таким образом, для определения положения центра вписанной окружности в трапецию не требуется знание других параметров фигуры. Данная формула является универсальным инструментом для нахождения положения окружности в трапеции и может быть применена в различных геометрических задачах.
| Разделы | Темы |
| Местоположение | Центра окружности в трапеции |
| Формула | Вычисления положения центра вписанной окружности |
| Метод | Определения координат центра окружности |
Геометрическое объяснение ориентации центра окружности в трапеции

Размещение центра окружности в трапеции может быть объяснено геометрическими принципами и относительным расположением элементов фигуры. Рассмотрение такого размещения требует анализа поведения окружности и ее связи с сторонами и диагоналями трапеции.
- Взаимное положение диагоналей трапеции. Если диагонали трапеции пересекаются, то центр окружности будет находиться внутри трапеции. Если же диагонали параллельны, то центр окружности будет находиться вне фигуры.
- Взаимное положение сторон трапеции. Если стороны трапеции пересекаются в точке, то центр окружности может находиться как внутри фигуры, так и на ее границе.
- Соотношение между радиусом окружности и высотой трапеции. Чем больше радиус окружности, тем ближе центр окружности будет к центру трапеции.
Исходя из этих геометрических факторов, можно определить вероятное расположение центра окружности в трапеции. Однако, необходимо учитывать и другие факторы, такие как отношение длин сторон, углы и размеры трапеции, чтобы получить более точный результат.
Расположение окружностей в прямоугольной и равнобедренной трапеции
В данном разделе рассмотрим, каким образом могут располагаться окружности в прямоугольной и равнобедренной трапеции. Изучение этого вопроса позволит нам более глубоко понять геометрические свойства трапеции и связанных с ней фигур.
- Расположение окружностей в прямоугольной трапеции:
- Когда верхняя и нижняя стороны прямоугольной трапеции являются параллельными и равными, окружность может быть описана вокруг трапеции. Центр этой окружности будет лежать на пересечении диагоналей трапеции.
- Также, в прямоугольной трапеции возможно наличие вписанной окружности, которая касается всех четырех сторон. Центр этой окружности будет лежать на пересечении высот трапеции.
- Расположение окружностей в равнобедренной трапеции:
- В равнобедренной трапеции также может быть описана окружность, проходящая через все вершины фигуры. Центр этой окружности находится в центре основания трапеции, на одном из ее отрезков.
- Также в равнобедренной трапеции можно найти вписанную окружность, которая касается всех сторон фигуры. Центр этой окружности будет лежать на высоте, проведенной из вершины трапеции в основание.
Изучение указанных случаев расположения окружностей в прямоугольной и равнобедренной трапеции позволяет лучше понять особенности этих фигур и их взаимосвязь с окружностями. Это важно для дальнейшего изучения геометрии и применения ее в практических задачах.
Зависимость расположения середины окружности от характеристик фигуры

В данном разделе мы рассмотрим, как изменяется положение середины окружности, центр которой лежит на прямой, относительно параметров трапеции. Рассмотрение данной зависимости позволит нам лучше понять, как фигура выглядит и как она взаимодействует с окружностью.
1. Зависимость от угла наклона сторон
Первым фактором, который будет влиять на положение середины окружности, является угол наклона сторон трапеции. Если угол наклона больше, то середина окружности будет смещаться в одну сторону, если угол наклона меньше - в другую. Угол наклона может меняться от горизонтального положения, при котором трапеция является прямоугольной, до вертикального, при котором одна из сторон трапеции становится бесконечно длинной.
Пример: Если трапеция имеет угол наклона вправо, то середина окружности будет смещаться вправо. Если угол наклона влево, середина окружности будет смещаться влево.
2. Зависимость от высоты трапеции
Высота трапеции также оказывает влияние на положение середины окружности. Чем выше трапеция, тем дальше от основания она будет находиться и тем ближе середина окружности будет к верхней границе трапеции. Это связано с тем, что высота определяет расстояние от основания до вершины, вокруг которой окружность будет строиться.
Пример: Если трапеция имеет большую высоту, то середина окружности будет ближе к верхней границе трапеции. Если высота маленькая, середина окружности будет ближе к основанию.
3. Зависимость от длин сторон трапеции
Длины сторон трапеции также влияют на положение середины окружности. Чем больше длина одной из сторон, тем больше окружность будет отдалена от этой стороны. Часть трапеции, которая находится ближе к более короткой стороне, оказывает большее влияние на положение середины окружности.
Пример: Если одна сторона трапеции длиннее, то окружность будет находиться ближе к более короткой стороне. Если стороны равны по длине, то середина окружности будет находиться на середине между ними.
Таким образом, исходя из угла наклона сторон, высоты и длин сторон трапеции можно предсказать положение середины окружности, что позволит нам лучше визуализировать и анализировать данную геометрическую фигуру.
Разнообразные ситуации: вычисление центра окружности в разных трапециях
В этом разделе мы рассмотрим несколько примеров, где мы можем определить местоположение центра окружности в различных фигурах, которые имеют форму трапеции. Решение этих задач позволяет нам лучше понять, как устроены эти геометрические фигуры и развивать нашу интуицию относительно их свойств.
В первом примере рассмотрим трапецию, в которой боковые стороны параллельны, а основания различны по длине. Наша задача - найти центр окружности, вписанной в эту трапецию. Такие ситуации часто встречаются в реальных жизненных задачах, где нам необходимо рассчитать различные параметры конструкций или объектов.
Во втором примере рассмотрим симметричную трапецию, где все стороны равны, но углы между сторонами могут быть разными. В этом случае также требуется определить положение центра окружности, чтобы применить это знание в различных инженерных расчетах или архитектурных конструкциях.
В третьем примере рассмотрим частный случай трапеции, где одно из оснований является диаметром окружности, вписанной внутрь трапеции. Узнаем, где находится центр окружности в такой фигуре и какие практические применения могут быть связаны с этой информацией.
Разберем эти примеры подробно, приведем математические выкладки и объяснения, чтобы лучше понять процесс определения местоположения центра окружности в разных трапециях. Это поможет нам укрепить наши знания и умения в области геометрии и практического применения этих знаний.
Лемма о среднем перпендикуляре в трапеции

Для доказательства леммы рассмотрим произвольную трапецию и обозначим ее вершины как А, В, С и D. С помощью геометрических построений и выкладок мы покажем, что точка пересечения диагоналей трапеции является центром окружности, описанной около этой фигуры. Далее мы выведем формулу для определения координат этой точки в зависимости от координат вершин трапеции.
Лемма о среднем перпендикуляре в трапеции является важным инструментом в геометрии. Ее применение позволяет находить центр окружности, описанной вокруг трапеции, без необходимости знать все стороны и углы фигуры. Это значительно упрощает геометрические вычисления и аналитическую геометрию.
| Преимущества леммы: | Применение леммы: |
| 1. Упрощение геометрических вычислений. | 1. Определение центра окружности, описанной около трапеции. |
| 2. Использование координатной геометрии для нахождения центра окружности. | 2. Решение задач, связанных с трапециями и окружностями. |
| 3. Прецизионное определение центра окружности. | 3. Создание геометрических построений с использованием леммы. |
Свойства геометрического центра фигуры внутри многоугольника

В этом разделе рассмотрим общие свойства геометрического центра, находящегося внутри многоугольника, который выглядит как трапеция.
Мы изучим особенности расположения и взаимодействия этого центра с другими элементами фигуры, не углубляясь в точные математические определения.
Практическое применение понимания расположения главного круга внутри пятиугольной фигуры трапеции
Разумение позиции главного кружка, занимающего центральную точку внутри пятиугольной формы трапеции, имеет ряд практических применений на различных областях деятельности. Знание расположения этой центральной точки позволяет решать разнообразные задачи и создавать оптимальные решения.
Например, в архитектуре и дизайне, понимание расположения главного кружка помогает определить оптимальные размеры и пропорции объектов, таких как круглые окна и выступающие элементы. Знание позиции этой точки также может быть применено в инженерных расчетах, при проектировании вращающихся механизмов и опорных структур, чтобы достичь баланса и устойчивости системы.
В области геодезии и картографии, знание местоположения центра окружности трапеции позволяет определить точку начала и конца контуров, а также помогает вычислять площади различных географических областей. Это знание может быть полезным также в наблюдательных исследованиях при определении местоположения объектов на поверхности Земли.
Не только в науке и технологии, но и в других сферах жизни, понимание расположения главного кружка трапеции может быть полезным. Например, в математическом образовании, знание этой точки и ее связи с другими элементами помогает студентам углубить свое понимание геометрии и развить логическое мышление. И даже в повседневной жизни, это знание может помочь при планировании интерьера или создании произведений искусства, добавляя в них гармонию и эстетическую привлекательность.
Итак, понимание местоположения главного кружка внутри трапеции имеет широкое практическое значение в различных областях и деятельности, оно помогает решать задачи, создавать оптимальные решения и достигать гармонии в разных аспектах нашей жизни и окружающего мира.
Вопрос-ответ

Как определить местоположение центра окружности в трапеции?
Местоположение центра окружности в трапеции можно определить следующим образом: проведите диагональ трапеции, соединяющую основания, найдите её середину. От середины диагонали проведите перпендикуляр к боковой стороне трапеции. Точка пересечения перпендикуляра и боковой стороны будет являться центром окружности.
Как использовать местоположение центра окружности в трапеции на практике?
Местоположение центра окружности в трапеции полезно использовать при решении геометрических задач, связанных с окружностями. Например, при нахождении радиуса окружности, вписанной в трапецию, или при нахождении длины хорды окружности, проходящей через центр трапеции.
Как можно доказать, что указанная точка является центром окружности в трапеции?
Чтобы доказать, что указанная точка является центром окружности в трапеции, можно воспользоваться свойствами окружностей и равенствами треугольников. Например, можно доказать, что расстояние от центра окружности до каждой из вершин трапеции равно, или что углы между радиусами, проведенными из центра к вершинам трапеции, также равны.
Какие могут быть специальные случаи при местоположении центра окружности в трапеции?
В зависимости от свойств и формы трапеции, местоположение центра окружности может иметь различные специальные случаи. Например, если трапеция является прямоугольной, то центр окружности будет совпадать с центром окружности, вписанной в прямоугольник. Также местоположение центра окружности может быть определено с помощью других геометрических свойств трапеции.
Можно ли использовать знание местоположения центра окружности в трапеции для вычисления других характеристик фигуры?
Да, знание местоположения центра окружности в трапеции может быть полезным для вычисления других характеристик фигуры. Например, с помощью центра окружности можно вычислить площадь фигуры, либо выяснить, является ли данная трапеция трапецией Паскаля.
Как определить местоположение центра окружности в трапеции?
Местоположение центра окружности в трапеции можно определить с помощью специальной формулы. Для этого необходимо знать длины базы трапеции и одной из боковых сторон. Центр окружности будет располагаться на пересечении двух перпендикуляров, проведенных к серединам боковых сторон трапеции.



