Ориентируясь на глубокую математическую аналогию, мы можем погрузиться в изучение области, связанной с местоположением и интригующими свойствами перекрестного пункта, формируемого средними перпендикулярами, присущими экстремальным треугольникам. В дальнейшем в нашем исследовании мы предлагаем аккуратно концептуализировать и описать эти критические признаки без использования общих определений.
Когда мы обращаем своё внимание на данный предмет, становится очевидным, что этот обобщенный случай безусловно заслуживает внимания наших интеллектуальных устремлений в предмете геометрии. Внутри данного контекста мы стремимся достичь полного исследования характеристик, связанных с точкой взаимного пересечения, используя наши умственные способности и логические аргументы.
В дополнение к этому, мы попытаемся избегать пошагового описания видов точек пересечения серединных перпендикуляров, поскольку наша цель - продемонстрировать всю глубину и значимость данной проблематики. Мы будем стремиться к переосмыслению, истолкованию и новым понятиям, чтобы воплотить эту уникальную математическую абстракцию в академическом контексте.
Обозначение центра отрезка на плоскости в геометрии
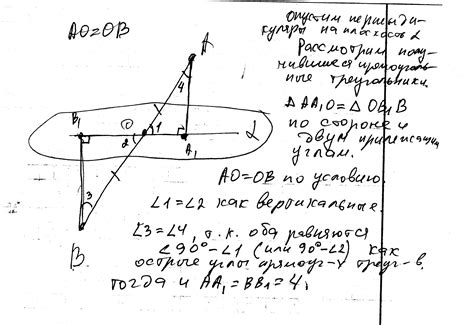
| Символ | Обозначение | Описание |
|---|---|---|
| • | М | Середина отрезка |
Обозначение середины отрезка на плоскости может варьироваться в зависимости от используемых систем координат и конкретного контекста задачи. В некоторых случаях середину отрезка обозначают точкой "М", а в других случаях могут использоваться другие символы, такие как точка ".", "O", "C" и т.д. Важно помнить, что обозначение само по себе не влияет на свойства и характеристики середины отрезка, а служит только для удобства обращения к этой точке в дальнейшем рассмотрении задачи.
Середина отрезка может играть важную роль при построении графиков, вычислении длины отрезка, нахождении координат других точек на отрезке и во множестве других геометрических операций и задач. Знание понятия и свойств середины отрезка помогает более точно и эффективно решать геометрические задачи и проводить доказательства с использованием этой важной точки на плоскости.
Определение и способы нахождения середины отрезка

Существует несколько способов нахождения середины отрезка. Один из них - это использование формулы координат. Если известны координаты начальной и конечной точек отрезка, то координаты середины можно найти путем нахождения среднего арифметического их координат. Другой способ - использование масштабных отрезков. Участок, на котором лежит середина, делится на одинаковые части, равные длине отрезка. Также можно построить перпендикуляр к отрезку, затем провести его из концов отрезка и найти точку пересечения.
- Середина отрезка - это точка, равноудаленная от его концов.
- Способы нахождения середины отрезка: с помощью формулы координат, использование масштабных отрезков, построение перпендикуляра.
Острый угол в геометрии треугольника
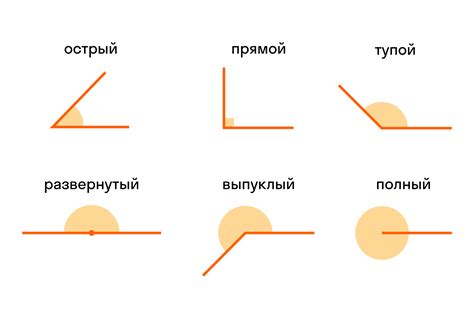
Острые углы играют значимую роль в геометрии треугольника, так как влияют на его геометрические свойства и определяют различные аспекты его конструкции. Понимание этих углов позволяет нам более глубоко изучать структуру треугольника и его основные характеристики.
В данном разделе будут рассмотрены основные особенности острых углов: их взаимное расположение в треугольнике, зависимость от длин сторон, а также связь с другими элементами геометрической фигуры, такими как медианы, биссектрисы и описанные окружности.
| Основные вопросы, рассматриваемые в разделе: | Примеры вопросов |
|---|---|
| Как связаны острые углы с длинами сторон треугольника? | Как зависит величина острого угла от соответствующей стороны? |
| Какое взаимное расположение имеют острые углы? | Как связаны острые углы треугольника между собой? |
| Как острые углы влияют на другие элементы треугольника? | Как острые углы влияют на положение медиан и биссектрис треугольника? |
Изучение свойств острых углов является важным шагом для понимания и анализа треугольников, а также для решения геометрических задач, связанных с ними. Вследствие этого, данный раздел призван сделать нас более компетентными в области анализа и работы с острыми углами в треугольнике.
Острые углы и внешний вид остроугольного треугольника
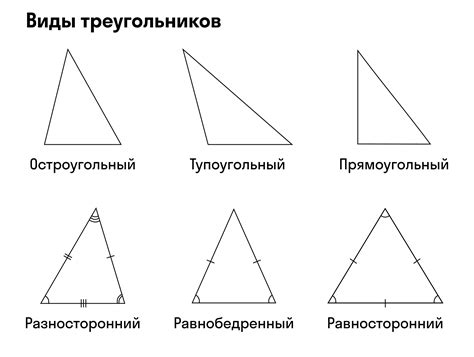
Острые углы оказывают особое влияние на свойства и форму остроугольного треугольника. Эти углы, которые меньше прямого угла (90 градусов), создают особую динамику и гармонию внутри треугольника.
Остроугольный треугольник описывается тремя углами, все из которых являются острыми. Такой треугольник отличается от остальных из-за своего особенного внешнего вида. Все его углы направлены внутрь, формируя острый конечный угол в каждой вершине.
Изображение остроугольного треугольника будет выглядеть следующим образом:
△ABC
Где:
△ - символ, обозначающий треугольник;
A, B и C - точки вершин треугольника.
Описание центральной точки перпендикуляра
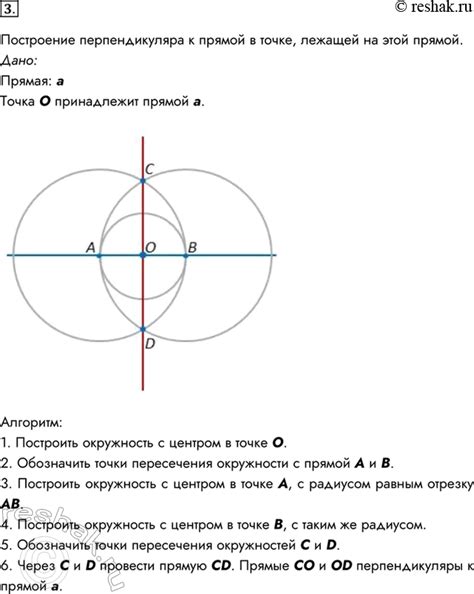
В данном разделе мы рассмотрим центральную точку перпендикуляра остроугольного треугольника. Узнаем основные характеристики этой точки и их взаимосвязь с геометрическими свойствами треугольника.
Центральная точка перпендикуляра представляет собой точку, которая расположена на прямой перпендикулярно oстроугольному треугольнику. Отличительной особенностью этой точки является то, что она находится точно в середине этого перпендикуляра. Благодаря такому расположению центральной точки, острые углы треугольника равны между собой, что придает ему определенное гармоничное соотношение.
| Характеристика | Связь с геометрическими свойствами |
|---|---|
| Расположение | Центральная точка перпендикуляра находится на равном расстоянии от двух точек пересечения серединных линий треугольника. |
| Равенство углов | Острые углы треугольника, образованные с прямыми серединными перпендикулярами, равны между собой. |
| Отношения длин сторон | Длины сторон остроугольного треугольника могут быть выражены через отношение к центральной точке перпендикуляра. |
Центральная точка перпендикуляра играет важную роль в геометрических вычислениях и построениях, позволяя нам более глубоко понять связь между различными геометрическими объектами и характеристиками остроугольных треугольников. Знание о свойствах этой точки помогает в решении задач на практике, а также в дальнейшем изучении геометрии.
Определение и взаимосвязь середины перпендикуляра с точкой их пересечения
Существует способ определения точки пересечения серединных перпендикуляров остроугольного треугольника, а именно путем нахождения середины каждой стороны и соединения найденных середин отрезком. Эта точка, называемая "серединой перпендикуляра", находится внутри треугольника, обладает определенными свойствами и играет важную роль в геометрии.
Середина перпендикуляра представляет собой точку, которая равноудалена от каждого из концов перпендикуляра, она лежит на прямой, проходящей через середины сторон треугольника и перпендикулярна им.
Середина перпендикуляра и точка их пересечения связаны друг с другом, поскольку, в случае остроугольного треугольника, эти точки совпадают. Таким образом, середина перпендикуляра является одновременно точкой пересечения серединных перпендикуляров, что делает ее особенно значимой в изучении форм и свойств треугольников.
Отметка средних прямых, перпендикулярных сторонам, в остроугольном треугольнике
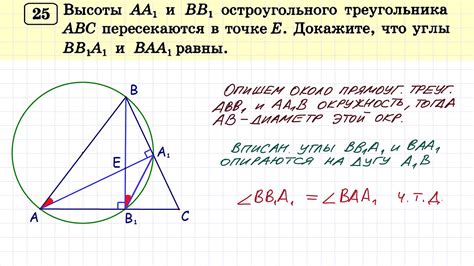
Средние прямые, перпендикулярные сторонам, проходят через середины каждой стороны треугольника. Их отметка вносит определенную симметрию в фигуру, придавая ей особый характер и структуру. Благодаря этим линиям треугольник делится на несколько меньших фигур, каждая из которых имеет определенные свойства.
Средние прямые встречаются в центре треугольника, где образуют точку, называемую центром симметрии. Эта точка является пересечением симметрично расположенных линий и обладает особыми свойствами. Каждая из средних прямых является перпендикуляром к соответствующей стороне треугольника и делит ее пополам.
Зная свойства средних прямых и их отношение к сторонам треугольника, можно провести различные геометрические рассуждения и доказательства. Отметка этих линий помогает в изучении особенностей треугольника и открывает новые перспективы в геометрической анализе.
Как найти середины сторон остроугольного треугольника и построить через них перпендикуляры?

- Найдите середину первой стороны треугольника, соединяющую две его вершины. Для этого можно взять линейку и измерить половину длины стороны, а затем провести от этой точки вертикальную прямую до противоположной стороны треугольника.
- Повторите эту операцию для оставшихся двух сторон треугольника. Найдите середины второй и третьей сторон и проведите через них соответствующие вертикальные прямые.
- В результате вы получите три перпендикуляра, проходящих через середины сторон остроугольного треугольника. Изучите их взаимное расположение и важные свойства.
Построение серединных перпендикуляров не только позволяет нам визуализировать исходный треугольник, но и является важным шагом для дальнейших исследований и решения геометрических задач.
Определение точки пересечения перпендикуляров
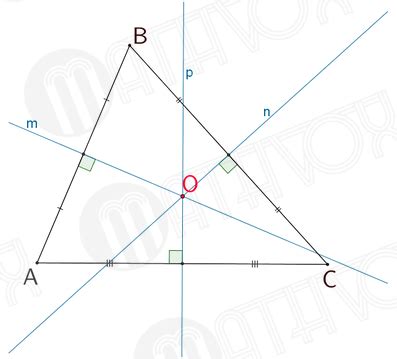
Именно пересечение данных перпендикуляров дает нам эту особенную точку, которая имеет ряд интересных свойств и существенно влияет на геометрические параметры треугольника. Местоположение данной точки зависит от величины сторон треугольника и может быть использовано для решения различных задач геометрии.
Точка пересечения перпендикуляров обычно обозначается буквой "О" и может быть найдена с использованием специальных математических формул и методов. Она служит началом для изучения других важных концепций и закономерностей остроугольных треугольников, а также находит свое применение в практических задачах различных областей науки и техники.
Вопрос-ответ

Каковы свойства точки пересечения серединных перпендикуляров остроугольного треугольника?
Точка пересечения серединных перпендикуляров остроугольного треугольника является его ортоцентром, то есть точкой пересечения его высот. Она также является точкой пересечения симедиан, медиан и радикальной оси вписанной окружности треугольника. Ортоцентр находится на одной третьей от каждой из сторон треугольника.
Как найти местоположение точки пересечения серединных перпендикуляров остроугольного треугольника?
Для нахождения точки пересечения серединных перпендикуляров остроугольного треугольника необходимо найти середины каждой из сторон треугольника и провести перпендикуляры к этим сторонам через соответствующие середины. Точка пересечения этих перпендикуляров будет являться искомой точкой.
Какой геометрический смысл имеет точка пересечения серединных перпендикуляров остроугольного треугольника?
Точка пересечения серединных перпендикуляров остроугольного треугольника обладает несколькими геометрическими свойствами. Она является ортоцентром треугольника - точкой пересечения его высот. Также она является центром окружности, вписанной в треугольник, которая проходит через середины сторон треугольника и центр этой окружности совпадает с ортоцентром. Более того, точка пересечения серединных перпендикуляров также является точкой пересечения симедиан и медиан треугольника.