Когда мы рассматриваем геометрию и анализ на плоскости, мы сталкиваемся с важным понятием - симметрией. Симметрия, как регулярная черта объектов и функций, отражает порядок и гармонию в нашем мире. Она позволяет нам визуально распознавать и понимать различные формы и закономерности. Однако, сама по себе симметрия является абстрактным понятием и требует определения и описания. В этой статье мы рассмотрим одну из наиболее базовых форм симметрии - симметрию относительно начала координат.
Симметрия относительно начала координат - это свойство, когда график функции (геометрический образ) полностью совпадает с перевернутой копией самого себя относительно начала координат. Это означает, что график функции симметричен как относительно оси абсцисс, так и относительно оси ординат. Такая симметрия может проявляться в различных формах и размерах функций - от простейших линейных и квадратичных функций до более сложных тригонометрических, показательных и логарифмических функций.
Открытие и исследование симметрии функций относительно начала координат имеет большое практическое значение в таких областях, как математика, физика, экономика и другие. Знание и использование этой симметрии позволяет нам легче анализировать и решать задачи, связанные с определением поведения функций и их свойств. B одном аспекте он расширяет наши возможности в осуществлении предсказаний и прогнозирования на основе имеющихся данных и закономерностей.
Сущность симметрии относительно начала координат
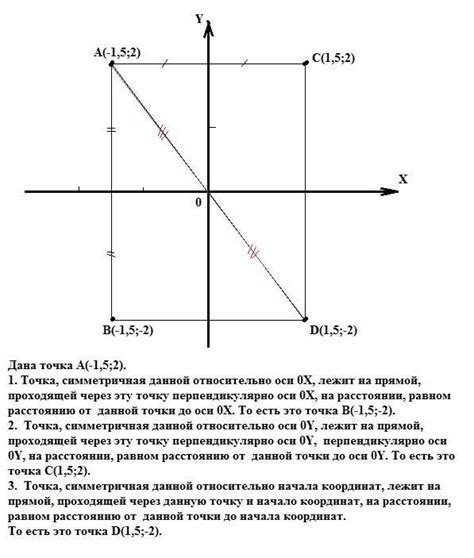
Симметрия относительно начала координат означает, что график функции симметричен относительно оси абсцисс и оси ординат одновременно. Другими словами, если мы проведем линии через начало координат в направлении этих осей, то график функции будет симметрично отражаться вокруг них.
Важно понимать, что симметрия относительно начала координат может иметь различные формы. Например, функция может быть симметричной относительно вертикальной и горизонтальной осей, либо только одной из них. Иногда симметричная функция может иметь особенности, такие как точка перегиба или ось симметрии.
С помощью анализа функции и ее графика мы можем определить, является ли она симметричной относительно начала координат. Для этого нам необходимо проанализировать, совпадают ли значения функции симметрично относительно начала координат и какие формы симметрии она может иметь.
|
|
Графическое определение симметричности функции
В данном разделе мы рассмотрим метод, позволяющий определить симметричность функции относительно начала координат с помощью графика функции. Этот метод основан на визуальном анализе симметрии и позволяет наглядно увидеть свойства функции.
Для начала, следует изучить положительные и отрицательные значения функции на определенном участке графика. Если значения функции симметричны относительно оси ординат, то это может говорить о симметрии функции относительно начала координат.
Также следует обратить внимание на форму графика функции. Если график функции является симметричным относительно осей координат, то это может быть еще одним индикатором симметрии относительно начала координат.
Однако стоит помнить, что графическое определение симметричности функции является приближенным и требует дополнительных проверок с использованием точных математических методов.
Аналитический подход к выявлению симметричности функции

Для определения симметричности функции относительно начала координат необходимо приравнять значение функции в точке (-x, -y) к значению функции в точке (x, y). Если это равенство выполняется для всех точек функции, то функция симметрична относительно начала координат.
Один из способов аналитического определения симметричности функции - это проверка симметричности ее алгебраического выражения. Для этого необходимо заменить переменные в выражении на их противоположные значения и сравнить полученное выражение со исходным. Если полученное выражение эквивалентно исходному, то функция симметрична.
Другой метод аналитического определения симметричности функции - это использование аналитических свойств симметричных функций. Например, если функция является четной, то она симметрична относительно оси ординат, то есть f(-x) = f(x). Если функция является нечетной, то она симметрична относительно начала координат, то есть f(-x) = -f(x).
Аналитический подход к определению симметричности функции относительно начала координат позволяет получить точные и эффективные результаты. Важно учитывать особенности функции и использовать соответствующие методы для ее анализа.
Особенности симметричных функций

В данном разделе мы рассмотрим некоторые интересные особенности, присущие функциям, обладающим симметрией относительно начала координат. Такие функции могут демонстрировать удивительные свойства и геометрические закономерности.
Одной из особенностей является равенство значений функции в точках, симметричных относительно начала координат. Также отметим, что у таких функций графики могут быть зеркально симметричными относительно осей координат.
Интересно, что некоторые симметричные функции обладают свойством сохранения знака. Это означает, что если значение функции положительно (отрицательно) в определенной точке, то оно будет положительным (отрицательным) в симметричной ей относительно начала координат. Такое свойство часто используется при анализе графиков функций.
- Уравнение четной функции может быть записано в виде f(x) = f(-x).
- График нечетной функции всегда симметричен относительно начала координат.
- Существоуют симметричные функции, заданные с помощью тригонометрических функций, экспоненты или логарифма.
- Симметричные функции могут иметь точки перегиба или экстремумы симметрично относительно начала координат.
- Применение преобразования замены переменной позволяет упростить анализ симметричных функций.
Примеры функций, симметричных относительно начала координат
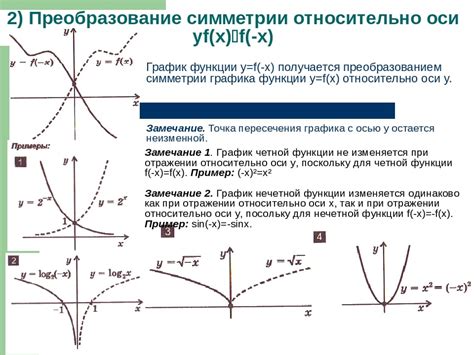
В данном разделе представлены несколько примеров функций, которые обладают симметричностью относительно начала координат. Эта особенность функций означает, что они одинаково выглядят, если отобразить их относительно начала координат.
Первым примером является функция параболы. При работе с данной функцией, можно заметить, что она обладает осевой симметрией относительно вертикальной прямой, проходящей через начало координат. Это означает, что при отражении левой части графика относительно оси ординат, получаем правую часть графика, которая полностью совпадает с оригинальным графиком.
Другим примером функции, обладающей симметричностью относительно начала координат, является функция экспоненты. В данном случае, график функции отображается одинаково относительно оси ординат и абсцисс. Верхняя правая часть графика полностью совпадает с нижней левой, что говорит о наличии осевой симметрии относительно начала координат.
Практическое применение симметрии функций в математике
Одним из практических применений симметрии функций является нахождение экономических и финансовых равновесий. Симметричные функции могут помочь в анализе неопределенности и прогнозировании финансовых результатов. Например, симметричность функций возможна в задачах определения равновесного уровня производства и спроса на рынке.
В графическом дизайне также часто используется симметрия функций для создания эстетически приятных и сбалансированных композиций. Проектировщики и художники используют симметрию функций для создания гармоничного визуального опыта и уравновешивания изображений.
Еще одним примером практического применения симметрии функций является в области физики и инженерии. В механике симметрия функций позволяет упростить решение дифференциальных уравнений и анализировать движение тел. Например, симметрия функции относительно оси X может означать отсутствие горизонтальных сил или моментов на тело.
- Экономика и финансы
- Графический дизайн
- Физика и инженерия
Применение симметрии функций в этих и других областях позволяет более глубоко понять и анализировать различные явления и является важным инструментом для развития научных исследований, технологий и творческих процессов.
Вопрос-ответ

Что такое симметрия функции относительно начала координат?
Симметрия функции относительно начала координат означает, что график функции можно разделить на две части путем его отражения относительно начала координат таким образом, что одна часть графика точно совпадает с другой.
Как можно определить симметричность функции относительно начала координат без построения графика?
Функция является симметричной относительно начала координат, если при замене всех значений переменных на противоположные, значение функции остается неизменным. То есть, если для любого значения x выполняется условие f(x) = f(-x), то функция симметрична относительно начала координат.
Как можно определить симметричность функции относительно начала координат по ее уравнению?
Если уравнение функции f(x) при замене x на -x остается неизменным (т.е. становится равным уравнению f(-x)), то функция является симметричной относительно начала координат.
Какую пользу можно извлечь из знания о симметричности функции относительно начала координат?
Знание о симметричности функции относительно начала координат может быть полезным при построении графика функции. Оно помогает определить симметричные точки относительно начала координат, что в свою очередь может упростить анализ и понимание поведения функции.





