Одной из ключевых задач в математике является изучение зависимостей между различными величинами. Чтобы понять, как одна величина меняется в зависимости от другой, мы часто проводим графический анализ. Один из самых распространенных типов зависимости является линейная функция, которая описывается уравнением у = kх + b.
Коэффициент k в этом уравнении играет особую роль - он определяет наклон графика линейной функции. Понимание значения коэффициента k позволяет нам сделать предсказания о том, как будет изменяться значение у при изменении х. В данной статье мы рассмотрим методы нахождения коэффициента k по графику и узнаем, как интерпретировать его значение в контексте изучаемой зависимости.
Основным методом нахождения коэффициента k является анализ графика линейной функции. Мы можем наблюдать, что каждая точка на графике лежит на одной и той же прямой. Наша задача заключается в том, чтобы определить наклон этой прямой, то есть значение коэффициента k. Существует несколько подходов к решению этой задачи, и мы рассмотрим несколько из них в данной статье.
Определение наклона прямой через график: эффективные пути и подходы
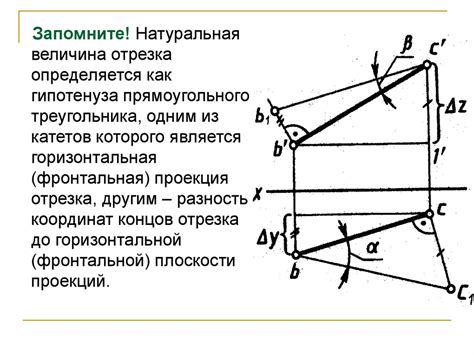
В данном разделе мы рассмотрим различные способы нахождения наклона прямой, основываясь на графическом представлении линейной зависимости между переменными. Будут представлены несколько методик, позволяющих эффективно определить коэффициент наклона (k) при известном уравнении y=kx+b, обратившись к графику.
- Метод касательных точек
- Метод использования изменения координат
- Метод перпендикуляра
Этот метод основывается на выборе двух точек на графике и построении касательной, проходящей через эти точки. Затем измеряется угол наклона касательной. С учетом того, что наклон касательной совпадает с наклоном прямой, можно определить значение коэффициента k.
Этот метод предполагает изменение координат точек на графике с сохранением отношения между ними. Затем находится отношение изменений значений по оси y к изменениям значений по оси x. Полученное отношение является коэффициентом наклона прямой.
В данном методе мы строим перпендикуляр к отрезку прямой, соединяющему две выбранные точки на графике. Затем измеряется угол наклона перпендикуляра. Учитывая, что наклон перпендикуляра равен противоположному по знаку наклону прямой, можно определить значение коэффициента k.
Выбор наиболее подходящего метода зависит от конкретной ситуации и доступных данных. Использование этих методик позволяет определить коэффициент наклона прямой с высокой точностью, используя графическое представление линейной зависимости.
Измерение точек графика и расчет углового коэффициента
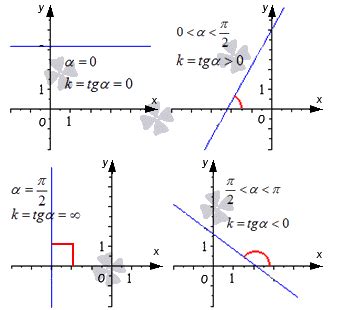
Для измерения точек на графике необходимо использовать координатную сетку. Одна ось графика представляет значения независимой переменной, а другая ось представляет значения зависимой переменной. Путем определения координат точек на графике мы можем провести расчет углового коэффициента.
Угловой коэффициент представляет собой отношение изменения зависимой переменной к изменению независимой переменной. Для его расчета необходимо выбрать две точки на графике и найти разность значений на оси зависимой переменной и оси независимой переменной. Затем, необходимо разделить полученное значение изменения по оси зависимой переменной на значение изменения по оси независимой переменной. Результат этого расчета будет являться угловым коэффициентом и отражать скорость изменения зависимой переменной при изменении независимой переменной.
| Точка на графике | Значение по оси независимой переменной | Значение по оси зависимой переменной |
|---|---|---|
| Точка 1 | x1 | y1 |
| Точка 2 | x2 | y2 |
Угловой коэффициент k вычисляется по следующей формуле:
k = (y2 - y1) / (x2 - x1)
Графический подход к определению наклона прямой
Определение коэффициента наклона линейной функции не всегда требует сложных математических вычислений. Существует графический метод, который позволяет сравнительно легко и наглядно определить этот коэффициент по графику функции.
Графический подход основан на изучении наклона прямой, заданной линейной функцией. Коэффициент наклона k отражает, насколько быстро изменяется значение функции y при изменении значения аргумента x. Чем больше значение k, тем более крутая (стрмая) будет прямая, и наоборот.
Для определения коэффициента наклона можно использовать направляющие векторы. Они позволяют наглядно представить, как изменяются значения x и y при движении по прямой. Чем больше значение y вектора, тем больше значение k.
Другой способ - использование двух произвольных точек на прямой. Измерив изменение значений y и x между этими точками, можно вычислить приближенное значение k. Чем дальше от начала координат расположены точки, тем более точное значение k можно получить.
Используя графический метод, можно сравнивать наклоны разных линейных функций, а также определять тенденции и взаимосвязи между значениями x и y. Это полезный инструмент для анализа данных и прогнозирования.
Итак, графический подход к определению коэффициента наклона линейной функции позволяет визуально и интуитивно понять, как изменяются значения функции при изменении аргумента. Умение работать с графиками поможет лучше понять и использовать линейные функции в реальных задачах.
Аппроксимация данных и определение показателя наклона в уравнении прямой
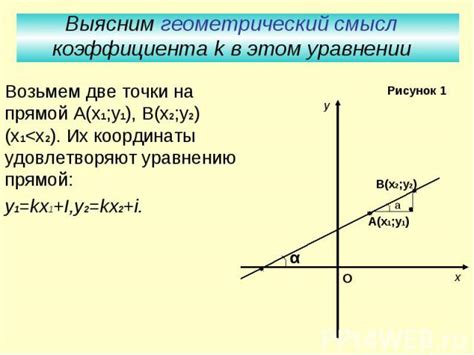
Одним из наиболее распространенных методов для определения показателя наклона является аппроксимация данных. В этом методе мы пытаемся найти наилучшую прямую, которая наиболее точно описывает имеющиеся данные. Аппроксимация данных основана на минимизации отклонений между наблюдаемыми значениями и значениями, которые предсказывает линейная модель.
Для проведения аппроксимации данных можно использовать различные методы, включая метод наименьших квадратов и метод аккуратных находок. Метод наименьших квадратов позволяет найти параметры прямой, минимизируя сумму квадратов разностей показанных и наблюдаемых значений. Метод аккуратных находок основан на выборе двух точек на графике и расчете показателя наклона по формуле.
- Метод наименьших квадратов: нахождение показателя наклона через минимизацию суммы квадратов отклонений
- Метод аккуратных находок: определение показателя наклона по формуле, используя две точки на графике
Какой метод использовать зависит от предпочтений и доступности математических инструментов. Оба метода позволяют получить значение показателя наклона с определенной точностью, что дает возможность более детального анализа данных и проведения прогнозов.
Вопрос-ответ

Как найти коэффициент k в линейной функции через график?
Чтобы найти коэффициент k в линейной функции y=kx+b через график, необходимо выбрать две точки на графике и использовать их координаты для вычисления значения k. Для этого можно взять любые две точки на графике: одну точку помечаем как (x₁, y₁), а другую как (x₂, y₂). Затем, используя формулу k = (y₂ - y₁) / (x₂ - x₁), подставляем значения координат в формулу и рассчитываем коэффициент k.
Какие методы можно использовать для нахождения коэффициента k по графику?
Для нахождения коэффициента k по графику можно использовать несколько методов. Один из них - метод углового коэффициента. Он основан на использовании двух точек на графике и вычислении изменения y и x между этими точками. Коэффициент k равен отношению изменения y к изменению x. Другой метод - метод наименьших квадратов. Он основан на минимизации суммы квадратов отклонений значений y на графике от теоретических значений, которые даются функцией y=kx+b. Коэффициент k можно найти, используя математические вычисления и оптимизацию.
Что означает коэффициент k в линейной функции y=kx+b?
Коэффициент k в линейной функции y=kx+b называется угловым коэффициентом или коэффициентом наклона. Он определяет, насколько быстро растет или убывает значение y в зависимости от изменения значений x. Положительное значение k указывает на положительную зависимость между x и y (увеличение x приводит к увеличению y), а отрицательное значение k - на отрицательную зависимость (увеличение x приводит к убыванию y). Чем больше значение k, тем круче наклон графика функции, а чем меньше значение k, тем более пологий наклон.
Как можно найти значение коэффициента k в линейной функции, используя график?
Для нахождения коэффициента k по графику линейной функции необходимо выбрать две точки на этом графике. Затем нужно вычислить разность между значениями y в этих двух точках и разность между соответствующими значениями x. Затем найденные значения нужно поделить друг на друга, чтобы получить значение коэффициента k.
Какие методы можно использовать для определения коэффициента k в линейной функции, используя график?
Существует несколько методов определения коэффициента k по графику линейной функции. Один из них - метод точек. Он заключается в выборе двух точек на графике и вычислении соотношения изменения значения y к изменению значения x между этими точками. Другой метод - метод изображения графика функции в координатной плоскости и проведения прямой линии, проходящей через точки графика. Третий метод - метод наименьших квадратов, при котором подбирается прямая линия, наилучшим образом аппроксимирующая набор данных на графике. Эти методы позволяют определить значение коэффициента k с высокой точностью.



