В данной статье будут рассмотрены особенности функции с линейным графиком, представленным формулой y = 3x + 1. Изучение данной функции позволит нам погрузиться в мир математических моделей и ближе познакомиться с обратимостью и основными свойствами этой функции.
Основной целью анализа является понимание принципа обратимости – возможности однозначного восстановления аргумента x при известном значении функции y. Именно обратимость функции является одним из ключевых свойств, которое отличает и определяет ее уникальность и практическую значимость.
Для того чтобы более всесторонне изучить эту функцию, в данной статье будут рассмотрены различные аспекты ее поведения: некоторые особенности графика, зависимость от коэффициентов и возможные модификации. Вы сможете увидеть, какие изменения происходят в графике при изменении значений коэффициентов 3 и 1 и как они влияют на обратимость функции.
Что такое функция с линейным уравнением y=3x+1 и как ее определить?

Итак, что означает данное уравнение? Здесь мы имеем дело с прямой линией, представленной на координатной плоскости. Коэффициент при переменной x равен 3, что означает, что за каждое изменение x на единицу, значение y меняется на 3 единицы. Константа +1 обозначает, что прямая пересекает ось y в точке с координатами (0, 1).
Для определения функции с линейным уравнением y=3x+1 необходимо знать значения переменной x и применить их в данное уравнение. Таким образом, для каждого значения x мы можем определить соответствующее значение y. Например, если x=2, то y будет равно 3*2+1=7.
В рассматриваемой функции присутствуют различные свойства, которые могут быть изучены более подробно. Среди них можно выделить такие как: угловой коэффициент, который определяет наклон прямой; смещение по оси y, которое задает точку пересечения с ординатой; область определения и область значений функции. В следующих разделах мы более детально рассмотрим эти и другие свойства функции y=3x+1.
О Диапазоне Возможных Значений и Множестве Определения Функции

В данном разделе рассматривается область действия и множество значений функции, представленной в виде y = 3x + 1. Мы исследуем набор допустимых значениях для переменной x, которые могут использоваться при вычислении функции, а также все возможные результаты, которые могут быть получены после применения заданного правила. При этом мы используем аналогии без упоминания конкретной функции, чтобы представить общий контекст и концепцию.
Один из ключевых аспектов, который нужно уяснить при анализе функции, является множество возможных значений или, другими словами, диапазон значений функции. Это означает, что для каждого допустимого значения переменной x, все значения y, которые могут быть получены после подстановки этого значения в выражение 3x + 1, представляют собой множество значений функции.
| Множество Значений x | Множество Значений y |
|---|---|
| Все действительные числа | Все действительные числа |
Таким образом, область определения функции y = 3x + 1 является множеством всех действительных чисел, а множество значений функции также является множеством всех действительных чисел. Это означает, что функция может быть определена и имеет значение для любого входного аргумента x, который является действительным числом.
Интерпретация графика функции y=3x+1
График функции y=3x+1:
Погрузимся в визуальное представление функции y=3x+1 и рассмотрим его интерпретацию. График функции представляет собой линию на плоскости с осями x и y.
Начнем с рассмотрения коэффициента при x, равного 3. Это означает, что каждый значок на оси x соответствует перемещению на 3 значка на оси y. Это положительный коэффициент, поэтому линия имеет положительный наклон.
Также, уравнение функции содержит константу 1, которая добавляется к значению 3x. Это означает, что график функции будет сдвинут вверх на 1 единицу по оси y.
Итак, визуально интерпретируя график функции y=3x+1, мы видим, что он представляет собой прямую линию с положительным наклоном и сдвигом вверх на 1 единицу. Каждое изменение по оси x приводит к изменению по оси y в соответствии с уравнением функции.
Монотонность и четность функции y=3x+1
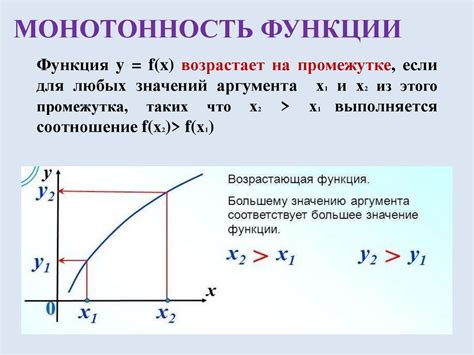
Рассмотрим свойства функции y=3x+1, которые позволяют нам более глубоко понять ее поведение и особенности. В данном разделе мы сосредоточимся на монотонности и четности данной функции.
Монотонность функции описывает ее рост или убывание на определенном интервале. В случае функции y=3x+1 можно сказать, что она является монотонно возрастающей. Это означает, что с увеличением значения переменной x значение функции также возрастает. Однако, стоит отметить, что данная функция не является строго монотонной на всей числовой прямой, так как имеет наклонную прямую.
Четность функции отражает симметричность ее графика относительно оси ординат. В нашем случае функция y=3x+1 является нечетной, так как при замене значения переменной x на -x, знак функции меняется на противоположный. Другими словами, график функции симметричен относительно начала координат.
Обратимость функции y=3x+1 и ее обратная функция
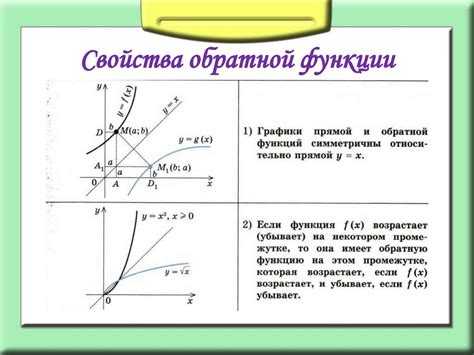
Для исследования обратимости функции y=3x+1 необходимо найти ее обратную функцию. Обратная функция f⁻¹(x) - это функция, которая при подстановке значения x дает значение, равное y оригинальной функции. В данном случае, нам необходимо найти такую функцию, которая при подстановке значения x будет давать значение y=3x+1.
Для нахождения обратной функции y=3x+1 необходимо преобразовать исходную функцию следующим образом:
- Выразим x через y
- Поменяем местами x и y
После преобразований получим обратную функцию, которая будет иметь вид: f⁻¹(x) = (x-1)/3. Эта функция позволяет нам получить значение x по известному значению y функции y=3x+1.
Обратимость функции y=3x+1 и наличие обратной функции имеет ряд практических применений. Например, она может быть использована для решения уравнений, анализа зависимостей между переменными и т.д.
Вопрос-ответ

Как определить, является ли функция y=3x+1 обратимой?
Функция y=3x+1 является обратимой, так как ее график представляет собой прямую линию, которая не пересекает ось OX. Также, чтобы проверить обратимость, можно применить критерий уравнения f(x) = f(y) => x = y, который в данном случае выполняется.
Каково значение y в функции y=3x+1 при заданном значении x?
Значение y в функции y=3x+1 можно найти, подставив заданное значение x в уравнение и выполнить простые вычисления. Например, для x=2, исходя из уравнения y=3x+1, получим y=3*2+1=7.
Каково значение x в функции y=3x+1 при заданном значении y?
Значение x в функции y=3x+1 можно найти, решив уравнение y=3x+1 относительно x. Например, для y=10, подставляем в уравнение и решаем уравнение 10=3x+1. Вычитаем 1 и делим на 3, получаем x=(10-1)/3=3.
Как изменяется график функции y=3x+1 при изменении значения коэффициента a?
Коэффициент a в уравнении y=3x+1 определяет наклон графика прямой. При увеличении значения a прямая становится круче, а при уменьшении - менее крутой. Если a<0, график будет отражен относительно оси OX.



