В мире, полном разнообразных явлений и процессов, важно уметь анализировать и интерпретировать полученные данные. Одним из ключевых методов при изучении различных явлений является анализ графиков. График – это графическое представление, которое позволяет наглядно увидеть зависимость одной величины от другой. Частота является одной из важнейших характеристик, которую можно получить из графика.
Существуют различные методы и формулы, которые позволяют определить частоту по графику. Один из самых распространенных способов – анализ периодических функций. Периодическая функция – это функция, которая повторяет себя через определенный промежуток времени или координат. Анализ периодических функций позволяет определить периодичность изменения величины и, следовательно, частоту. Для этого необходимо выделить повторяющиеся элементы на графике и применить соответствующие математические формулы.
Основные принципы и подходы при использовании графика для определения частоты
В данном разделе рассмотрим важные аспекты и стратегии, которые используются для определения частоты сигнала при помощи графика. Результаты, полученные с помощью этого подхода, позволяют получить представление о частотных характеристиках и преобразованиях сигнала без использования строгих математических формул, а только на основе визуального анализа графического изображения.
Первый и самый простой способ – это определение частоты сигнала путем измерения периода колебаний на графике. Визуально выделяется участок, наиболее строго повторяющийся и узнаваемый, что позволяет определить период и, следовательно, основную частоту сигнала. Однако, в случае несинусоидального сигнала или наличия шумов, данный метод может быть недостаточно точным и требует дополнительной обработки данных.
Другим подходом является анализ амплитудных модуляций на графике сигнала. Основная идея заключается в выявлении повторяющихся амплитудных пиков и определении периода между ними. Это позволяет вычислить частоту сигнала, поскольку период повторения амплитудных модуляций соответствует промежутку времени между двумя положительными фазами колебаний.
Также можно обратить внимание на изменение фазы сигнала на графике. Фазовые модуляции проявляются путем изменения точки старта колебаний на графике. Путем анализа изменения фазы можно определить частоту сигнала, так как каждое слагаемое соответствует положительной фазе колебаний.
Важным аспектом является также обнаружение гармонических компонентов на графике. Гармонические модуляции – это регулярные колебания с постоянным периодом и амплитудой. Их выявление может помочь в определении частоты сигнала, так как каждая модуляция соответствует определенной частоте, а порядок модуляций определяет количественную характеристику сигнала.
Интерполирование данных и поиск периода: эффективные методы расчета

В данном разделе будут рассмотрены эффективные методы расчета интерполирования данных и поиска периода при анализе графиков. Данный подход позволяет нам более точно определить частоту и синтезировать формулы, основываясь на имеющихся данных.
Интерполирование данных - это процесс приближения значений функции между имеющимися точками, что позволяет заполнить пробелы в данных. Это необходимо для более точного определения частоты и формы графика. За счет использования различных методов, таких как линейная интерполяция, полиномиальная интерполяция и сплайны, можно получить достаточно точную аппроксимацию и предсказывать значения функции внутри заданного диапазона.
Поиск периода - это процесс определения периодически повторяющихся паттернов или циклов в данных. При анализе графиков, поиск периода может быть полезен для определения частоты колебаний или повторяющихся событий. Существуют различные методы для этого, включая корреляционный анализ, преобразование Фурье и автокорреляционную функцию. Эти методы позволяют нам найти периодические закономерности и использовать их для более точного расчета частоты.
Использование эффективных методов интерполирования данных и поиска периода позволяет нам получить более точные результаты при анализе графиков. Это особенно полезно при работе с неполными данными или при наличии шумовой составляющей. В следующих разделах будут рассмотрены конкретные формулы и примеры использования данных методов для расчета частоты по графику.
Анализ спектра сигнала: методы распознавания частот по изменениям формы графической иллюстрации
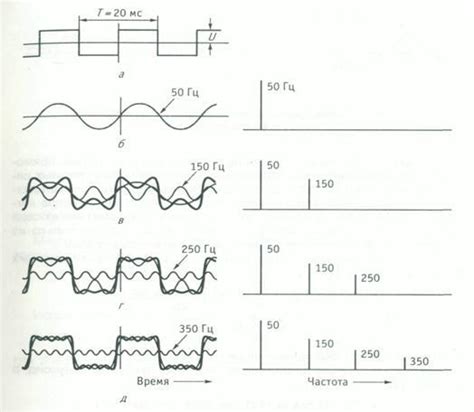
Для анализа спектра сигнала, который может выглядеть как изменение амплитуды, фазы или иных параметров в зависимости от времени или пространственной координаты, используются различные методы. Одним из таких методов является анализ графической иллюстрации сигнала и определение его частотных характеристик.
На практике встречаются разные виды графических представлений сигналов, включая графики временных рядов, спектрограммы, частотные диаграммы и другие. Каждый из таких типов представлений имеет свои особенности, на которые следует обратить внимание при анализе. Например, форма и расположение пиков на спектрограмме могут указывать на определенные спектральные составляющие сигнала и их соответствующие частоты.
Одним из подходов для определения частоты по графику является метод просмотра и оценки пиковой структуры сигнала. Это означает, что мы ищем такие точки на графике, где амплитуда достигает наибольших значений. Иногда пики могут быть острыми и выраженными, что позволяет совершить более точную оценку их положения на оси времени или пространственных координат. Однако в некоторых случаях пики могут быть размытыми и смещенными, что требует аккуратного исследования.
Применение математических моделей: формулы и алгоритмы для точного вычисления частотных характеристик

В данном разделе рассмотрим использование математических моделей для более точного определения частотных характеристик исследуемых явлений. Разберем основные формулы и алгоритмы, позволяющие с высокой точностью определить частоту событий и процессов без непосредственной наблюдаемости или исследования.
Для более точного исследования и определения частоты явлений применяются различные математические модели, которые позволяют предсказать и анализировать данные с большей точностью. Одной из основных формул, используемых при анализе данных, является формула периодических функций, которая позволяет определить периодичность и частоту данных событий.
Кроме того, для более точного определения частоты часто используется алгоритм быстрого преобразования Фурье (БПФ), который позволяет разложить сложную функцию на ряд простых гармонических колебаний. Этот алгоритм основан на математическом методе преобразования временной области в частотную.
Еще одним эффективным алгоритмом для точного определения частоты является метод наименьших квадратов, который позволяет аппроксимировать исследуемые данные кривой и находить периодические колебания. Этот метод основан на минимизации суммы квадратов отклонений между исходными данными и моделью.
Использование математических моделей, формул и алгоритмов позволяет более точно определять частотные характеристики исследуемых явлений, что в свою очередь способствует углубленному анализу данных и получению более надежных результатов. Опираясь на различные математические методы и модели, исследователи и специалисты смогут более точно определить частоту и процессы, что является необходимым для решения ряда научных и практических задач в различных областях.
Вопрос-ответ

Как определить частоту по графику?
Определение частоты по графику осуществляется путем измерения периода колебаний на графике и использования формулы f = 1 / T, где f - частота, а T - период.
Какие способы расчета частоты можно использовать?
Существует несколько способов расчета частоты по графику. Один из них - измерение периода колебаний и использование формулы f = 1 / T. Также можно использовать метод определения частоты по числу колебаний за заданный промежуток времени, применяя формулу f = n / t, где n - количество колебаний, t - время.
Какая формула используется для определения частоты по графику?
Для определения частоты по графику используется формула f = 1 / T, где f - частота, а T - период колебаний. Путем измерения периода на графике и подстановки его значений в формулу можно рассчитать частоту.



