Одной из важнейших областей математики является геометрия. Она изучает фигуры, их свойства и отношения между ними. В геометрии существуют различные понятия и определения, которые помогают нам анализировать и изучать разнообразные геометрические объекты.
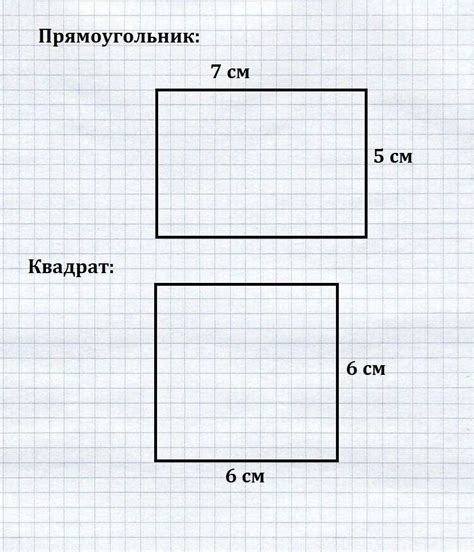
Один из простейших и наиболее распространенных геометрических объектов - прямоугольник. Это фигура с четырьмя прямыми сторонами и углами, у каждого из которых равны по 90 градусов. В геометрии прямоугольнику есть две основные характеристики, которые позволяют определить его размеры и площадь - это периметр и площадь.
Периметр прямоугольника - это сумма длин всех его сторон. Он показывает, сколько надо пройти пути, чтобы обойти фигуру по ее контуру. Периметр является важным понятием, так как он помогает нам определить длину ограждающей линии и позволяет оценить необходимое количество материала для постройки или облицовки прямоугольного объекта.
Площадь прямоугольника - это количество площади, занимаемое данным объектом на плоскости. Для прямоугольника площадь определяется как произведение длин его сторон. Понимание площади помогает нам определить, насколько пространство будет заполнено этим объектом и какие площади могут быть использованы для различных целей, таких как строительство, архитектура или ландшафтный дизайн.
Основные понятия периметра и площади прямоугольника
Периметр прямоугольника является мерой длины его границы и определяется как сумма всех сторон фигуры. Величина периметра позволяет оценить общую длину, которую необходимо пройти, чтобы обойти фигуру вокруг ее границы.
Площадь прямоугольника характеризует площадь внутри границ фигуры и определяется как произведение длины и ширины. Эта величина позволяет оценить количество площади, которую фигура занимает на плоскости.
Обладая понимаем основных понятий периметра и площади прямоугольника, можно проводить различные вычисления и сравнивать разные фигуры, опираясь на эти величины. Кроме того, эти понятия имеют практическое применение в архитектуре, инженерии, строительстве и других областях, где важно оценить размеры и площади различных прямоугольных конструкций.
Основы периметра прямоугольника и его вычисление

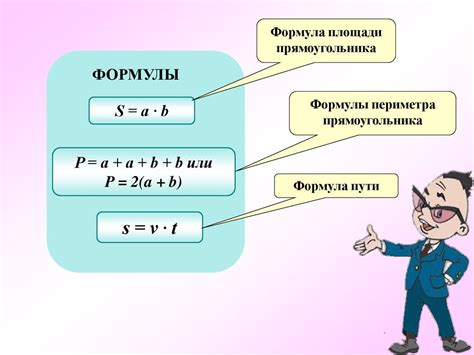
Вычислить периметр прямоугольника можно с помощью простой формулы. Для этого необходимо знать длины двух его сторон – ширины и высоты. Периметр равен удвоенной сумме ширины и высоты, то есть в два раза больше, чем сумма этих значений. Если обозначить ширину как a, а высоту как b, то формула для вычисления периметра будет иметь вид: периметр = 2a + 2b.
Как определить площадь прямоугольника и какие методы использовать?

В данном разделе будут рассмотрены способы определения площади прямоугольника и представлены различные подходы к его вычислению.
Площадь прямоугольника - это показатель, отражающий его площадь поверхности. Площадь прямоугольника можно найти различными способами - с использованием длины его сторон, диагоналей, радиуса описанной окружности или с использованием специальных формул, которые учитывают определенные характеристики прямоугольника.
| Метод | Описание |
|---|---|
| Метод боковых сторон | Вычисление площади прямоугольника по формуле: S = a * b, где a и b - длины его сторон. |
| Метод диагоналей | Вычисление площади прямоугольника по формуле: S = 0.5 * d1 * d2, где d1 и d2 - длины его диагоналей. |
| Метод радиуса окружности | Вычисление площади прямоугольника по формуле: S = R^2, где R - радиус описанной окружности. |
| Метод по формуле Херона | Вычисление площади прямоугольника по формуле: S = sqrt(p * (p - a) * (p - b) * (p - c)), где a, b, c - длины его сторон, p - полупериметр прямоугольника. |
В зависимости от доступных данных и требуемой точности можно выбрать один из методов расчета площади прямоугольника. Они позволяют определить размер его поверхности и использовать полученные значения в дальнейших математических или инженерных расчетах.
Рассчитывайте периметр прямоугольника легко и быстро: формула и подходы расчета
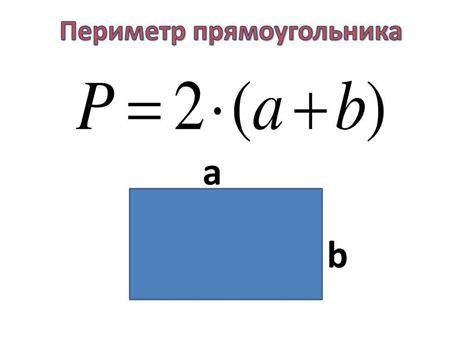
В данном разделе мы обсудим методику определения периметра прямоугольника и представим вам формулы для его расчета. Вы узнаете, как с легкостью определить общую длину всех сторон и применить это знание для нахождения периметра. Мы также поделимся с вами несколькими полезными советами и подходами, которые помогут упростить процесс решения задач на нахождение периметра прямоугольника.
Формула периметра прямоугольника и объяснение каждого элемента
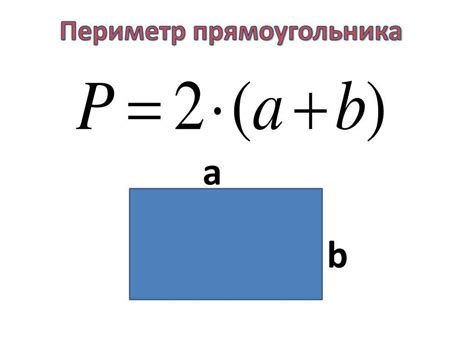
Определим периметр прямоугольника, используя переменные a и b, которые обозначают длины его сторон. Формула для вычисления периметра прямоугольника выглядит следующим образом:
П = 2а + 2b
Здесь 2а означает удвоенную длину одной из сторон прямоугольника, а 2b - удвоенную длину другой стороны. Оба значения складываются, чтобы получить полную длину периметра прямоугольника.
Давайте рассмотрим наглядный пример: у нас есть прямоугольник с длиной стороны a = 5 и шириной стороны b = 3. Применяя формулу, мы можем легко найти периметр прямоугольника. Подставим значения в формулу:
П = 2 * 5 + 2 * 3
Путем вычислений получим:
П = 10 + 6
И окончательный результат будет:
П = 16
Таким образом, периметр прямоугольника с длинной стороны 5 и шириной стороны 3 равен 16.
Практический пример: как найти периметр прямоугольника

Давайте представим себе ситуацию: вы хотите построить забор вокруг своего сада, и вам нужно узнать, сколько кирпичей вам понадобится для этого. Для расчета этой информации необходимо знать периметр прямоугольника, который определит длину всего забора.
Для начала, давайте вспомним, что периметр прямоугольника - это сумма длин всех его сторон. В данном случае, прямоугольник является прямоугольным ограждением вашего сада.
Предположим, что у вас есть прямоугольник со сторонами A и B. Для расчета периметра вам нужно сложить длины всех четырех сторон.
Рассмотрим конкретный пример: возьмем прямоугольник с одной стороной длиной 5 метров и второй стороной длиной 8 метров. Чтобы найти периметр этого прямоугольника, просто сложите длины всех его сторон:
Периметр = сторона A + сторона B + сторона A + сторона B
Периметр = 5м + 8м + 5м + 8м
Периметр = 26м
Таким образом, для постройки забора вокруг сада длиной 5 метров и шириной 8 метров вам потребуется 26 метров кирпичей.
Вычисление площади прямоугольника: методы и формула
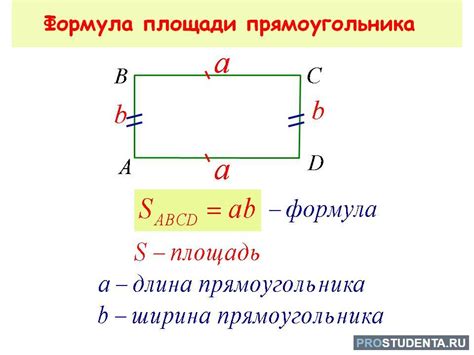
Один из способов вычисления площади прямоугольника - это произведение длины одной из сторон на длину другой стороны. Для этого необходимо знать длины обеих сторон прямоугольника. Например, если длина одной стороны равна a, а длина другой стороны равна b, то площадь прямоугольника можно выразить формулой Площадь = a * b.
Также существует геометрический метод вычисления площади прямоугольника с использованием сетки или таблицы. Для этого прямоугольник разбивается на квадратные ячейки, а затем подсчитывается количество полностью заполненных ячеек внутри фигуры. Площадь прямоугольника будет равна числу заполненных ячеек.
Для вычисления площади прямоугольника можно использовать любой из представленных методов. Они базируются на простых и понятных принципах, позволяющих получить точный результат. Площадь прямоугольника является важной характеристикой этой геометрической фигуры и находит широкое применение в различных сферах жизни и науки.
Как найти площадь прямоугольника с помощью его длины и ширины?

Если вам нужно вычислить площадь прямоугольника, то это можно сделать, зная его длину и ширину. Площадь прямоугольника представляет собой меру его плоскости и показывает, сколько квадратных единиц пространства занимает этот прямоугольник.
Для вычисления площади прямоугольника необходимо умножить его длину на ширину. Это можно записать в виде следующей формулы: площадь = длина × ширина. Или можно использовать синонимы: площадь = длина умножить на ширину, площадь равна произведению длины на ширину.
Например, если у вас есть прямоугольник со сторонами длиной 5 единиц и шириной 3 единицы, то его площадь будет равна 5 умножить на 3, то есть 15 квадратных единиц.
Таким образом, зная длину и ширину прямоугольника, вы можете легко вычислить его площадь, используя простую формулу умножения. Это может быть полезно во множестве ситуаций, где необходимо работать с прямоугольными объектами и определить их площадь.
Интересные примеры применения формулы для вычисления площади прямоугольника
Разнообразные жизненные ситуации и повседневные задачи могут включать в себя расчет площадей прямоугольников. Зная основные принципы формулы, вы сможете применить их во многих интересных сценариях.
Проектирование дома: При разработке плана дома, знание площади каждой комнаты может помочь в определении оптимальной планировки и расстановки мебели. Расчет площадей помещений поможет вам точно определить, сколько квадратных метров нужно для каждого помещения.
Обустройство сада: При планировке ландшафта сада, вам может потребоваться знать площади определенных участков, чтобы рассчитать необходимое количество земли, газона или материалов для озеленения. Красивый участок, созданный на основе расчета площадей, обеспечит гармоничный и эстетически приятный внешний вид.
Укладка плитки: При укладке плитки на пол или стены, важно знать точные площади, чтобы правильно рассчитать количество плиток, необходимых для работы. Это позволит избежать недостатка или излишка материала, а также сэкономит ваше время и усилия при выполнении задачи.
Выбрав примеры из разных сфер жизни, можно увидеть практическую применимость расчета площади прямоугольника. Эти примеры лишь небольшая часть того, как формула площади может быть полезной в реальной жизни.
Вопрос-ответ

Как определить периметр прямоугольника?
Периметр прямоугольника вычисляется по формуле: P = 2(a + b), где a и b - длины сторон прямоугольника.
Как найти площадь прямоугольника?
Площадь прямоугольника определяется по формуле: S = a * b, где a и b - длины сторон прямоугольника.
Можно ли вычислить периметр прямоугольника, если известна только его площадь?
Нет, для вычисления периметра необходимо знать длины сторон прямоугольника, а не только его площадь.
Какие единицы измерения обычно используются для периметра и площади прямоугольника?
Периметр прямоугольника может быть измерен в любых единицах длины (например, сантиметрах, метрах, футах и т.д.), а площадь прямоугольника измеряется в квадратных единицах длины (например, квадратных сантиметрах, квадратных метрах, квадратных футах и т.д.).
Как связаны периметр и площадь прямоугольника?
Периметр и площадь прямоугольника связаны с его сторонами. Периметр определяет длину "внешней границы" прямоугольника, состоящей из всех его сторон, в то время как площадь указывает на количество площади, содержащейся внутри этой границы.



