У каждой плоской фигуры есть свой центр тяжести - точка, в которой сосредоточены все силы, душа и главное "тяжесть" этой фигуры. Она является ключевым фактором в понимании ее равновесия и движения.
Однако, знание координат этого центра тяжести не всегда лежит на поверхности, как и сама плоская фигура. Понять его определение и особенности - это как раскрыть белый свет, который скрыт за прозрачным стеклом.
Путешествие в мир координат центра тяжести плоской фигуры открывает нам широкие перспективы в понимании ее прочности, устойчивости и функциональности. Эти координаты придают логику и основу для дальнейшего изучения разных подвидов этой фигуры и их взаимодействия в пространстве.
Цель знания о центре тяжести плоской фигуры: основные концепции и понятия
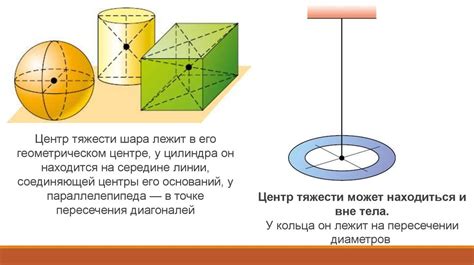
Однако, для понимания сути центра тяжести, необходимо разобраться в ряде базовых понятий и концепций. Во-первых, важно понять, что каждая плоская фигура обладает своим уникальным центром тяжести, который является точкой, в которой можно представить сосредоточенную всю массу фигуры. Во-вторых, следует отметить, что положение центра тяжести внутри плоской фигуры зависит от ее формы, размеров и распределения массы.
Для практического применения знания о центре тяжести плоской фигуры важно уметь определять его координаты с помощью соответствующих формул и алгоритмов. При этом, необходимо учесть, что в случае сложных и неоднородных фигур определение координат центра тяжести может представлять сложности и требовать использования дополнительных методов и приближений.
Расчет геометрического центра и его значение
Расчет геометрического центра обычно осуществляется посредством определения координат. Путем использования математических методов и формул, можно точно определить местоположение этой ключевой точки. Значение координат геометрического центра позволяет оценить распределение массы фигуры и предсказать ее поведение при различных условиях. Чем более сбалансированным будет распределение массы относительно геометрического центра, тем более стабильной и предсказуемой будет поведение фигуры в пространстве.
| Фигура | Значение координат геометрического центра |
|---|---|
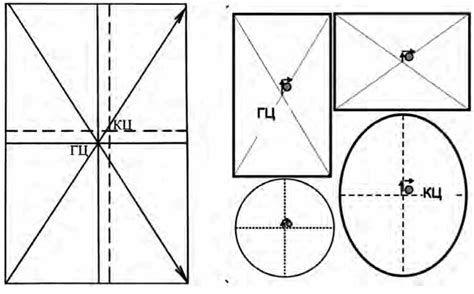
| Прямоугольник | По середине отрезка, соединяющего противоположные углы |
| Круг | В центре фигуры |
| Треугольник | Пересечение медиан |
Способы нахождения средней точки массы двумерных фигур: различные подходы и методы
В данном разделе мы рассмотрим несколько методов, которые позволяют определить среднюю точку массы фигуры на плоскости, пользуясь различными подходами и вычислительными методами. Зная координаты центра тяжести, можно более точно представить распределение массы и провести различные физические анализы или смоделировать поведение объекта.
- Метод шагового разбиения фигуры: данный подход предполагает разбиение области фигуры на небольшие части и последовательное определение массы и центра тяжести каждой из них. Затем из полученных значений вычисляется суммарный центр тяжести фигуры.
- Метод интегральных сумм: этот метод основывается на вычислении определенных интегралов от плотности массы по всей области фигуры. Результатом является вектор центра тяжести, который вычисляется как взвешенная сумма координатных значений интегралов.
- Метод геометрической моделирования: данный подход основывается на создании геометрической модели фигуры и вычислении координат центра тяжести на основе ее геометрических свойств и параметров. Этот метод особенно полезен для сложных или нестандартных фигур.
Каждый из этих подходов имеет свои преимущества и ограничения, и выбор определенного метода зависит от конкретной задачи и доступных вычислительных ресурсов. Но в целом, все они позволяют определить координаты центра тяжести плоской фигуры и использовать эту информацию для более глубокого анализа и моделирования объектов.
Особенности определения центра масс для различных геометрических образов
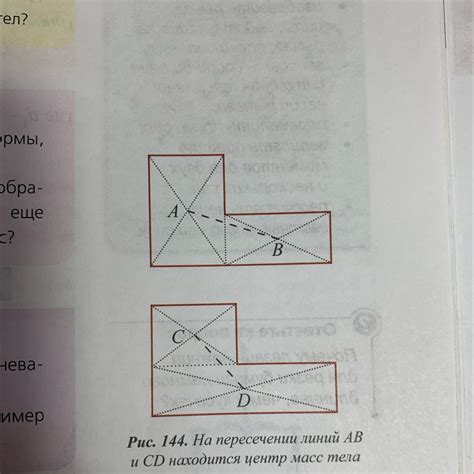
При изучении центра масс различных фигур в двумерном пространстве, возникают определенные особенности, связанные с геометрией и структурой этих фигур. Различные формы и размеры геометрических образов по-разному влияют на определение и расчет их центра масс.
Плоские фигуры с регулярной формой: для таких фигур, включающих квадраты, прямоугольники и круги, определение центра масс относительно площади позволяет использовать симметрию фигуры и геометрические свойства, такие как центр симметрии или радиус-вектор. Это позволяет легко найти координаты центра масс.
Плоские фигуры с нерегулярной формой: такие фигуры, включающие треугольники, многоугольники или нестандартные контуры, требуют более сложных методов расчета центра масс. В этих случаях можно использовать геометрические приемы, такие как разбиение фигуры на простые геометрические элементы, и затем определение центра масс каждого элемента и комбинирование результатов для получения общего центра масс.
Фигуры с полыми или дырчатыми структурами: фигуры такого типа, включающие, например, кольца или внутренние полости, представляют дополнительные сложности при определении центра масс. Здесь важно учитывать не только массу и геометрические свойства внутренних и внешних областей, но также расстояние между ними. Это требует более сложных вычислений и анализа структуры фигуры.
Фигуры с неоднородной плотностью: фигуры, у которых плотность неоднородна, например, материалы с разными плотностями на разных участках, требуют учета этого фактора при определении центра масс. Здесь необходимо учитывать массу каждого элемента фигуры, а также его распределение.
Изучение особенностей определения центра масс различных фигур позволяет лучше понять взаимосвязь геометрии и физики, а также применять эти знания в различных практических областях, таких как строительство, инженерия и дизайн.
Практическое применение понятия геометрического центра в инженерии и архитектуре
- 1. Определение координат центра тяжести позволяет обеспечить равномерное распределение нагрузки на конструкцию. Используя эту информацию, инженеры могут определить оптимальное размещение опорных элементов и грузов, чтобы обеспечить идеальный баланс и предотвратить перекосы или изгибы.
- 2. Понимание координат центра тяжести позволяет инженерам и архитекторам эффективно управлять строительными материалами. Зная точное положение центра тяжести, их могут использовать, чтобы определить, какие материалы будут распределены по площади конструкции, и какие несущие элементы потребуются для обеспечения стабильности.
- 3. Координаты центра тяжести также могут быть использованы для создания более безопасных и устойчивых сооружений. Благодаря точному расчету центра тяжести конструкции, можно предотвратить ее наклон или падение, что особенно важно при проектировании зданий высотной застройки или мостов.
- 4. В области архитектуры, знание координат центра тяжести помогает создавать гармоничные и эстетически привлекательные постройки. Распределение нагрузки и грузов с учетом центра тяжести позволяет создавать легкие и изящные конструкции, которые с легкостью вписываются в окружающую архитектурную среду.
- 5. Конечно, понимание координат центра тяжести также находит практическое применение при проектировании машин и транспортных средств. Расчет и учет центра тяжести позволяет определить идеальное расположение двигателей и других компонентов, чтобы обеспечить стабильность, маневренность и безопасность при движении.
Таким образом, геометрический центр является ключевым понятием, которое имеет важное практическое применение в инженерии и архитектуре. Правильное понимание и использование координат центра тяжести позволяет создавать прочные, безопасные и эстетически привлекательные конструкции, а также эффективно управлять материалами и ресурсами.
Вопрос-ответ

Как определить координаты центра тяжести плоской фигуры?
Для определения координат центра тяжести плоской фигуры необходимо разделить ее на бесконечно малые площадки и вычислить сумму произведений площадей каждой площадки на соответствующие координаты центров этих площадок. Затем эту сумму необходимо разделить на общую площадь фигуры.
Какие особенности существуют при определении координат центра тяжести плоской фигуры?
Особенности определения координат центра тяжести плоской фигуры зависят от ее формы. Для простых фигур, таких как треугольник, прямоугольник или круг, определение координат центра тяжести относительно просто. Однако, для сложных фигур может потребоваться проведение дополнительных расчетов или использование интегралов.
Какие применения есть для координат центра тяжести плоской фигуры?
Координаты центра тяжести плоской фигуры широко используются в различных областях, таких как физика, инженерия и архитектура. Они позволяют определить равновесие фигуры, распределение нагрузки, провести анализ прочности конструкции, оптимизировать дизайн и многое другое.
Как влияют изменения формы плоской фигуры на ее центр тяжести?
Изменения формы плоской фигуры могут существенно влиять на положение ее центра тяжести. При изменении формы фигуры, ее центр тяжести может перемещаться в другое расположение или даже выходить за границы самой фигуры. Поэтому при проектировании конструкций или анализе системы необходимо учитывать эти изменения при определении координат центра тяжести.



