В мире математики существует множество вопросов, требующих глубокого исследования и анализа. Одной из таких проблем является взаимодействие прямой и отрезка на координатной плоскости. Этот вопрос важен не только для математической науки, но и для широкого круга прикладных областей, таких как строительство, картография и компьютерная графика.
Изучение данной проблемы позволяет понять, как прямая и отрезок взаимодействуют друг с другом и как можно определить, пересекаются ли они или нет. Понимание этого позволяет строить не только надежные и точные модели, но и эффективные алгоритмы, использующиеся в реальном мире.
В данном разделе мы рассмотрим один из алгоритмов определения пересечения прямой и отрезка на координатной плоскости. Этот алгоритм основан на использовании геометрических методов, которые помогают нам выявить взаимосвязь между линиями и отрезками на плоскости. Мы изучим ключевые понятия и принципы, которые нужно учесть при разработке алгоритма и реализации его в программном коде.
Пересечение прямой и отрезка: логика алгоритмов
Во многих алгоритмах применяются такие понятия, как углы, наклоны, коэффициенты наклонов, линейные уравнения и пересечения, а также отношения и положения точек на плоскости. Можно выделить несколько основных подходов к решению этой задачи, таких как метод с использованием формулы прямой, графический метод, метод с использованием длин отрезков и сегментов, метод с использованием векторного произведения и метод с использованием угловых отношений.
Важно отметить, что каждый алгоритм имеет свои особенности и ограничения, и выбор конкретного метода зависит от поставленной задачи и условий ее решения. Некоторые алгоритмы позволяют определить только наличие или отсутствие точек пересечения, другие также могут вычислять их координаты. В работе приведено описание и примеры использования различных методов, а также рекомендации по выбору наиболее подходящего алгоритма в зависимости от поставленных задач и требований.
Изучение алгоритмов проверки пересечения прямой и отрезка является важной задачей для решения множества геометрических задач и имеет множество приложений в таких областях, как компьютерная графика, компьютерное зрение, робототехника, геоинформационные системы и др. Понимание логики и принципов работы этих алгоритмов является ключевым для эффективного решения задач, связанных с пересечением прямых и отрезков на плоскости.
Алгоритм Брезенхема: точная и эффективная реализация множественных отрезков на плоскости
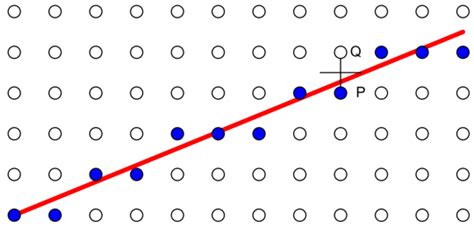
Главная идея метода Брезенхема заключается в том, чтобы использовать приращение координат для определения наиболее близких точек на плоскости. Путем последовательного добавления этих точек можно достичь точного определения пересечения отрезков.
Основной принцип алгоритма Брезенхема состоит в том, чтобы на основании начальной точки отрезка и его конечной точки определить наклон, позволяющий вычислить наиболее близкую точку к исходной. Затем, используя итерационный процесс, полученная точка становится новой начальной, и процесс повторяется до достижения конечной точки.
Этот алгоритм отличается высокой производительностью и точностью, так как допускает только целые значения координат. Он является основой для множества графических приложений и используется при нахождении пересечения линий, построении контуров и определении положения объектов на плоскости.
Метод параболической интерполяции

В этом разделе мы рассмотрим метод параболической интерполяции, который представляет собой эффективный способ приближенного решения задачи определения точки пересечения параболы и отрезка.
Основная идея метода заключается в том, чтобы аппроксимировать заданную функцию параболой, проходящей через три заранее выбранные точки на отрезке. Для этого мы выбираем три точки вблизи искомой точки пересечения и строим параболу, проходящую через эти точки. Затем мы находим точку пересечения параболы и отрезка, используя найденную параболу.
Преимущество метода параболической интерполяции заключается в его точности и скорости. Путем выбора правильных трех точек на отрезке, мы можем получить более точную аппроксимацию параболы и, следовательно, точное значение точки пересечения параболы и отрезка. Кроме того, метод позволяет уменьшить количество итераций, необходимых для нахождения точки пересечения, что приводит к ускорению вычислений.
- Выберите три точки на отрезке.
- Постройте параболу, проходящую через эти три точки.
- Найдите точку пересечения параболы и отрезка.
Использование метода параболической интерполяции может быть полезным при решении задач, связанных с нахождением точек пересечения кривых и линий на координатной плоскости. Благодаря своей точности и эффективности этот метод является важным инструментом для численного анализа и вычислительной математики.
Метод равномерного дискретизирования
Преимущество метода равномерного дискретизирования заключается в том, что он позволяет достаточно точно определить пересечение прямой и отрезка, учитывая особенности их взаиморасположения на плоскости. Использование равномерных отрезков позволяет провести исследование с постоянным шагом и более надежно определить факт пересечения.
В процессе метода равномерного дискретизирования происходит декомпозиция исходного отрезка на равные части. Размеры данных частей подбираются таким образом, чтобы они были достаточно малы для анализа и в то же время позволяли достаточно точно определить состояние каждой части. После разбиения отрезка на равные элементы, производится проверка, находятся ли эти элементы в состоянии пересечения с прямой, а также определение координат точки пересечения при необходимости.
Алгоритм Ву: новый подход к определению точности взаимного пересечения прямой и отрезка
В данном разделе мы рассмотрим инновационный подход к определению точности взаимного пересечения прямой и отрезка на плоскости с помощью алгоритма Ву. Этот алгоритм предлагает новые способы проверки пересечения, используя альтернативные термины и концепции.
Основная идея
Алгоритм Ву основан на принципе, что при определении пересечения прямой и отрезка необходимо учитывать различные факторы и параметры. Он предлагает использовать разнообразные синонимы для описания и оценки пересечения, чтобы подчеркнуть его контекстуальные аспекты и облегчить восприятие информации.
Ключевой особенностью алгоритма Ву является выделение важных элементов их влияния на точность пересечения. Он предлагает использовать такие параметры, как гибкость, точность, степень проникновения и близость к истинному значению, чтобы более точно описать и оценить пересечение прямой и отрезка.
Проникновение используется для описания глубины проникновения прямой внутрь отрезка, а также для определения степени его адаптации к контексту окружающих объектов. Гибкость учитывает возможность приспособления прямой к изменениям вокруг и, следовательно, выражает её способность сохранять пересечение в различных условиях.
В конечном итоге, использование алгоритма Ву позволяет обеспечить более полное и гибкое понимание пересечения прямой и отрезка на координатной плоскости.
Вопрос-ответ

Зачем нужен алгоритм проверки пересечения прямой и отрезка?
Алгоритм проверки пересечения прямой и отрезка используется для определения, существует ли пересечение между заданной прямой и отрезком на координатной плоскости. Это может быть полезно, например, при решении геометрических задач или в компьютерной графике при отрисовке отрезков и прямых.
Как работает алгоритм проверки пересечения прямой и отрезка?
Алгоритм проверки пересечения прямой и отрезка обычно основывается на математическом анализе и геометрии. Он использует уравнение прямой и координаты концов отрезка, чтобы определить, лежат ли они по одну или разные стороны от прямой. Затем проверяется, пересекается ли отрезок с прямой в пределах его концов. Если это так, то прямая и отрезок пересекаются.
Какие данные нужны для работы алгоритма проверки пересечения прямой и отрезка?
Для работы алгоритма проверки пересечения прямой и отрезка необходимо знать координаты двух точек - начала и конца отрезка, а также уравнение прямой. Координаты точек обычно выражаются в виде пар (x, y), а уравнение прямой может быть задано в различных форматах, например, в виде уравнения вида y = ax + b или в параметрической форме.
Какова сложность алгоритма проверки пересечения прямой и отрезка?
Сложность алгоритма проверки пересечения прямой и отрезка зависит от выбранного метода решения. В простейшем случае, используя уравнение прямой и координаты отрезка, сложность алгоритма будет O(1), то есть постоянной. Однако, при использовании более сложных методов, таких как алгоритм Брезенхема или алгоритмы нахождения точек пересечения, сложность может быть выше и зависит от длины отрезка и сложности уравнения прямой.



