Когда мы обращаем внимание на резонансное слово "параллельность", прямо-таки провоцируется наше стремление к пониманию и выяснению действительности данного явления. Само определение этих основополагающих принципов геометрии представляет собой задачу с множеством интересных характеристик.
Разрешите представить вам краткий обзор существенных аспектов изучения параллельности прямых. В этой главе мы проложим путь по исследованию признаков и методов, открывающих перед нами разнообразные способы обнаружения параллельности и измерения между ними с передовыми геометрическими инструментами.
С помощью уникального сочетания теоретического анализа и практических примеров, мы научимся распознавать ключевые признаки параллельности, что ведет нас к осмысленному пониманию ее сути и дальнейшему применению в решении проблем реального мира. Вера в разум всех прямых оказывается полностью оправданной и интуитивной, позволяя выстраивать структуру параллельности с исключительным блеском.
Основные понятия и термины в изучении параллельности прямых
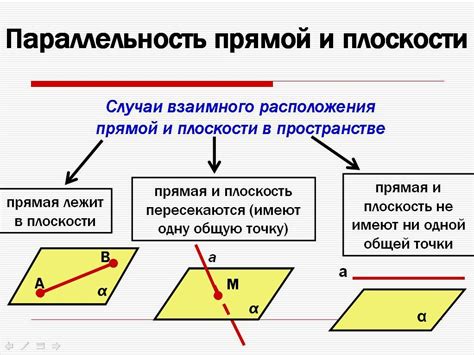
В изучении параллельности прямых существуют определенные основные понятия и термины, которые помогают нам лучше понять данную концепцию. Они представляют собой ключевую составляющую для правильного определения и понимания параллельности прямых.
Термин | Описание |
Медиана | Прямая, которая проходит через точку пересечения двух прямых и делит их на равные отрезки. |
Биссектриса | Прямая, которая делит угол на два равных угла. |
Нормаль | Прямая, перпендикулярная другой прямой. |
Параллельные прямые | Прямые, которые никогда не пересекаются и лежат в одной плоскости. |
Координаты | Числа, которые указывают положение точек на прямой или в плоскости. |
Понимание этих понятий и терминов позволяет нам более глубоко анализировать и определять параллельность прямых. Они служат основой для применения различных методов и признаков, которые позволяют нам идентифицировать параллельные прямые в различных геометрических задачах.
Метод одинакового наклона
Итак, если мы хотим выяснить, являются ли две прямые параллельными, мы можем применить метод равенства коэффициентов наклона. Для этого необходимо рассмотреть уравнения прямых и сравнить их наклоны. Если наклоны обоих прямых одинаковы, то они являются параллельными.
Чтобы применить этот метод, мы должны знать некоторые основные понятия и правила. В алгебраическом представлении прямая задается уравнением вида y = kx + b, где k - коэффициент наклона, а b - свободный член. Коэффициент наклона характеризует наклон прямой. Если у двух прямых коэффициенты наклона равны, то они параллельны.
Метод равенства коэффициентов наклона широко используется в геометрии и алгебре для определения параллельности прямых. Он позволяет упростить задачу, не требуя сложных вычислений или графического изображения прямых. Применение данного метода позволяет с легкостью определить, являются ли прямые параллельными, и таким образом упрощает работу с геометрическими объектами в различных задачах.
| Пример | Уравнение прямой | Коэффициент наклона |
|---|---|---|
| Прямая a | y = 2x + 3 | 2 |
| Прямая b | y = 2x - 1 | 2 |
В данном примере мы имеем две прямые с одинаковым наклоном 2. Следовательно, прямые a и b являются параллельными.
Решение уравнений прямых: секрет ключа к пониманию параллельности
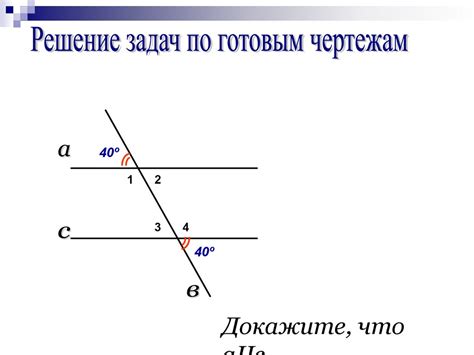
- Если коэффициент наклона для двух прямых равен их однородному значению, то можно утверждать, что эти прямые параллельны. Это связано с тем, что прямые с одинаковым коэффициентом наклона имеют одинаковый угол наклона и, следовательно, никогда не пересекаются.
- Если же коэффициент наклона для двух прямых отличается друг от друга, то прямые пересекаются в точке пересечения, и их углы наклона различны.
Использование углов между прямыми: уникальный подход к определению параллельности

В данном разделе рассмотрим метод, основанный на анализе углов, образованных двумя прямыми. Определение параллельности прямых по углам позволяет не только получить точный результат, но и расширить наши возможности при решении геометрических задач.
Использование углов между прямыми представляет собой интересный подход, который выходит за рамки традиционных признаков параллельности. Вместо простого сравнения угловых коэффициентов или расстояний между прямыми, мы фокусируемся на углах, образованных этими прямыми с третьей прямой или с вектором.
- Один из способов определения параллельности прямых заключается в измерении углов, которые они образуют с одной и той же пересекающей их прямой. Если эти углы оказываются равными или совпадающими, то прямые параллельны.
- Другой метод основывается на измерении угла, который одна из данных прямых образует с некоторым вектором. Если этот угол также равен или совпадает с углом, образованным другой прямой с тем же вектором, то прямые являются параллельными.
Такой подход позволяет в большей степени использовать геометрические свойства углов и векторов для определения параллельности прямых. Благодаря этому методу мы можем детальнее и точнее анализировать геометрические фигуры и решать задачи, связанные с параллельными прямыми.
Схожесть углов наклона линий в геометрии
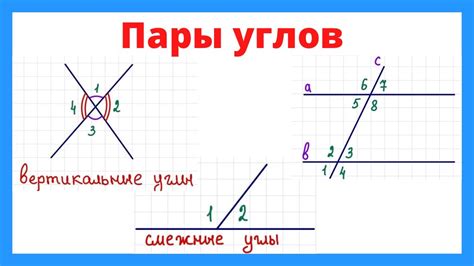
Совпадение углов наклона двух прямых является важным критерием для определения их параллельности. Коэффициент наклона прямой характеризует ее крутизну и показывает, насколько быстро прямая изменяется по горизонтали и вертикали. Если две прямые имеют одинаковый угол наклона, то они будут сохранять пропорцию при перемещении вдоль плоскости. В результате их точки соприкосновения, а также пересечения с другими прямыми, будут находиться на одинаковом расстоянии друг от друга.
Нулевые значения уравнений перпендикулярных прямых
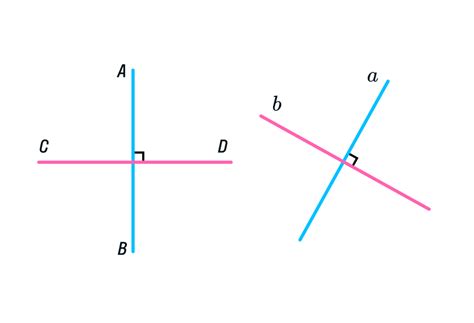
Это означает, что для перпендикулярных прямых существуют особые значения коэффициентов и свободного члена в уравнениях, при которых оба выражения приравниваются к нулю.
Равенство нулю уравнения перпендикулярной прямой связано с тем, что она проходит через точку пересечения двух перпендикулярных прямых.
Соответствие углов между прямыми и их свойствам
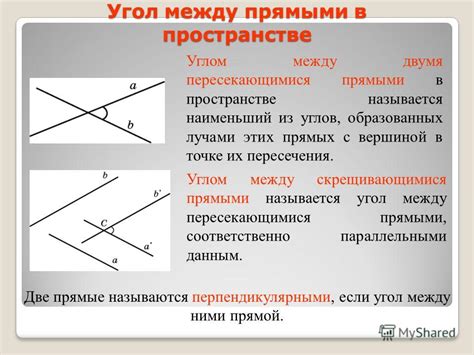
Взаимное расположение прямых может быть определено не только на основе их параллельности, но и на основе соответствия углов, образованных ими. Углы, возникающие в результате пересечения прямых, обладают определенными свойствами, которые могут указывать на параллельность или непараллельность данных прямых.
При анализе соответствия углов следует обратить внимание на их величину и свойства. Один из признаков параллельности прямых - совпадающие углы. Если углы, образованные двумя пересекающимися прямыми и третьей прямой, имеют одинаковые значения, то это может свидетельствовать о параллельности прямых. Однако, следует помнить, что наличие совпадающих углов не всегда означает параллельность, поскольку иные факторы могут влиять на взаимное расположение прямых.
Кроме совпадающих углов, также важно обратить внимание на свойства углов, образованных накрест лежащими прямыми. Если такие углы равны между собой, то это может быть признаком параллельности прямых. При анализе углов следует также учитывать вертикальность прямых, поскольку вертикальные углы всегда равны друг другу.
Вопрос-ответ

Как определить, что две прямые параллельны?
Две прямые считаются параллельными, если они не пересекаются и не сходятся в бесконечности. Если уравнения прямых имеют одинаковые угловые коэффициенты, то это говорит о параллельности данных прямых. Также параллельность прямых можно проверить с помощью построения параллельных линий или с применением специальных математических методов.