Стоит пристально обратить внимание на особенности соединения двух элементов, каждый из которых при своей индивидуальной оценке в равной степени оказывает влияние на общий результат. Деликатно взаимодействуя в своей внутренней структуре, эти непредсказуемые объекты находят общий знаменатель, где одно не может обойти важность другого.
Удачное объединение этих элементов ведет к великим познаниям и оказывает воздействие на каждого, кто принимает участие в их взаимной игре. Одним глазом просматривающий все тонкости этой композиции может уловить тончайшие детали, почувствовать особое колдовство между истоками этих объектов, способных заставить сердце замирать в ожидании неожиданных результатов.
Эта взаимосвязь подчеркивает важность крепкого, взаимно уважительного отношения, которое лежит в основе любого сближения двух скрытых граней. Умение ориентироваться при взаимодействии с неочевидными элементами требует глубокого понимания и гибкости мышления. Только так возможно достижение новых высот и раскрытие потенциала каждого отдельного элемента, которые в итоге смогут провести зрителя сквозь волшебный мир взаимного переходного этапа.
Теория о прямых и лучах: различия и определения
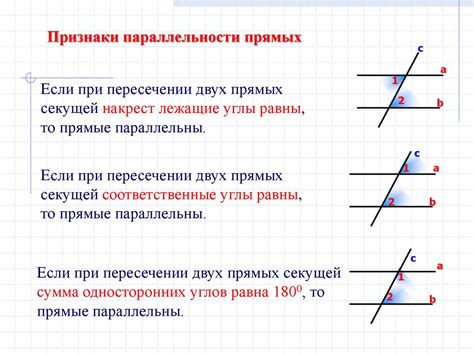
В геометрии существует несколько фундаментальных понятий, относящихся к прямым и лучам. С понятиями прямых и лучей мы сталкиваемся повседневно, но не всегда осознаем различия между ними. Разберемся, как определить прямую и луч и чем они отличаются.
Прямая - это геометрическая фигура, представляющая собой бесконечную последовательность точек, которые лежат на одной прямой линии. Прямая не имеет начала и конца, она можно продлить в обе стороны до бесконечности. Прямая может быть вертикальной, горизонтальной или наклонной.
Например, мы можем представить прямую AB, которая соединяет две точки A и B и продолжается в обе стороны.
Луч - это часть прямой линии, ограниченная одним концом, а другой стороной неограничена. Луч имеет начало, но не имеет конца, он продолжается бесконечно в одном направлении.
Например, мы можем представить луч CD, который начинается в точке C и продолжается дальше в одном направлении.
Таким образом, различие между прямой и лучом заключается в наличии или отсутствии одного из концов. Прямая не имеет начала и конца, тогда как луч имеет начало, но не имеет конца и продолжается бесконечно в одном направлении.
Основополагающие принципы и важные нюансы в рассмотрении пересечения прямых и лучей
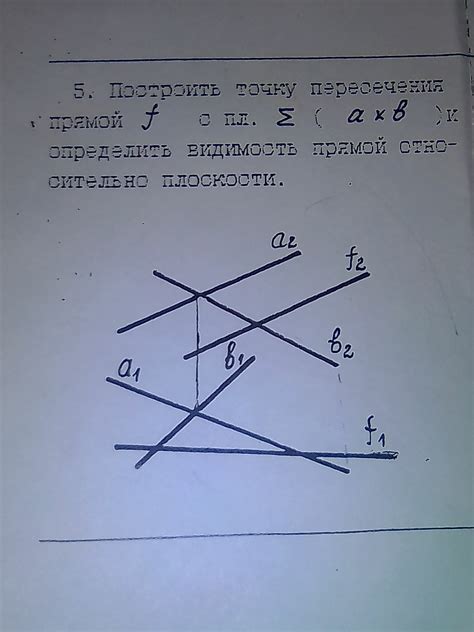
В данном разделе мы поговорим о ключевых принципах и правилах, которые необходимо учесть при исследовании пересечения элементов геометрии. Рассмотрим базовые концепции и важные детали, которые помогут нам разобраться в этой теме.
- Валентные точки и их роль в определении пересечения геометрических объектов.
- Проективные свойства и их влияние на методы исследования пересечений.
- Виды пересечений: точечное, секущее, параллельное, касательное и их особенности.
- Значимость выбора подходящего метода для определения пересечения в каждом конкретном случае.
- Важность учета угловых величин при анализе пересечения геометрических форм.
- Ограничения и особенности в рассмотрении пересечения прямых и лучей.
- Методы объединения и анализа различных типов геометрических объектов.
Усвоение этих принципов и правил позволит вам глубже понять, как осуществляется пересечение прямых и лучей, а также способствует более точному исследованию геометрических фигур в целом.
Существенные отличия между лучом СД и прямой АВ

- Направление: Луч СД имеет одно начальное точечное положение и продолжается бесконечно в указанном направлении. В отличие от этого, прямая АВ не имеет конкретного начала и конца, она простирается бесконечно в обоих направлениях.
- Положение на плоскости: Луч СД всегда находится в одной плоскости и простирается только в этой плоскости. Прямая АВ же может быть либо в одной плоскости с другими объектами, либо параллельна определенной плоскости.
- Взаимосвязь с другими объектами: Луч СД может пересекаться с другими лучами, отрезками, прямыми и плоскостями. Прямая АВ, в свою очередь, может пересекаться только с другими прямыми или занимать их параллельное положение.
- Направление вектора: Луч СД направлен от начальной точки С до бесконечности в указанном направлении. Прямая АВ не имеет направления и может быть равноудалена от двух точек А и В в обе стороны.
Различия между лучом СД и прямой АВ играют важную роль в геометрии и позволяют точно определять положение и направление объектов на плоскости. Понимая эти различия, мы сможем лучше применять соответствующие правила и методы при работе с данными фигурами.
Особенности и характеристики

В этом разделе мы рассмотрим уникальные свойства и особенности, которые сопровождают взаимодействие прямой и луча сд.
Обращаясь к этим особенностям, мы сможем получить глубокое понимание и оценить характеристики этого важного пересечения.
Взаимодействие этих двух элементов предлагает нам различные аспекты, которые должны быть подробно рассмотрены и анализированы.
Одна из ключевых особенностей заключается в способности прямой и луча сд воздействовать друг на друга и влиять на путь своих движений.
Также следует отметить специфические характеристики, которые определяют эффективность и точность процесса пересечения прямой ав и луча сд.
Установление правильной интерпретации этих особенностей и характеристик суммирует наше понимание о взаимодействии прямой и луча сд и нам поможет строить эффективные модели и алгоритмы этого процесса.
Анализ взаимодействия прямой АВ и луча СД в плоскости

Данный раздел статьи посвящен изучению взаимодействия прямой АВ и луча СД в двумерном пространстве. Здесь будет рассмотрено влияние их взаимного пересечения на геометрические свойства и конструкцию плоскости.
Исследование начнем с анализа геометрических особенностей прямой АВ и луча СД. Каждый описываемый объект обладает своими индивидуальными характеристиками, которые определяют его положение и направление в пространстве. Рассмотрим их приближенно, экспериментируя с различными значениями углов и длин отрезков.
- Прямая АВ, в свою очередь, является непрерывным геометрическим объектом, имеющим два различных действительных конца - А и В. При рассмотрении пересечения с лучом СД, необходимо учесть их взаимное положение. Это поможет определить, находятся ли точки А и В по одну сторону от луча СД или же находятся на разных сторонах от него.
- Луч СД представляет собой бесконечную прямую, имеющую исходную точку - С. Отрицательные величины на луче указывают на направление в обратную сторону, когда положительные величины - на направление вперед. При пересечении с прямой АВ возможны различные сценарии, зависящие от величин углов, длин отрезков и их взаимного положения.
Эксперименты и наблюдения, проводимые в данном разделе, позволят установить основные закономерности взаимодействия прямой АВ и луча СД в плоскости. Полученные результаты помогут лучше понять и объяснить геометрические процессы, которые сопровождают пересечение данных объектов.
Далее в статье мы рассмотрим примеры конкретных ситуаций пересечения прямой АВ и луча СД, а также проанализируем их влияние на общую геометрическую картину плоскости. Это позволит лучше осознать важность и роль данных взаимодействий в математике и ее приложениях.
Важно отметить, что существует определенная система правил, навыки и методы, которые позволяют нам точно определить точку пересечения участка луча с данным отрезком. Эти законы и принципы подразумевают собой некую взаимосвязь, в силу которой искомая точка может быть вычислена с необходимой степенью точности и достоверности.
Принципы выявления точек пересечения прямой АВ и луча СД
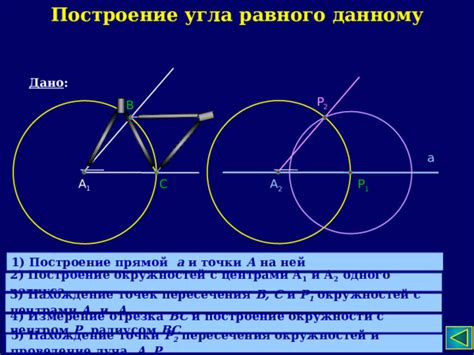
В данном разделе будет рассмотрено описание основных принципов, согласно которым можно определить точку пересечения прямой АВ и луча СД. Без использования специфических терминов, дадим общую идею и подходы к определению этого пересечения.
1. Расчет углов
Первым шагом в определении точки пересечения прямой АВ и луча СД является вычисление углов, образованных этими геометрическими фигурами относительно друг друга. Важно учитывать не только величину угла, но и его направление, что позволяет определить, пересекаются ли они вообще. Для этого используются методы геометрических вычислений и формул.
2. Анализ жесткости линий
Жесткость линий прямой АВ и луча СД играет определенную роль в их пересечении. Если линии представлены как гибкие, плавные кривые, то пересечение может быть неоднозначным и требует дополнительного анализа. В случае, когда линии представлены как прямые, пересечение обычно будет легче определить.
3. Учет особенностей геометрических объектов
Каждая геометрическая фигура имеет свои особенности и характеристики, которые могут оказывать влияние на пересечение с другими фигурами. Например, длина отрезка АВ или угол наклона луча СД. Знание особенностей геометрических объектов позволяет уточнить место пересечения и определить его с большей точностью.
В данном разделе мы рассмотрели принципы, которые лежат в основе определения точки пересечения прямой АВ и луча СД. Расчет углов, анализ жесткости линий и учет особенностей геометрических объектов являются ключевыми элементами процесса определения пересечения.
Анализ и подсчет точек пересечения линии автотрассы и луча движения:
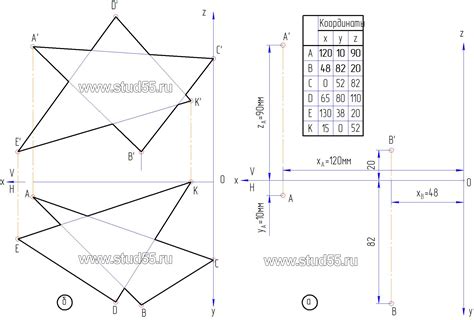
В данном разделе мы сосредоточимся на расчете и различных методах определения точек пересечения линии автотрассы с лучом движения. Методы, которые мы рассмотрим, основаны на анализе геометрических характеристик и использовании математических алгоритмов.
Один из подходов, которые мы рассмотрим, основывается на использовании геометрического анализа и применении теории углов для определения точек пересечения. Мы охарактеризуем этот метод, а также предоставим практические примеры его использования.
Другой метод, который мы рассмотрим, основывается на математическом анализе и использовании координатной плоскости для определения точек пересечения. Мы представим шаги алгоритма, который может быть использован для вычисления точек пересечения, и приведем примеры его применения.
Также мы обсудим возможность использования программного обеспечения, которое может упростить и автоматизировать расчет точек пересечения линии автотрассы и луча движения. Мы рассмотрим различные программные инструменты и их возможности в контексте данной темы.
Наконец, мы представим обзор существующих исследований и их результаты в области расчета и методов определения точек пересечения линии автотрассы и луча движения. Мы проанализируем различные подходы, применяемые в научных работах, и выявим их преимущества и недостатки.
- Методы геометрического анализа точек пересечения;
- Методы математического анализа и использования координатной плоскости;
- Использование программного обеспечения для автоматизации расчета;
- Обзор существующих исследований и их результаты.
Взаимосвязь между показателями углов при пересечении отрезка АВ и направленного сегмента СД

В данном разделе рассмотрим способы определения взаимосвязи между углами, возникающими при пересечении прямой отрезка АВ и направленного сегмента СД. Углы, возникающие в этом контексте, будут исследованы с использованием геометрических методов и специфических соотношений. Рассмотрим основные принципы и правила, которые помогут понять их взаимосвязь.
| Угол | Символ | Описание |
|---|---|---|
| Угол между АВ и СД | α | Угол, образованный прямыми отрезками АВ и СД при их пересечении |
| Угол между АВ и прямой, проходящей через точку пересечения и параллельной СД | β | Угол, образованный прямыми отрезками АВ и прямой, параллельной СД, при их пересечении |
| Угол между АВ и прямой, перпендикулярной СД и проходящей через точку пересечения | γ | Угол, образованный прямыми отрезками АВ и перпендикулярной СД прямой при их пересечении |
Пересечение отрезка АВ и направленного сегмента СД является базовой задачей геометрии, требующей понимания свойств углов, возникающих при данной контекстной ситуации. Рассмотрение взаимосвязи углов α, β и γ позволяет установить связь между углами и определить их взаимное положение и характеристики. Основываясь на рассмотренных правилах и принципах, можно эффективно анализировать и решать задачи, связанные с пересечением прямой АВ и луча СД.
Условия и вариации: разнообразие ситуаций и возможности в пересечении ав и сд

Один из основных факторов, определяющих исход ситуации, - это угол столкновения. Вариации могут быть различными: от прямого пересечения на перекрестке до косого въезда в дорожное движение. В зависимости от направления, угла и скорости движения объектов, водитель принимает соответствующие действия, чтобы избежать аварийных ситуаций.
Другим значимым фактором является показатель интенсивности движения на дороге, который определяет ширину потока автомобилей. От этого параметра зависит способ выбора безаварийной траектории движения. В насыщенных потоках, водителю приходится принимать решения быстро и точно, чтобы избежать столкновения с другими участниками движения.
Немаловажным фактором, непосредственно влияющим на пересечение прямой автомобиля и луча света, являются препятствия, как на дорожной разметке, так и на обочинах. Препятствия могут быть различными: от парковочных автомобилей до больших грузовиков или регулировщика. Угол падения света на препятствие и его отражение могут вызывать определенные трудности для водителя и требовать правильной оценки ситуации.
В данном разделе мы рассмотрели лишь некоторые условия и вариации, которые могут возникать при пересечении прямой автомобиля и луча света. Знание и понимание этих факторов помогает водителям принимать обоснованные решения и совершать безопасные маневры на дороге.
Графическое представление взаимоположения прямой АВ и луча СД
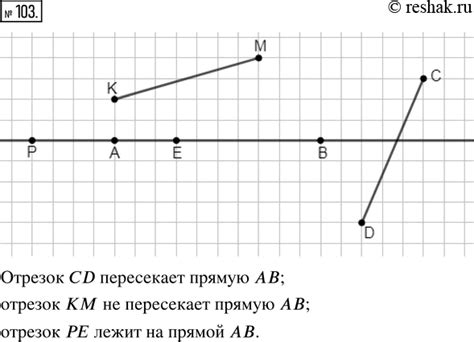
В данном разделе рассмотрим визуальное отображение пересечения отрезка АВ и направленного луча СД на графике с координатной плоскостью.
Для начала, представим отрезок АВ как участок прямой линии между двумя точками А и В, а направленный луч СД как бесконечную прямую линию, исходящую из точки С и проходящую через точку Д.
В графическом представлении отрезок АВ можно представить в виде отрезка линии на плоскости, а направленный луч СД - в виде стрелки, начинающейся в точке С и направленной в сторону точки Д.
Если пересечение прямой АВ и луча СД существует, то графически оно будет представлено в виде точки, значащей точку пересечения данных элементов.
Визуальное отображение пересечения прямой АВ и луча СД может быть полезным при решении геометрических задач, а также в области компьютерной графики и дизайна.
Отображение точек пересечения
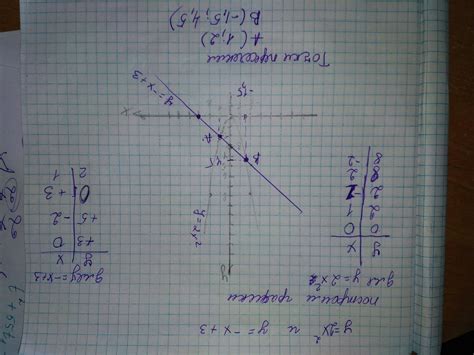
При рассмотрении графического представления точек пересечения важно учитывать, что они могут быть различными: некоторые точки могут быть отмечены явно, а другие могут вычисляться или определяться графически. Часто эти точки обозначаются буквами или символами, чтобы их легко было отличить друг от друга.
Изображение точек пересечения может быть простым или сложным, в зависимости от характера пересечения прямой и луча. Геометрические принципы и правила позволяют определить, как точки пересечения проецируются на графике и как их местоположение влияет на общую картину графика.
Итак, понимание отображения точек пересечения – важный элемент в изучении темы "Пересечение прямой ав и луча сд". Это позволяет наглядно представить взаимное расположение двух линий и определить их точки пересечения на графике. Использование явных обозначений и графических методов анализа позволяет легче воспринимать и анализировать информацию, связанную с пересечением прямой и луча.
Вопрос-ответ

Какие правила и принципы относятся к пересечению прямой ав и луча сд?
Пересечение прямой ав и луча сд регулируется несколькими правилами и принципами. Во-первых, прямая ав должна пересекать луч сд в одной точке. Это означает, что они не должны пересекаться в нескольких или ни одной точке. Во-вторых, прямая ав должна пересекать луч сд только внутри его направления и не должна пересекать его продолжение за его конечной точкой. Наконец, принципом пересечения является применение соответствующих геометрических формул и треугольников, чтобы определить точку пересечения и связанные параметры.
Каким образом определить точку пересечения прямой ав и луча сд?
Определение точки пересечения прямой ав и луча сд может быть выполнено с использованием численных методов или геометрических подходов. Например, можно применить метод подстановки, приравнивая уравнение прямой к уравнению луча и решая систему уравнений. Более геометрический метод включает построение графика прямой и луча на координатной плоскости и определение их точки пересечения графически. Также можно использовать аналитические геометрические формулы, учитывая угловые коэффициенты и начальные точки прямой и луча.
Если прямая ав параллельна лучу сд, есть ли точка пересечения?
Если прямая ав параллельна лучу сд, то точка их пересечения отсутствует. В геометрии параллельные прямые никогда не пересекаются, и то же самое относится и к параллельным лучам. Если прямая и луч параллельны, они продолжат располагаться параллельно друг другу в течение всего своего пути и не найдут общей точки пересечения.
Может ли прямая ав иметь две точки пересечения с лучом сд?
Нет, прямая ав не может иметь две точки пересечения с лучом сд, так как они пересекаются в одной точке. В геометрии две прямые могут пересекаться в одной и только одной точке, если они не параллельны. То же самое справедливо и для прямой и луча - если они пересекаются, то это будет происходить только в одной точке, а не в двух или более.
Как определить точку пересечения прямой ав и луча сд?
Для определения точки пересечения прямой ав и луча сд необходимо решить систему уравнений, составленную из уравнений самой прямой и луча. Первым шагом можно записать уравнение прямой в общем виде и подставить его в уравнение луча. Затем, решив полученную систему, можно определить значения координат точки пересечения.



