В изучении геометрии существует несколько фундаментальных понятий, позволяющих установить связи и сравнения между различными геометрическими фигурами. Одним из таких понятий является подобие, которое позволяет сопоставить разные фигуры и выявить их сходства и различия. Одной из наиболее интересных и важных в геометрии являются треугольники - фигуры, состоящие из трех сторон и трех углов.
Стремясь разобраться во взаимосвязи и сравнительных характеристиках треугольников, необходимо обратить внимание на их составляющие части. Важным элементом каждого треугольника являются его стороны - отрезки, соединяющие вершины треугольника. Сравнение сторон треугольников помогает установить, насколько они похожи или различаются в своей форме и размере.
Анализируя подобные треугольники и их стороны, получаем возможность выявить закономерности и установить математические связи, которые описывают соотношения между сторонами треугольников. Именно эти связи позволяют решать различные геометрические задачи, такие как вычисление значений углов или определение длин сторон, основываясь на данных о подобных фигурах.
Отношения между сторонами аналогичных фигур: аналоги и связь
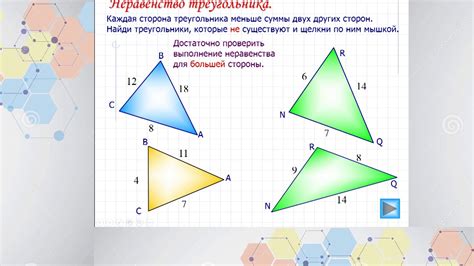
В данном разделе мы рассмотрим взаимосвязь и сопоставление сторон подобных треугольников с целью выявления общих закономерностей и особенностей.
Исследуя аналогичные фигуры, мы можем обнаружить паттерны, которые устанавливают соответствие и способствуют сравнению последовательных сторон. Благодаря такому анализу становится возможным выявить сходства и различия в длине, форме и углах между сторонами разных треугольников.
Применяя синонимы к конкретным терминам, мы можем расширить понимание взаимосвязей между длиной, пропорциональностью, соотношениями и симметрией в контексте отношений сторон подобных треугольников. Это помогает нам углубить наше знание о связи между геометрическими фигурами и взаимодействием их сторон.
Наши исследования позволяют нам выявить закономерности и установить общие правила, которыми руководствуются стороны подобных треугольников. Это позволяет нам не только сравнивать их длины, но и определять значения углов и соотношения длин характеристик треугольников, что открывает перед нами возможности для более глубокого понимания геометрических концепций и их применения в практических задачах.
Раздел: Концепция аналогичных геометрических образов и их элементы
В данном разделе будут рассмотрены основные принципы и понятия, связанные с геометрическими объектами, обладающими сходством в своей форме и структуре. Опираясь на образы, которые выражаются в синонимах для "аналогичных" и "геометрических", мы получаем возможность изучить сущность и взаимосвязи элементов этих образов, придавая им определенные значения и свойства.
Уникальный раздел: Сходство и различия длин сторон в аналогичных треугольниках
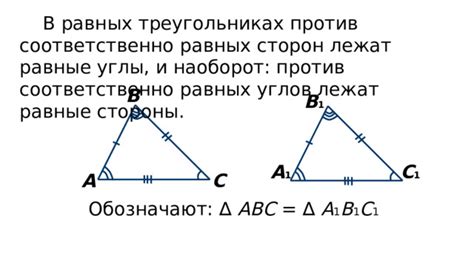
Одной из ключевых особенностей сходства между сторонами в подобных треугольниках является их пропорциональность. В подобных треугольниках соответственные стороны всегда находятся в одной и той же пропорции друг относительно друга. Это означает, что, например, если одна сторона одного треугольника в два раза длиннее другой стороны, то аналогичная сторона в подобном треугольнике будет иметь ту же самую пропорцию.
Однако сходство в длине сторон подобных треугольников не означает полную идентичность. Существуют различные факторы, влияющие на длины сторон, такие как расположение треугольников в пространстве или их ориентация в отношении друг друга. Поэтому, несмотря на пропорциональность, абсолютные значения длин сторон в подобных треугольниках могут различаться.
Также стоит отметить, что сравнение длин сторон в подобных треугольниках может быть полезно для выявления геометрических свойств этих фигур. Например, если в одном треугольнике сторона является кратной длины аналогичной стороны в другом треугольнике, то этот факт может указывать на наличие особых пропорциональных соотношений между сторонами и углами треугольника, таких как соотношение Пифагора или золотого сечения.
Взаимосвязь длин сторон в подобных треугольниках
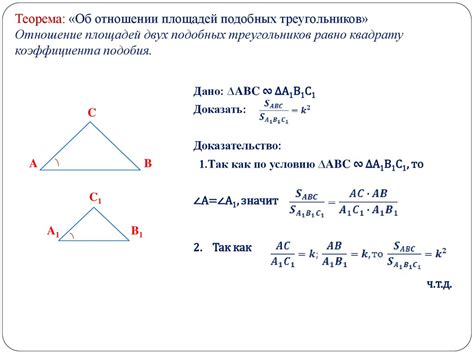
Одна из важных особенностей подобных треугольников заключается в том, что соответствующие стороны пропорциональны. Это значит, что если сторона одного треугольника в некотором отношении соотносится с другой стороной, то эта же пропорция будет сохраняться и между соответствующими сторонами других подобных треугольников.
Например, если в одном треугольнике длина одной стороны в два раза больше длины другой стороны, то в другом подобном треугольнике эти же две стороны также будут соотноситься в том же отношении.
Поэтому, основываясь на знании о пропорциональности сторон в подобных треугольниках, можно вычислять длину одной стороны, зная длину другой стороны и соотношение между ними. Это позволяет упростить решение задач, связанных с нахождением длин сторон треугольников, особенно в случаях, когда одна сторона неизвестна.
Теорема Пифагора и взаимосвязь с подобными треугольниками
Подобные треугольники - это треугольники, у которых соответствующие углы равны, а соответствующие стороны пропорциональны. Важно понимать, что подобные треугольники могут иметь различные размеры, но сохраняют одинаковую форму.
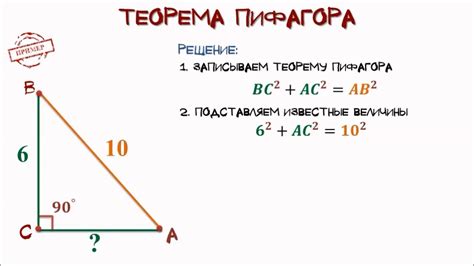
Теорема Пифагора утверждает, что в прямоугольном треугольнике с катетами a и b и гипотенузой c верно следующее соотношение: квадрат длины гипотенузы равен сумме квадратов длин катетов, то есть c² = a² + b².
Связь теоремы Пифагора с подобными треугольниками заключается в том, что когда мы рассматриваем несколько прямоугольных треугольников с разными сторонами, но сохраняющимися пропорциями, теорема Пифагора остается верной. То есть срабатывание теоремы Пифагора при условии, что треугольники подобны, является следствием подобия треугольников и позволяет нам использовать эту теорему для нахождения неизвестных сторон.
Вопрос-ответ

Как определить, являются ли два треугольника подобными?
Чтобы определить, являются ли два треугольника подобными, необходимо проверить, что их углы равны друг другу и их стороны пропорциональны. Если все углы обоих треугольников равны между собой, а соответствующие стороны образуют пропорциональные отношения, то треугольники считаются подобными.
Как можно найти соотношение сторон подобных треугольников?
Для нахождения соотношения сторон подобных треугольников можно использовать свойство пропорциональности. Для этого необходимо взять одну сторону одного треугольника и соответствующую ей сторону другого треугольника, затем сравнить их длины и записать отношение в виде дроби. Повторив этот процесс для каждой стороны, можно получить соотношение всех сторон подобных треугольников.
Как связаны длины сторон и площади подобных треугольников?
Длины сторон и площади подобных треугольников связаны между собой с помощью коэффициента подобия, который является квадратом отношения длин соответствующих сторон. Если длина одной стороны уменьшится или увеличится в n раз, то площадь подобного треугольника уменьшится или увеличится в n^2 раз.
Какие свойства подобных треугольников можно использовать в геометрических вычислениях?
Подобные треугольники имеют ряд полезных свойств, которые можно использовать в геометрических вычислениях. Например, из свойства пропорциональности сторон следует, что для нахождения неизвестной стороны подобного треугольника можно использовать пропорции с уже известными сторонами. Также, зная коэффициент подобия, можно вычислить площадь подобного треугольника по формуле, умножив площадь исходного треугольника на квадрат коэффициента подобия.
Какие еще сходства или различия между подобными треугольниками?
Подобные треугольники имеют сходные геометрические свойства, такие как равные соответствующие углы и пропорциональные стороны. Однако, они могут отличаться размерами и длинами сторон. Также, подобные треугольники могут быть симметричными относительно осей симметрии, которые могут быть горизонтальными, вертикальными или диагональными.



