В современном информационном обществе, где числовые данные одерживают победу, проявляются все новые и новые методы для анализа информации. При изучении и визуализации диаграмм неравенств, особо важно находить точки, ориентируясь на которые, можно получить глубокое понимание состояния данной ситуации. Это позволяет обнаружить скрытую информацию, выявить тенденции и прогнозировать возможные сценарии развития процесса.
В данной статье мы рассмотрим некоторые утонченные методы, которые помогут нам совершенствовать навыки определения точек причерчивания на диаграммах неравенств. Эти методы позволяют нам точно выделить и оценить критические точки, вокруг которых разворачиваются нашисамые главные вопросы и решения.
Чтобы наше путешествие в мир точек причерчивания стало еще более увлекательным и значимым, мы не будем ограничиваться только привычными техниками, а прибегнем к использованию нетривиальных алгоритмов и идей. Эти методы требуют не только глубинного анализа и понимания данных неравенств, но и творческого подхода, нестандартных решений и умения видеть глубже видимого. Великие математики прошлого и настоящего нам показывают, что только креативный подход и новаторство могут привести к открытию сокровенных значений и выдающимся результатам.
Основные понятия и принципы определения пунктирных линий в неравенствах

В данном разделе рассматривается важная тема определения пунктирных линий в неравенствах. Мы выведем основные понятия и принципы, помогающие в этом процессе.
Когда мы сталкиваемся с неравенством, несомненно, возникает необходимость визуализации границы между двумя областями на числовой оси. Для этого используются точки штриховки, которые помогают наглядно представить, в каком направлении искать решение.
Одним из важных понятий является понятие "левой" и "правой" точек штриховки. Левая точка штриховки представляет собой границу, которая является частью решения неравенства, а правая точка штриховки - границу, не входящую в решение и обозначающую его пределы. Это помогает определить, какую область необходимо отметить на числовой оси для нахождения верного решения.
Определение точек штриховки также требует понимания основных принципов. Один из таких принципов - учет направления неравенства. Если неравенство имеет знак "меньше" или "больше", точки штриховки следует проводить на числовой оси соответствующим образом. В случае, когда неравенство имеет знаки "меньше или равно" или "больше или равно", точки штриховки должны быть открытыми, чтобы учесть возможность равенства.
В данном разделе мы ознакомились с основными понятиями и принципами, помогающими определить точки штриховки в неравенствах. Понимание этих ключевых понятий и принципов существенно способствует правильной интерпретации неравенств и нахождению верного решения.
Графический способ выявления шаблонов в неравенствах
В данном разделе представлена графическая методика определения точек штриховки в неравенствах. Этот метод позволяет исследовать взаимное расположение графиков функций и неравенства, выявляя те области, в которых неравенство выполняется. Он основан на визуализации и анализе графиков и предоставляет интуитивно понятную и наглядную картину решения задачи.
Преимуществом графического метода является его универсальность и простота в использовании. Он может быть эффективно применен при решении различных типов неравенств, включая линейные, полиномиальные, рациональные и другие функции. Используя этот метод, возможно определить интервалы, на которых неравенство выполняется или не выполняется, а также выявить точки, где неравенство достигает равенства.
| Шаги графического метода: |
|---|
| 1. Построение графика функции, соответствующей неравенству. |
| 2. Изучение поведения графика функции, выявление его важных особенностей. |
| 3. Анализ графика функции и определение областей, где неравенство выполняется или не выполняется. |
| 4. Выделение точек, в которых неравенство достигает равенства. |
Применение графического метода позволяет увидеть общую картину решения неравенства, а также проверить результаты, полученные с помощью алгебраических методов. Он может быть полезным инструментом, как для изучения теории неравенств, так и для решения практических задач, возникающих при моделировании и оптимизации различных процессов и систем.
Алгебраический метод в определении условной графической области в неравенствах

В данном разделе рассмотрим алгебраический подход к определению точек, образующих условную графическую область в неравенстве. Вместо использования терминов "практические советы" и "определение точек штриховки", мы описываем метод, позволяющий установить положение точек, которые образуют штриховую область в неравенстве.
Алгебраический подход основывается на применении алгебраических методов и приемов для анализа и решения неравенств. Используя алгебру, можно определить множество значений переменной, при которых выполняется данное неравенство. Далее, на основе полученных результатов, можно построить график неравенства и выделить области, которые соответствуют штриховым областям.
Важно отметить, что алгебраический метод предоставляет точные математические инструменты для анализа неравенств и определения условных областей, которые могут быть штрихованы. С помощью алгебры можно проверить различные комбинации значений переменных и найти точки, входящие в условный диапазон. Это обеспечивает более точное и надежное определение точек штриховки в неравенствах.
Сложные неравенства с несколькими переменными: поиск точек пересечения при штриховке
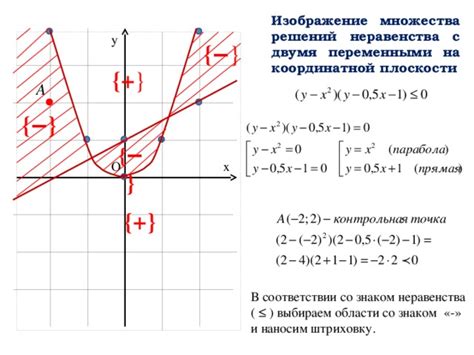
Для начала, важно понимать, что точки штриховки на графиках неравенств представляют собой места, где границы неравенств пересекаются. Они маркируют области, удовлетворяющие всем заданным условиям. В случае сложных неравенств с несколькими переменными, эти точки обозначают области пересечения нескольких ограничений, которые могут иметь различную форму, например, прямые, параболы, окружности и другие кривые.
Для эффективного поиска точек штриховки в сложных неравенствах с несколькими переменными, можно использовать комбинацию аналитических и графических методов. Важно знать, что аналитический подход позволяет найти точные значения координат точек пересечения, а графический метод помогает в визуализации этих точек на графиках.
- Выразите переменные через друг друга, используя заданные неравенства.
- Систематизируйте полученные выражения и приведите их к единому виду.
- Решите полученную систему уравнений, найдя значения переменных, соответствующие точкам пересечения.
- Постройте графики ограничений, указав на них полученные точки пересечения.
При использовании данных методов, важно быть внимательным и последовательным в своих действиях. Также помните, что сложные неравенства требуют более детального и глубокого анализа, поэтому не стесняйтесь проводить дополнительные проверки и перепроверки.
Примеры применения точечных маркеров для решения практических задач

В этом разделе мы рассмотрим несколько интересных примеров, где использование точечной маркировки играет важную роль в решении практических задач. Работа с точками штриховки может быть полезной в упрощении и визуализации неравенств, позволяя наглядно представить различные ситуации и облегчить чертежи.
Первый пример, который мы рассмотрим, связан с определением границы треугольника на координатной плоскости. Используя точки штриховки, мы можем отметить область, в которой лежат точки, удовлетворяющие неравенствам, и таким образом получить графическое представление треугольника.
Другой интересный пример, где точечная маркировка может быть полезной, - это определение области, в которой выполняются условия функции. С помощью точек штриховки мы можем выделить участки графика функции, где значения удовлетворяют определенным ограничениям, и визуально представить это на графическом чертеже.
Один из способов использования точечных маркеров в решении практических задач - это определение области допустимых значений переменных. Мы можем обозначить эту область с использованием точек штриховки и легко определить диапазон, в пределах которого переменные могут принимать свои значения.
Советы по проверке правильности определения точек пунктирной линии в неравенствах
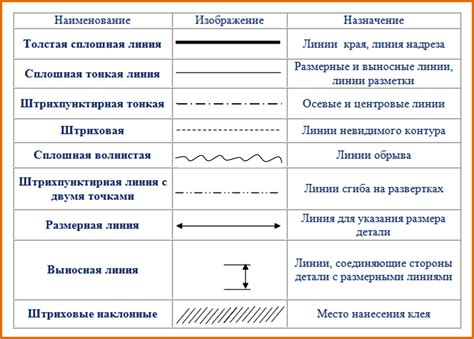
В данном разделе представлены рекомендации и уточнения, которые помогут вам проверить правильность определения точек пунктирной линии в неравенствах. При чтении следующих советов у вас появится ясное представление о том, как правильно определить и проверить корректность этих точек в контексте математических неравенств.
- Определение точек пунктирной линии должно быть основано на точных математических выкладках.
- Важно учитывать все условия, указанные в неравенстве, не пропускать их и не упускать из виду.
- Проверяйте, что указанные точки лежат на графике неравенства и удовлетворяют соответствующим условиям.
- Используйте графическое представление неравенства и визуально убедитесь, что штриховка корректна.
- Не забудьте учитывать направление пунктирной линии при определении точек, исходя из изначального неравенства.
- Внимательно проверяйте все математические выкладки и учтите все приоритеты операций при определении точек пунктирной линии.
- При необходимости, используйте дополнительные математические инструменты и методы для проверки корректности определения точек.
- Не полагайтесь только на интуицию, всегда проверяйте правильность своих выкладок и перепроверяйте полученные результаты.
Следуя этим советам, вы сможете более точно и надежно определять точки пунктирной линии в неравенствах, что позволит вам правильно интерпретировать представленную информацию и применять ее в дальнейших математических вычислениях и рассуждениях.
Методы упрощения неравенств для удобства определения пунктирных точек

Наступает момент, когда необходимо упростить неравенства для целей определения пунктирных точек. В этом разделе мы рассмотрим различные методы, которые помогут вам упростить неравенства, делая процесс определения пунктирных точек более удобным и понятным.
| Метод | Описание |
| Деление неравенств на коэффициенты | Этот метод заключается в делении всех членов неравенства на общий коэффициент, чтобы получить упрощенную форму. В результате этого процесса вы сможете определить пунктирные точки с большей точностью. |
| Перенос всех членов неравенства на одну сторону | Перенос всех членов неравенства на одну сторону делает его более удобным для анализа и определения пунктирных точек. Этот метод позволяет более ясно видеть зависимости между переменными и упрощает последующие шаги. |
| Использование эквивалентных преобразований | Эквивалентные преобразования позволяют упростить неравенства, применив одинаковые операции к каждому члену неравенства. Этот метод поможет вам найти эквивалентную форму неравенства, лучше подходящую для определения пунктирных точек. |
Знание и применение этих методов могут значительно облегчить процесс определения пунктирных точек в неравенствах. Используйте их сообразно заданной ситуации и сделайте процесс более легким и понятным.
Неравенства с параметрами: как определить точки пересечения при изменении переменных
Для начала анализа неравенств с параметрами, требуется установить значения параметров, исследуемых в рамках статьи. После этого проводится исследование формул неравенств и их связь с параметрами. Важно выделить основные ситуации, при которых меняются точки пересечения, и на основе этого провести дальнейший анализ.
| Ситуация | Описание | Методы определения |
|---|---|---|
| Увеличение параметра | Изменение точек пересечения при увеличении значения параметра | Использование методов анализа графиков и алгоритмов приращения |
| Уменьшение параметра | Изменение точек пересечения при уменьшении значения параметра | Анализ алгоритмов убывания и дополнительных условий |
| Множественные параметры | Взаимное влияние нескольких параметров на точки пересечения | Использование математических методов, учет взаимосвязей параметров |
При определении точек пересечения неравенств с параметрами, рекомендуется использовать графические методы, которые позволяют визуализировать изменение точек пересечения при различных значениях переменных. Также необходимо учитывать особенности каждого конкретного неравенства и его связь с параметрами. Правильное определение точек пересечения позволяет более точно определить области выполнения неравенств и провести дальнейший анализ их свойств.
Применение штриховки в экономическом анализе: практические рекомендации

Одним из основных сценариев применения штриховки в экономическом анализе является представление неравенств и отношений между различными переменными. Штриховка позволяет наглядно выделить различные группы данных и увидеть их взаимосвязи.
Важно помнить о правильном выборе типа штриховки, который будет соответствовать поставленным целям анализа. Для этого полезно ознакомиться с различными видами штриховки, такими как горизонтальная, вертикальная, косая или затравочная, и определить, какой из них наиболее эффективно подчеркнет основные моменты вашего экономического анализа.
Еще одной важной рекомендацией является умеренное использование штриховки. Слишком интенсивное использование штриховки может вызвать перегрузку информацией и затруднить восприятие. Поэтому рекомендуется выбирать штриховку с учетом принципа минимализма, чтобы подчеркнуть главные моменты и избежать избыточности.
На практике, рекомендуется также проводить эксперименты с различными вариантами штриховки, чтобы определить наиболее эффективный подход в вашем конкретном экономическом анализе. Сравнение и оценка различных вариантов поможет выбрать наиболее информативный и легко воспринимаемый способ представления данных.
Возможные неточности и ошибки при вычислении точек заштриховки при решении неравенств и способы их учета

Одной из возможных ошибок является неправильная интерпретация неравенства или некорректный выбор условий. Ошибки могут быть связаны с использованием неверного математического знака или неправильным соответствием неравенства с графиком функции. При решении неравенства необходимо внимательно осматривать график и убедиться, что все условия и знаки правильно применяются.
Другая распространенная ошибка - неправильное определение интервалов и точек пересечения. Неверное определение интервалов может привести к тому, что важные точки заштриховки будут упущены. Прежде чем выделять интервалы и определять точки пересечения, необходимо внимательно изучить график функции и учесть все особенности, такие как точки экстремума или точки разрыва.
Также следует обратить внимание на возможные погрешности при вычислении значений функции. Ошибки в вычислениях, связанные с округлением или неправильным подстановками, могут привести к неточным результатам и неправильному определению точек заштриховки. При использовании численных методов решения неравенств важно проверять и контролировать полученные числовые значения, чтобы избежать подобных ошибок.
В целях минимизации возможных неточностей и ошибок в определении точек заштриховки при решении неравенств рекомендуется использовать системы компьютерной алгебры, которые позволяют проводить точные вычисления и предоставляют удобные инструменты для анализа и визуализации графиков функций. Также стоит всегда проверять полученные результаты аналитическими методами для уверенности в правильности определения точек штриховки.
Вопрос-ответ

Как определить точки штриховки в неравенстве?
Для определения точек штриховки в неравенстве нужно найти все значения переменной, при которых неравенство выполняется. Для этого нужно решить неравенство как уравнение и найти корни. Затем, используя тестовую точку на каждом из интервалов между корнями, можно определить, выполняется ли неравенство в данном интервале и соответственно поставить точку штриховки.
Как найти корни неравенства для определения точек штриховки?
Чтобы найти корни неравенства для определения точек штриховки, нужно решить неравенство, как уравнение. Для этого можно привести неравенство к эквивалентному уравнению, заменив знак неравенства на знак равенства и решить получившееся уравнение. Корни уравнения и будут являться значениями переменной при которых неравенство выполняется.
Как использовать тестовые точки для определения выполнения неравенства?
Для использования тестовых точек для определения выполнения неравенства, нужно выбрать значения переменной на каждом из интервалов между корнями неравенства. Затем, подставить выбранное значение в неравенство и проверить выполняется ли оно при данном значении. Если неравенство выполняется, то ставим точку штриховки на соответствующий интервал неравенства. Если неравенство не выполняется, то интервал остается незакрашенным.



