Когда дело касается работы с матрицами, одна из самых важных навыков, которыми должен обладать каждый исследователь или ученый, - умение строить обратную матрицу. Это мощный инструмент, позволяющий решать разнообразные задачи, от решения систем линейных уравнений до анализа сложных теоретических моделей. Однако, похоже, многие сталкиваются с трудностями при попытке построить обратную матрицу самостоятельно. В этой статье мы представим вам полное руководство по построению обратной матрицы шаг за шагом - простыми и понятными для всех способами!
Почему важно понимать обратные матрицы?
В современном мире, где данные и информация занимают центральное место, умение работать с матрицами и их преобразованиями является одним из основных навыков, необходимых в нашем аналитическом сообществе. Обратные матрицы играют важную роль во многих приложениях, будь то решение систем уравнений, нахождение оптимальных решений или алгоритмы машинного обучения.
Однако, концепция обратной матрицы может показаться сложной и запутанной. Именно поэтому мы разработали это уникальное руководство, которое поможет вам понять суть и процесс построения обратной матрицы шаг за шагом - в доступной и понятной форме!
Роль обратной матрицы в линейной алгебре

Обратная матрица оказывается полезной в таких аспектах, как матричная алгебра, решение систем уравнений, определители, линейные пространства и многие другие области линейной алгебры. Она позволяет решать системы линейных уравнений, допускает применение операций сложения, вычитания, контракции и растяжения, а также упрощает многие математические вычисления.
- Обратная матрица может использоваться для обращения линейных преобразований и отображений, что является основой многих прикладных задач в физике, инженерии и информатике.
- Она имеет важную роль в нахождении ранга матрицы и определения ее невырожденности.
- Обратная матрица позволяет моделировать линейные системы и решать их независимо от размерности исходной задачи.
- Она также используется в вычислительных методах и численных алгоритмах, таких как метод Гаусса-Жордана и вычисление обратной матрицы с помощью элементарных преобразований.
Обратная матрица является мощным инструментом, позволяющим эффективно работать с матричными системами и решать разнообразные задачи в линейной алгебре, благодаря своим уникальным свойствам и возможностям.
Основные термины и характеристики обратной матрицы

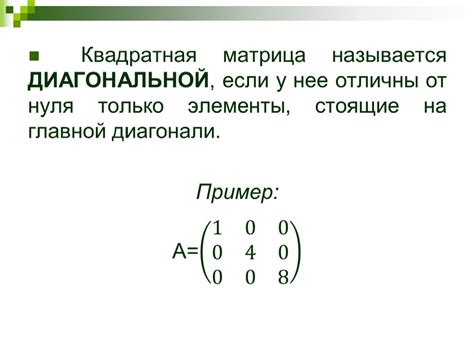
Обратная матрица - это матрица, которая при умножении на исходную матрицу даёт единичную матрицу. Обратная матрица существует только для квадратных матриц, т.к. мы говорим о матрицах размерности n х n.
Определитель - это числовое значение, вычисляемое для квадратной матрицы, которое характеризует её свойства. Определитель обратной матрицы не равен нулю, иначе обратная матрица не существует.
Единичная матрица - это квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные элементы равны нулю. Умножение матрицы на единичную матрицу не меняет исходную матрицу.
Свойство обратной матрицы - при умножении исходной матрицы на её обратную матрицу получается единичная матрица, а при умножении обратной матрицы на исходную матрицу также получается единичная матрица.
Необратимая матрица - это квадратная матрица, у которой определитель равен нулю, и, следовательно, не существует обратной матрицы.
Транспонированная матрица - это матрица, полученная из исходной матрицы путем замены строк на столбцы.
В следующих разделах мы более детально рассмотрим процесс построения обратной матрицы и исследуем её свойства в контексте линейной алгебры.
Методы преобразования для получения обратной матрицы

В данном разделе мы рассмотрим различные методы преобразования матриц, которые позволяют получить обратную матрицу. Для этого мы будем использовать два основных подхода: прямой метод и метод приведения к единичной матрице.
Прямой метод
Прямой метод предполагает применение определенной последовательности операций к исходной матрице с целью преобразовать ее в обратную. В рамках этого метода мы будем использовать различные элементарные преобразования строк, такие как перестановка строк, домножение строки на число и прибавление строки к другой строке. Последовательное применение данных преобразований позволит нам достичь желаемого результата - получения обратной матрицы.
Метод приведения к единичной матрице
Второй подход основан на преобразовании исходной матрицы путем прибавления единичной матрицы к ней слева или справа. Цель данного подхода заключается в том, чтобы привести исходную матрицу к единичной форме, после чего она автоматически становится обратной. Метод приведения к единичной матрице позволяет достичь результата с помощью элементарных преобразований строк, аналогичных тем, которые используются в прямом методе.
Оба метода имеют свои достоинства и ограничения, и выбор между ними зависит от специфики задачи и матрицы, с которой вы работаете. В следующих разделах мы подробно разберем каждый из этих методов и продемонстрируем их применение на практических примерах.
Шаг 1: Определение совместности матрицы
Совместная матрица - матрица, для которой существует обратная матрица. Обратная матрица позволяет решать системы линейных уравнений и выполнять другие математические операции с матрицами.
Противниковая матрица - матрица, которая не имеет обратной матрицы. В случае, если матрица является противоположной, решение системы линейных уравнений становится невозможным.
Для определения совместности матрицы можно использовать различные методы. Один из них - определение детерминанта матрицы. Если детерминант матрицы не равен нулю, то матрица совместна и имеет обратную матрицу.
Продолжение следует...
Шаг 2: Поиск алгебраического дополнения исходной матрицы

Второй этап процесса построения обратной матрицы заключается в нахождении алгебраического дополнения исходной матрицы. На этом шаге мы исследуем каждый элемент исходной матрицы и находим его алгебраическое дополнение, которое понадобится нам в дальнейшем.
Алгебраическое дополнение элемента матрицы образуется путем замены этого элемента на его минор, умноженный на знаковый коэффициент. Минор - это определитель матрицы, полученный из исходной путем вычеркивания строки и столбца, в которых находится данный элемент. Знаковый коэффициент зависит от позиции элемента в матрице и равен умножению -1 на показатель суммы индексов строки и столбца данного элемента.
После нахождения алгебраического дополнения каждого элемента исходной матрицы, мы собираем их в новую матрицу, которая будет служить основой для следующего шага нашего руководства.
- Проходимся по каждому элементу исходной матрицы.
- Вычеркиваем строку и столбец, в которых находится данный элемент.
- Вычисляем минор, полученную матрицу и находим ее определитель.
- Умножаем определитель на знаковый коэффициент.
- Полученное значение является алгебраическим дополнением элемента матрицы.
- Собираем все алгебраические дополнения в новую матрицу.
Шаг 3: Вычисление обратной матрицы с помощью алгебраического дополнения
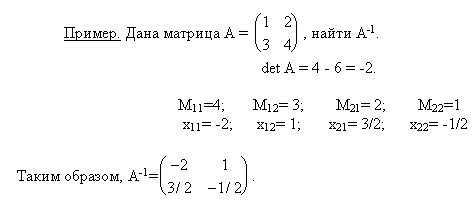
Алгебраическое дополнение - это число, получаемое из элемента матрицы путем умножения его на (-1) в степени суммы номера строки и номера столбца, а затем на определитель матрицы, составленной из оставшихся элементов. Для вычисления обратной матрицы используется определенный алгоритм, который позволяет последовательно вычислить все элементы матрицы-обратной.
Процесс вычисления обратной матрицы через алгебраическое дополнение включает в себя нахождение алгебраических дополнений для каждого элемента исходной матрицы, затем их транспонирование и деление на определитель исходной матрицы. Это позволяет получить обратную матрицу, которая обращает исходную матрицу в операциях умножения, что является важным инструментом для решения различных задач.
Проверка корректности построения обратной матрицы и ее практическое применение

Одним из ключевых шагов в процессе работы с обратной матрицей является проверка корректности ее построения. Данная проверка позволяет убедиться, что каждый этап выполнен верно и что полученная обратная матрица соответствует исходной матрице.
Кроме проверки корректности, обратная матрица имеет множество практических применений в разных областях. Например, она может использоваться в задачах линейной алгебры, численных методах, криптографии, статистике, экономике и других. Обратная матрица позволяет решать системы линейных уравнений, находить обобщенные обратные операторы, производить линейные преобразования, находить обратные значения в определенных формулах и многое другое.
Таким образом, проверка правильности построения обратной матрицы является важным шагом в процессе работы с матрицами, а ее применение имеет широкий спектр возможностей практического использования в различных областях знаний.
Вопрос-ответ

Какую пользу можно получить от построения обратной матрицы?
Построение обратной матрицы позволяет найти решение системы линейных уравнений, а также проводить обратные преобразования в линейных уравнениях с матрицами. Это очень полезно во многих областях, включая линейную алгебру, компьютерную графику, статистику и машинное обучение.
Как проверить, является ли исходная матрица квадратной?
Матрица считается квадратной, если у нее количество строк равно количеству столбцов. Например, матрица размером 3x3 или 4x4 является квадратной, в то время как матрица размером 2x3 не является квадратной.
Как определить, имеет ли исходная матрица обратную?
Матрица имеет обратную, если определитель исходной матрицы не равен нулю. Вычисление определителя матрицы позволяет определить, существует ли для нее обратная. Если определитель равен нулю, то обратной матрицы не существует и матрица называется вырожденной.



