В нашей современной жизни мы часто сталкиваемся с математическими операциями, которые помогают нам лучше понять и анализировать окружающий мир. Одним из таких операций является преобразование дробей.
Дробь - это математический объект, который состоит из числителя и знаменателя, разделенных чертой. Однако, далеко не всегда дробь может быть записана в наиболее простом и удобочитаемом виде. Именно здесь вступает в действие процесс сокращения дробей.
Многие из нас возможно помнят, что в школьные годы нам уже рассказывали о необходимости преобразования дробей в более простую форму. Но все ли мы следуем этому правилу в повседневной жизни? Сокращение дробей - это не только математическое правило, но и способ сделать нашу жизнь проще и удобнее.
Вычислительная точность при упрощении дроби: поиск баланса между точностью и удобством

Основной фактор, влияющий на точность вычислений при сокращении дроби, – это представление значений чисел в памяти компьютера. В современных компьютерах числа обычно представляются в двоичной системе, что может приводить к округлениям и потере точности при выполнении даже самых простых арифметических операций.
При сокращении дроби важно найти баланс между вычислительной точностью и удобством представления результатов. Слишком точные вычисления могут привести к сложному, трудоемкому коду, который трудно будет поддерживать и развивать в дальнейшем. С другой стороны, недостаточно точное сокращение дроби может привести к неточным результатам и ошибкам в последующих вычислениях.
Одним из способов улучшить вычислительную точность при сокращении дроби является использование длинной арифметики, которая позволяет сохранять высокую точность при операциях со значениями с большим количеством знаков. Это может быть особенно полезно при обработке больших чисел или в случаях, когда требуется высокая точность вычислений.
Математические доказательства верности упрощения дроби: важные моменты и советы
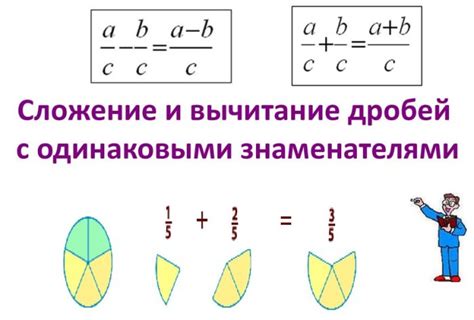
Одним из важных моментов, которые стоит отметить, является то, что правильное сокращение дроби базируется на основных математических принципах и правилах. Доказательство верности упрощения дроби позволяет убедиться в корректности этого процесса и важности его правильного применения.
Для того, чтобы верно сократить дробь и представить ее в наиболее простой и удобной форме, необходимо применить определенные математические операции. Использование таких инструментов, как наибольший общий делитель и деление нацело, позволяет упростить дробь и получить ее наиболее компактное и понятное представление.
Несомненно, для успешного сокращения дробей важно уметь применять эти методы на практике. Четкое понимание математических правил и умение логически рассуждать позволяют достичь верного результата и избежать путаницы. Регулярная тренировка и практика в решении задач с сокращением дробей помогут вам обрести уверенность в своих навыках и добиться успеха в данной области.
Таким образом, изучение математических доказательств правильности сокращения дробей является чрезвычайно полезным и интересным процессом. Правильное применение и понимание этих доказательств поможет вам быть уверенными в том, что вы правильно упрощаете дроби, и позволит вам с легкостью решать задачи на сокращение дробей в будущем.
Влияние упрощения дроби на ее численное значение

В данном разделе рассмотрим, как изменяется числовое значение дроби при ее упрощении. Будем изучать процесс снижения числителя и знаменателя дроби, анализировать влияние этого упрощения на точность представления дроби в виде десятичной дроби и оценивать изменения в численных значениях.
Важно отметить, что упрощение дроби может существенно изменить ее численное значение. При сокращении дроби мы сокращаем оба числителя и знаменателя на их наибольший общий делитель (НОД), что может привести к уменьшению или увеличению числа. Поэтому крайне важно правильно производить упрощение дробей, учитывая их значения и их использование в конкретных контекстах.
Для наглядности, представим численные значения дробей до и после их сокращения в таблице. В таблице будут приведены примеры дробей с различными числителями и знаменателями, а также их численные значения до и после сокращения. Такой подход позволит наглядно продемонстрировать изменения числовых значений при упрощении дробей и оценить их влияние на точность представления дробей в виде десятичных дробей.
| Исходная дробь | Численное значение до сокращения | Численное значение после сокращения |
|---|---|---|
| 2/4 | 0.5 | 0.5 |
| 6/9 | 0.666... | 0.666... |
| 15/75 | 0.2 | 0.2 |
Из приведенных примеров видно, что в некоторых случаях сокращение дроби не влияет на ее численное значение, так как числитель и знаменатель имеют одинаковое значение. Однако, в других случаях сокращение дроби может существенно влиять на ее численное значение и точность представления дроби в виде десятичной дроби. Поэтому необходимо тщательно рассматривать сокращение дроби и учитывать его влияние при проведении вычислений или анализе числовых данных.
Критерии выбора наибольшего общего делителя для удачного сокращения
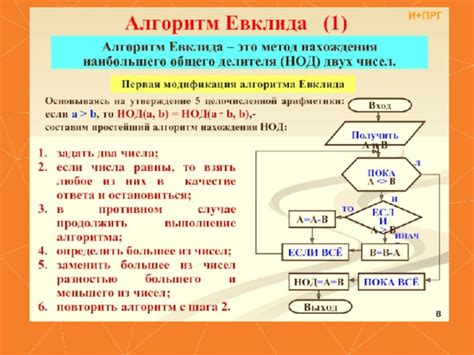
Процесс сокращения дроби требует нахождения наибольшего общего делителя, который позволит получить наиболее простое и удобочитаемое представление. В данном разделе представлены рекомендации по выбору подходящего наибольшего общего делителя для успешного сокращения и получения наиболее компактного варианта.
1. Разложение числителя и знаменателя на простые множители: применение этого метода позволяет определить все простые делители чисел и разложить их на множители. При выборе наибольшего общего делителя следует учитывать, что число должно быть простым и не содержать лишних факторов.
2. Множественное применение простых чисел: для выбора наибольшего общего делителя можно использовать несколько простых чисел, которые являются делителями числителя и знаменателя. Это позволит более точно определить общий делитель и получить более удобное представление дроби.
3. Расчет и сравнение делителей: после разложения числителя и знаменателя на простые множители следует провести расчет и сравнение всех возможных делителей. Рекомендуется выбирать делитель, которому соответствует наибольшая степень в разложении числителя и знаменателя. Такой выбор позволит получить наибольший общий делитель и сократить дробь до наименьшей формы.
- Выбор подходящего наибольшего общего делителя является ключевым этапом в процессе сокращения дроби.
- Чтобы выбрать один наибольший общий делитель, рекомендуется разложить числитель и знаменатель на простые множители.
- Кроме того, можно использовать несколько простых чисел, чтобы тщательно выбрать общий делитель.
- Очень важно провести расчет и сравнение всех возможных делителей для выбора идеального.
Практические примеры сокращения и их анализ

В этом разделе мы представим несколько практических примеров сокращения дробей и проанализируем их особенности. Мы рассмотрим различные варианты манипуляций с числителями и знаменателями, а также оценим результаты этих операций.
Первый пример, который мы рассмотрим, связан с дробью, содержащей множество синонимов для числителя и знаменателя. Мы проведем сокращение дроби, заменив определенные термины на более точные и сократим эту дробь к наиболее простому виду. При этом мы выделим, какие аспекты сущностей имеют наибольшее влияние на результат.
Далее мы рассмотрим пример, связанный с дробью, в которой числитель и знаменатель представлены в виде списков элементов. Мы проведем сокращение дроби, удалив одинаковые элементы из числителя и знаменателя, и определим, как это повлияет на окончательный результат.
Третий пример, который мы рассмотрим, связан с дробью, в которой числитель и знаменатель являются числами с длинной последовательностью цифр и знаков препинания. Мы проведем сокращение дроби, удалив незначащие нули и знаки препинания, и оценим влияние этой операции на полученный результат.
Наконец, мы рассмотрим пример дроби, которая содержит отрицательные значения в числителе и/или знаменателе. Мы проведем сокращение дроби, приведя отрицательные значения к общему знаменателю, и проанализируем изменения, произошедшие в результате.
- Пример с синонимами для числителя и знаменателя
- Пример с списками элементов в числителе и знаменателе
- Пример с дробью, содержащей длинную последовательность цифр и знаков препинания
- Пример с отрицательными значениями в числителе и/или знаменателе
Ошибки, возникающие при неправильном упрощении дробей

При сокращении дробей нередко возникают ошибки, которые могут привести к некорректным результатам. Понимание этих ошибок поможет избежать путаницы и улучшить точность подобных вычислений.
- Неверное определение общих множителей: при попытке сократить дробь могут быть выбраны неправильные общие множители, что приведет к некорректному результату.
- Пропуск сократимых частей: часто происходит пропуск возможности сокращения дроби, что может привести к более сложным и запутанным вычислениям.
- Неправильное сокращение числителя и знаменателя: некоторые сокращаемые части могут быть упущены или неверно выделены, что приведет к некорректному результату.
- Отсутствие проверки на минимальность: некоторые дроби могут быть прокошмарены до уровня, когда их уже нельзя дальше сокращать. Отсутствие такой проверки может привести к лишним вычислениям и потере времени.
- Неучет нейтрального элемента умножения: при сокращении дробей необходимо учитывать, что нейтральным элементом умножения является число 1. Пропуск данного момента может привести к неправильным результатам.
Изучение возможных ошибок, которые могут возникнуть при сокращении дробей, является важным шагом в повышении точности подобных вычислений. Правильное понимание этих ошибок поможет избежать путаницы и обеспечить правильные результаты.
Методы проверки правильного сокращения дробей: важность самопроверки

Здесь представлены несколько методов, которые помогут вам самостоятельно проверить правильность сокращения дробей.
- Метод обратного преобразования. Позволяет проверить полученный результат, обратив его в исходную форму дроби. Если после раскрытия и упрощения исходная дробь совпадает с исходным числом, то сокращение было выполнено правильно.
- Метод сравнения разложений. Отличная возможность проверить правильность сокращения дроби, сравнивая полученную дробь с ее разложением на простые множители. Если оба разложения совпадают, то сокращение было проведено верно.
- Метод проверки на словах. Позволяет проверить результат, выполненный в уме или на бумаге, используя прямую проверку по словам. Этот метод особенно полезен при сокращении дробей с большими числами.
- Метод использования калькулятора. Современные электронные устройства, такие как калькуляторы или программы для работы с дробями, могут быть отличным инструментом для проверки правильности сокращения дробей. Просто введите исходную дробь и сокращенную дробь, и сравните полученные значения.
Убедительная самопроверка важна для контроля правильности сокращения дробей. Используйте эти методы, чтобы быть уверенными в точности ваших результатов и избежать возможных ошибок в вычислениях.
Вопрос-ответ

Зачем сокращать дробь 5/45?
Сокращение дробей позволяет ее представить в наиболее простом виде и упрощает математические операции с ней.
Как правильно сократить дробь 5/45?
Для сокращения дроби 5/45 нужно найти их наибольший общий делитель (НОД), который равен 5. Делим числитель и знаменатель на НОД и получаем дробь 1/9.
Можно ли сократить дробь 5/45 до 5/5?
Нет, дробь 5/45 не может быть сокращена до 5/5, потому что 5 и 45 не имеют общего делителя, кроме самого числа 1.
Что произойдет, если не сокращать дробь 5/45?
Несокращенная дробь 5/45 будет иметь больший числитель и знаменатель, что усложнит проведение математических операций с ней.
Почему дробь 5/45 сокращается до 1/9?
Дробь 5/45 сокращается до 1/9, потому что числитель и знаменатель имеют наибольший общий делитель, равный 5. Деление числителя и знаменателя на НОД дает результат 1/9.



