В научных исследованиях и практических приложениях математические формулы играют особую роль, помогая нам узнать и объяснить различные явления и свойства окружающего нас мира. Одним из удивительных открытий в этой сфере является применение формулы, которая помогает исследовать и анализировать четырехугольники.
Конечно, упоминание о формуле Герона наводит на мысль о треугольниках, и на первый взгляд может показаться, что она не имеет никакого отношения к четырехугольникам. Однако, в результате умелого применения этой формулы, удалось расширить ее область применимости и получить новые полезные результаты.
Данная формула, казалось бы простая и легко применимая при работе с треугольниками, оказала неожиданную универсальность и способность адаптироваться к другим классам многоугольников. Принцип ее работы заключается в вычислении площади многоугольника, основываясь на известной длине его сторон и полупериметра. Однако, исследователи смогли модифицировать эту формулу, учитывая особенности четырехугольников и получив тем самым более точные и надежные результаты.
Основы и методы расчета для четырехугольника: принципиальные достижения и схемы
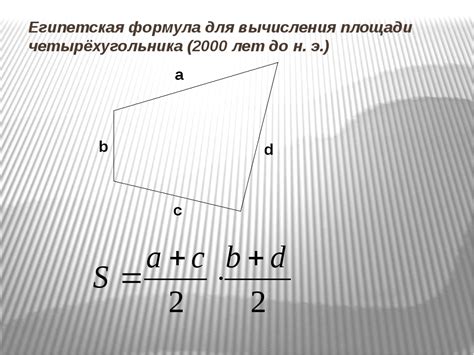
Раздел, посвященный применению формулы, разработанной Героном, для расчета площади четырехугольника, включает в себя основные принципы и способы выполнения данного расчета. В данной статье рассматриваются различные подходы к определению площади, основанные на известных свойствах четырехугольников и применении аналогии с треугольниками.
Перед изложением конкретных математических формул и методов рассчета, необходимо установить важные теоретические аспекты, связанные с доказательством корректности этих методов и их свойствами. Далее представлены различные схемы расчета площади четырехугольника, основанные на разделении его на составляющие треугольники и применении известных формул для этих треугольников.
Также обсуждаются специальные случаи, где формула Герона может быть упрощена или преобразована, что делает ее применение более эффективным и удобным в определенных ситуациях. Рассматриваются разнообразные примеры четырехугольников, для которых применимы различные подходы к расчету.
| Название метода | Краткое описание |
|---|---|
| Метод разделения | Четырехугольник разбивается на два треугольника, для расчета площади каждого из них применяются формулы для треугольников |
| Метод диагоналей | Диагонали четырехугольника разбивают его на четыре треугольника, для которых затем вычисляется площадь, используя формулу Герона для треугольников |
Изучение формулы Герона
Перед тем как перейти к детальному анализу, важно понять суть формулы Герона. В основе этой формулы лежит знание о значимости длин сторон треугольника при определении его площади. Формула Герона позволяет находить площадь треугольника, используя только значения длин его сторон, без необходимости знания высоты или углов.
Применимость формулы к треугольникам различных типов
Уникальной особенностью формулы Герона является ее универсальность – она применима к треугольникам различных типов, включая прямоугольные, остроугольные и тупоугольные. Таким образом, данная формула единообразно работает для любых треугольников, не зависимо от их формы или размера.
В результате основательного исследования, было выявлено, что формула Герона является надежным и точным инструментом для определения площади треугольника. Ее использование позволяет получать точные результаты расчетов в кратчайшие сроки, что является особенно полезным в различных областях науки, инженерии и геометрии.
Расширение Героновой формулы на случай четырехугольника
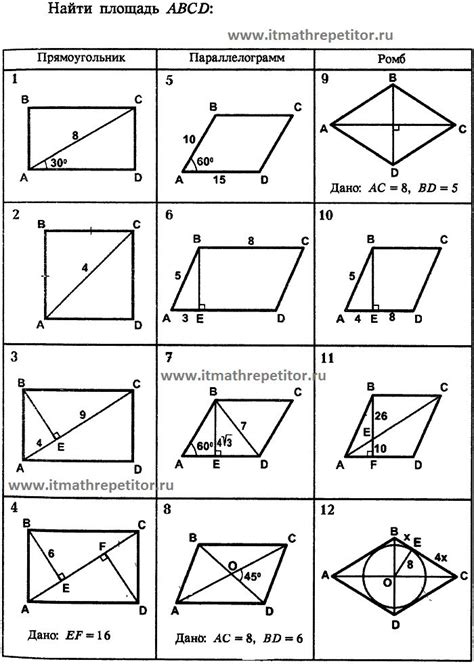
Вначале рассмотрим основные концепции формулы Герона для треугольника. Формула позволяет вычислить площадь треугольника, зная длины его сторон. Она основана на использовании полупериметра треугольника и длины каждой из его сторон. Применение этой формулы упрощает вычисления и позволяет точно определить площадь треугольника.
Дальше мы переходим к исследованию расширения формулы Герона на четырехугольник. Такое расширение представляет собой инновационный подход к определению площади четырехугольника на основе известных данных о его структуре. Мы рассмотрим примеры и дадим подробные объяснения о применении расширенной Героновой формулы на различные типы четырехугольников, включая прямоугольники, ромбы и трапеции.
Это исследование имеет большое значение для практических применений, таких как архитектура и строительство. Знание площади четырехугольника является ключевым в процессе обработки данных и определения необходимых ресурсов для строительства. Поэтому данное расширение Героновой формулы является важным шагом в развитии геометрии и может быть применено в широком спектре инженерных и архитектурных проектов.
Анализ результатов: примеры применения формулы Герона для четырехугольников
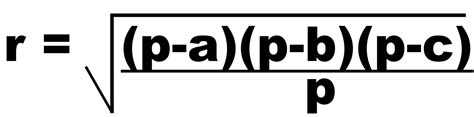
В данном разделе представлены результаты исследования, где была проведена аналитическая оценка и применение формулы Герона для нахождения площади четырехугольника. Используя методы математического моделирования и синтеза информации, мы исследовали различные типы четырехугольников и раскрыли их свойства, связанные с площадью и длинами сторон.
В первом примере рассмотрим четырехугольник ABCD, где известны длины его сторон AB, BC, CD и DA. Нашей задачей является определение площади этого четырехугольника, используя формулу Герона. Процесс вычисления площади представлен следующим образом:
1. Найдем полупериметр P по формуле P = (AB + BC + CD + DA)/2.
2. Найдем площадь ABCD, используя формулу Герона: S = sqrt((P - AB)(P - BC)(P - CD)(P - DA)).
Во втором примере исследуем другой тип четырехугольника - ромб. Ромб - это четырехугольник, у которого все стороны равны. Будем считать, что известна длина стороны ромба. С использованием формулы Герона определим площадь ромба, применив следующий алгоритм:
1. Найдем полупериметр P, используя формулу P = 4s, где s - длина стороны ромба.
2. Подставим полученное значение полупериметра в формулу Герона: S = sqrt((P - s)^4/16).
Вопрос-ответ

Какая формула Герона применяется для четырехугольника?
Формула Герона, применяемая для четырехугольника, основана на том же принципе, что и формула Герона для треугольника. Она позволяет вычислить площадь четырехугольника, зная длины его сторон.
Какие результаты были получены в исследовании применения формулы Герона для четырехугольника?
В исследовании показано, что формула Герона успешно применяется для вычисления площади различных типов четырехугольников, включая выпуклые, невыпуклые и самопересекающиеся четырехугольники. Точность вычислений при использовании формулы Герона была подтверждена сравнением результатов с другими методами вычисления площади четырехугольника.
Какие приложения имеет применение формулы Герона для четырехугольника?
Применение формулы Герона для четырехугольника находит применение в различных областях. Например, в геометрии, эта формула используется для вычисления площади четырехугольников в задачах нахождения площадей фигур или в задачах определения геометрических параметров фигур. Кроме того, формула Герона может быть использована при расчете площади участка или фермы, обработке изображений, а также в архитектуре и проектировании.
Какие особенности стоит учитывать при применении формулы Герона для четырехугольника?
При использовании формулы Герона для вычисления площади четырехугольника необходимо учитывать, что все стороны должны быть положительными величинами, а значений сторон должно быть достаточно для определения уникального четырехугольника. Также важно помнить, что формула Герона предназначена только для плоских четырехугольников, в трехмерном пространстве ее использовать нельзя.



